pldn

CALCULATOARE

PLDN

Cerinte

_ _ _ _

Sa se minimizeze functia : f A+B)(C+D)+BCD

si sa se implementeze cu porti logice de tip SI, SAU, NU, SI-NU, SAU-NU, utilizand un numar minim de porti si circuite integrate.

Aspecte teoretice

Definitia algebrei boolene

O algebra booleana este un ansamblu <M ,·,=> format din

multimea suport M cu un numar finit de elemente, operatia binara

SAU notata cu simbolul +, operatia binara SI notata cu simblolul simbolul · si o relatia de echivalenta intre elementele multimi M notata cu simbolul =, daca sunt indeplinite urmatoarele 6 axiome:

A1 operatiile sunt inchise:

A2 pentru fiecare operatie exista un element neutru:

exista , a.i x + 0 = x

exista , a.i x ·1 = x

A3 operatiile sunt comutative:

x + y = y + x ; x · y = y · x

A4 operatiile sunt distributive:

x + ( y · z) = (x + y) ·(x + z)

x ·( y + z) = (x · y) + (x · z)

A5 pentru fiecare element x .M exista un element x .M :

x + x = x · x = 0

A6 exista cel putin 2 elemente distincte in multimea M:

a.i

Teoreme fundamentale

T1 Legile lui 1 si 0

x · 0 = 0 ; x + 1 = 1

Demonstratie:

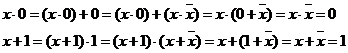
T2 Legile complementului

Demonstratie:

x + 0 = x

, deci Dar

, deci .

A doua relatie se poate demonstra prin dualitate

T3 Legea de unicitate a complementului

exista un singur complement notat prin x

Demonstratie:

Presupunem ca elementul x are 2 complemente x1 si x2

T4 Legile de idempotenta

x + x = x ; x · x = x

Demonstratie:

A doua relatie se poate demonstra prin dualitate

T5 Legile de absorbtie

x + (x · y) = x ; x ·(x + y) = x

Demonstratie:

x + (x · y) = (x · 1) + (x · y) = x 1+ y) = x · 1= x

A doua relatie se poate demonstra prin dualitate

T6 Legea de involutie

Demonstratie:

Prin substitutie , iar

T7 Legile de asociativitate

, (x + y) + z = x + ( y + z) ;

(x · y) · z = x ·( y · z)

Demonstratie:

Notam (x + y) + z = U si x + ( y + z) = V . Se arata ca

U ·V = U si ca U ·V = V . Rezulta U = V .

A doua relatie se poate demonstra prin dualitate

T8 Legile lui DeMorgan

,

Demonstratie:

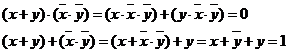
Rezolvare

_ _ _ _

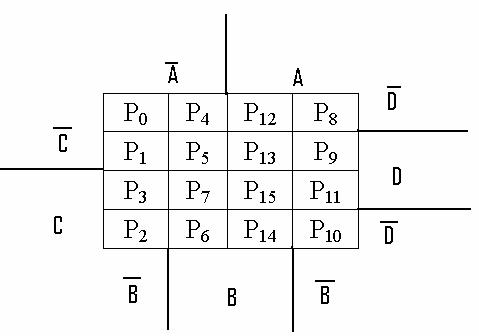
f A+B)(C+D)+BCD

_ _ _ _

f= CD+AD+BD

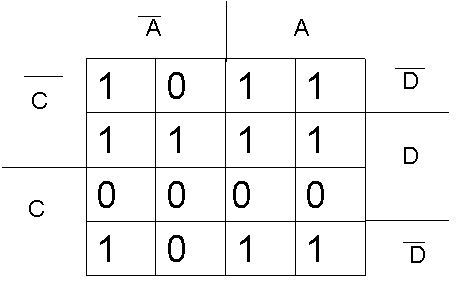
ANEXA

Porti inversoare-3- circuit integrat- 7404

Porti SI-3-circuit integrat-7408

Porti SAU-1-circiut integrat-74HC4075

Bibliografie

Curs-RUSTEM POPA