PROBLEME DE TRANSPORT optimizata si analizata matematic

PROBLEME DE TRANSPORT

In contextul problemelor de optimizare un loc special il ocupa problemele de transport, datorita multiplelor posibilitati de aplicare in diverse sectoare ale activitatii economico-sociale. In cvasitotalitatea activitatilor economice trebuie sa se apeleze la utilizarea unor algoritmi pentru rezolvarea problemelor de transport, deoarece transportul reperelor (produselor) de la furnizori (producatori) la beneficiari (consumatori) cu costuri cat mai reduse (eventual minime) nu poate fi realizat altfel decat facand apel la acesti algoritmi.

1. PROBLEMA STANDARD DE TRANSPORT (BIDIMENSIONALA

Problema standard de transport este intalnita uneori sub denumirea de problema Hitchcock-Koopmans, deoarece a fost enuntata de F.L.Hitchcock in 1941 si completata de Koopmans in 1947.

1.1. FORMULAREA PROBLEMEI

Presupunem ca se dau m centre de productie (producatori) in care exista un anumit produs in cantitatile , produs care trebuie transportat la n centre de consum (consumatori) , necesarul de consum fiind respectiv , iar costul unitar de transport de la centru de productie la centru de consum fiind ; se cere sa se determine un plan optim de transport, adica se cer cantitatile (necunoscute) de produs ce trebuie transportate de la centrul la centrul pentru fiecare pereche de indici .

Se presupune de asemenea ca cererea este egala cu oferta, iar costul transportului este proportional cu cantitatea de produs transportata pe fiecare ruta (,), sau mai scurt notata, .

1.2. MODELUL PROBLEMEI

Problema mai sus formulata se modeleaza astfel:

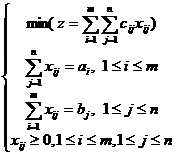(1)

cu conditiile:

. (2)

Observatii: (i). Problema de transport (1) este o veritabila problema de programare liniara sub forma standard. Aceasta are forma 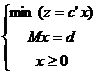(3):

(3)

unde:

;

;

.

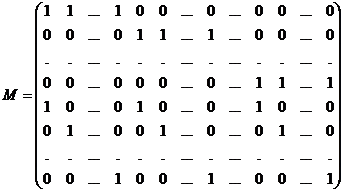Datorita numarului mare de variabile, chiar in cazul problemelor de dimensiuni relativ mici, nu este recomandata utilizarea algoritmului simplex pentru rezolvare, motiv pentru care vom prezenta un algoritm special de rezolvare.

Vom nota cu P multimea programelor problemei (1), adica:

P = }

si cu S multimea programelor optime ale problemei (1), adica:

S =.

(ii). Matricea M are rangul m+n-1.

Intr-adevar, rang(M) si m+nmn daca , deci

rang(M)m+n. Matricea M este de tipul (m+n, mn). Deoarece suma primelor m linii este egala cu suma ultimelor n linii rezulta ca rang(M)m+n-1. Din matricea M se poate forma o matrice patrata nesingulara de ordin m+n-1, daca suprimam linia m+1 si luam din matricea ramasa coloanele 1, n+1, 2n+1, . ,(m-1)n+1, 2, 3, 4, . , n. Produsul elementelor de pe diagonala principala este 1, iar elementele de sub diagonala principala sunt nule.

(iii). Un program de baza al problemei (1) este nedegenerat daca are m+n-1 componente nenule; in caz contrar, deci daca are mai putin de m+n-1 componente nenule este degenerat. Sistemul de valori:

;

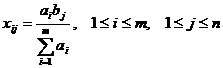este un program al problemei (1), dar nu este program de baza.

(iv). Problema standard de transport poate fi abordata in termenii teoriei digrafurilor, asociindu-i acesteia urmatoarea retea de transport:

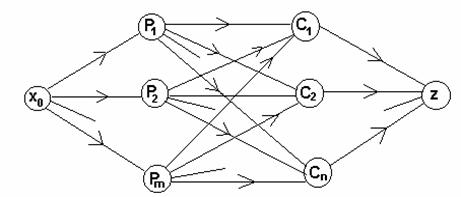
Figura 1.

in care fiecare arc (P_i , C_j) are capacitatea min(a_i, b_j), caz in care rezolvarea problemei de transport se reduce la determinarea fluxului maxim in reteaua de transport asociata, care corespunde cheltuielilor minime de transport.

(v). Analog rezolvarii oricarei probleme de programare matematica, rezolvarea problemei de transport (1) necesita rezolvarea urmatoarelor trei subprobleme:

- determinarea unui program de baza initial (DPBI);

- testarea optimalitatii unui program de baza (TOPB);

- imbunatatirea unui program (in cazul in care nu este optim) (IP).

Daca cele trei subprobleme sunt rezolvate atunci algoritmul de rezolvare pentru problema de transport (1) este urmatorul:

Pasul 1. Se rezolva subproblema DPBI;

Pasul 2. Se rezolva subproblema TOPB;

Pasul 3. Daca programul este optim atunci STOP.

altfel se rezolva subproblema IP; treci la pasul 2.

1.3. METODE PENTRU DETERMINAREA UNUI PROGRAM DE BAZA INITIAL

Exista mai multe metode pentru determinarea unui program de baza initial. Dintre acestea mentionam:

- metoda coltului nord-vest (G. Dantzig);

- metoda costului minim (H. S. Houthakker);

- metoda elementului minim pe linie;

- metoda elementului minim pe coloana;

- metoda diferentelor maxime.

In continuare ne vom ocupa de primele doua metode si recomandam celor interesati utilizarea celei de a doua metode, deoarece aceasta urmareste transportul de produs, cu prioritate, pe rutele cu costuri unitare de transport mici.

Pentru determinarea unui program de baza initial se utilizeaza prezentarea restrictiilor din modelul (1) sub forma unui tabel tabel standard de m+1 linii si n+1 coloane de forma urmatoare:

O pereche de indici , sau cu alte cuvinte, un element (dreptunghi) al tabelului de mai sus va fi numita (numit) celula.

Esenta ambelor metode consta in urmatoarele: se alege o celula (p, q) si se atribuie variabilei x_pq valoarea maxima compatibila cu restrictiile din (1), adica:

.

Sunt posibile trei situatii:

(i). a_p < b_q, caz in care avem , toate celelalte elemente ele liniei p fiind nule, , deoarece disponibilul centrului P_p a fost epuizat. Noua valoare a lui b_p va fi b_p b_p - a_p si se alege o noua celula din zona necompletata a tabelului cu care se procedeaza la fel, pana cand tabelul este complet. Datorita conditiei (2) epuizarea disponibilului producatorilor si satisfacerea solicitarilor consumatorilor sunt simultane.

(ii). b_q < a_p, deci , , solicitarea consumatorului C_q fiind satisfacuta, iar disponibilul in centrul P_p fiind a_p a_p-b_q

(iii). a_p = b_q, deci , , . In acest caz se obtine un program degenerat. Deseori daca se suprima linia p se inlocuieste b_q cu b_q+e noul b_q fiind b_q (b_q+e)-b_q e iar daca se suprima coloana q se inlocuieste a_p cu a_p+e noul a_p fiind a_p a_p+e a_p e

In fiecare din cele trei situatii programul obtinut este program de baza.

Ceea ce diferentiaza cele doua metode este celula cu care incepe determinarea valorilor variabilelor de baza si apoi celula cu care se continua algoritmul de determinare a valorilor variabilelor de baza, dupa ce o valoare a fost determinata. In metoda coltului nord-vest se incepe cu celula (1, 1) situata in coltul nord-vest al tabelului si se continua cu celula situata in coltul nord-vest al tabelului necompletat, in timp ce la metoda costului minim se incepe cu determinarea valorii variabilei de baza corespunzatoare costului minim din matricea costurilor unitare de transport si se continua cu celula corespunzatoare costului minim din tabelul necompletat.

1. TESTAREA OPTIMALITATII UNUI PROGRAM DE BAZA

Pentru testarea optimalitatii unui program al problemei de transport se face apel la teorema Kuhn-Tucker pentru problema de programare liniara, care furnizeaza conditii necesare si suficiente pentru optimalitatea unui program.

Problema duala problemei de transport (1) este problema 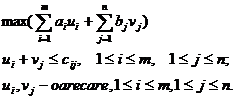(4).

(4)

Cuplul de programe duale si pentru cuplul de probleme de programare liniara duale (1)-(4) este optim daca si numai daca sunt satisfacute conditiile (5).

(5)

Observatie. Din ultimul grup de relatii Kuhn-Tucker din (5) rezulta ca:

.

Daca este un program al problemei (1) atunci primele trei grupe de relatii din (4) sunt indeplinite. Notand prin:

rezulta ca:

,

iar conditia de optim a programului devine:

Algoritmul pentru testarea optimalitatii unui program este urmatorul:

Pasul 1. Se determina multimea ;

Pasul 2. Se rezolva sistemul (cel putin o variabila are valoare fixata);

Pasul 3. Se calculeaza valorile: ;

Pasul Daca atunci scrie programul este optim

altfel rezolva subproblema (IP).

1.5. IMBUNATATIREA UNUI PROGRAM

Pentru imbunatatirea unui program utilizam conceptul de ciclu in tabelul asociat acestei subprobleme, care este tabelul obtinut din tabelul utilizat pentru determinarea unui program de baza din care se suprima ultima linie si ultima coloana, deci din tabelul de forma:

Definim ciclul ca fiind succesiunea de celule (din tabelul precedent) avand una din urmatoarele forme:

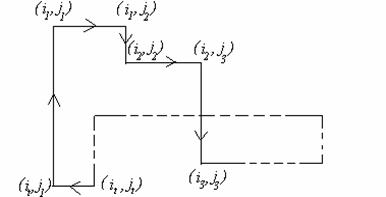
sau

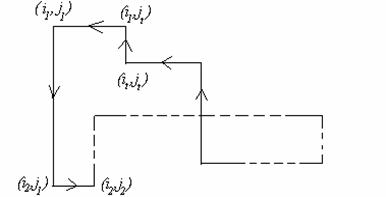
Conceptul de ciclu este esential pentru determinarea celulei care intra in baza si a celei care paraseste baza. Analog criteriului de intrare in baza de la algoritmul simplex, de aceasta data se determina celula corespunzatoare "celei mai pozitive diferente" , care in cazul de fata corespunde celulei (k, l) situata in ciclu pe pozitia (i₁, j₁). Variabila x_kl devine variabila de baza (in celula (k, l) se va transporta produs in vederea imbunatatirii programului), produs ce poate proveni din celulele din ciclu situate pe pozitii pare, presupunand ca numerotarea celulelor se face incepand cu celula (k, l), indiferent daca parcurgem ciclul pornind pe linie sau pe coloana. Pentru a ramane in multimea P a programelor este posibil sa transportam cel mult cantitatea:

.

Cu acestea algoritmul pentru rezolvarea subproblemei (IP) este urmatorul:

Pasul 1. Se calculeaza ;

Pasul 2. Se determina ciclul format din celula (k, l) si alte celule corespunzatoare variabilelor de baza;

Pasul 3. Se numeroteaza celulele ciclului incepand cu celula (k, l);

Pasul Se determina valoarea variabilei x_pq, adica valoarea ;

Pasul 5. Se modifica valorile variabilelor ciclului astfel:

.

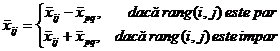Pasul 6. STOP.

Observatii. (i). Noul program de baza este constituit din variabilele bazei precedente (cu valorile variabilelor de baza modificate pentru celulele ciclului) cu exceptia variabilei x_pq care paraseste baza, la care se adauga variabila .

(ii). In cazul in care, in cadrul unei iteratii, si alte valori ale variabilelor de baza (in afara de ) sunt nule, noul program este degenerat.

(iii). Daca x^* este un program de baza al problemei de transport, iar este programul care se obtine din x* prin intrarea in baza a variabilei x_pq, relatia dintre valorile functiilor obiectiv pentru aceste programe este:

,

unde:

.

(iv). Conditia (2) nu restrange generalitatea problemei de transport; daca aceasta este o inegalitate, adica are forma:

, (2')

ceea ce exprima faptul ca cererea totala este mai mare decat disponibilul total si corespunde modelului:

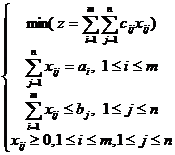(1')

care se poate reduce la modelul standard, introducand un centru de productie fictiv P_m+1, caruia i se atribuie un disponibil egal cu excedentul cererii fata de oferta, adica:

.

Costurile , asociate variabilelor x_m+1,j, pot fi nule sau egale cu penalizarile centrelor de consum in cazul nesatisfacerii cererii.

Analog se standardizeaza problema de transport:

(1'')

care se poate reduce la modelul standard, introducand un centru de consum fictiv C_n+1, caruia i se atribuie un consum egal cu excedentul ofertei fata de cerere, adica:

.

Costurile , asociate variabilelor x_i,n+1, pot fi nule sau egale cu cheltuielile de depozitare (stocaj) in centrele de productie .

2. PROBLEME GENERALIZATE DE TRANSPORT

Prezentam in continuare cateva dintre cele mai reprezentative generalizari ale problemei de transport, mentionand de fiecare data aspectele deosebite pe care le ridica rezolvarea celor trei subprobleme mentionate mai sus si care le disting de problema standard.

2.1. PPOBLEMA DE TRANSPORT CU CENTRE INTERMEDIARE

Presupunem ca produsele realizate de producatori in cantitatile respectiv, sunt transportate la depozite de capacitati , produse ce urmeaza a fi transportate la consumatori , care solicita cantitatile , respectiv.

Daca sunt costurile de transport ale unei unitati de produs de la la , iar sunt costurile unitare de transport de la la se cere sa se determine un plan optim de transport, adica valorile necunoscutelor ce reprezinta cantitatile de produs ce urmeaza a fi transportate de la producatorii la depozitele si ale necunoscutelor ce reprezinta cantitatile de produs ce urmeaza a fi transportate de la depozitele la consumatorii .

Modelul problemei formulate este:

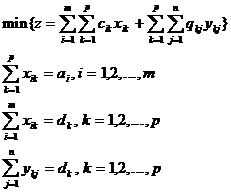(6)

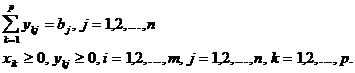
Modelul (6) este echivalent cu doua modele de tipul (1) si admite solutii in ipoteza ca sunt satisfacute conditiile:

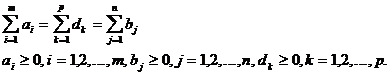(7)

Cele doua modele echivalente cu modelul (6) sunt (8) si (9).

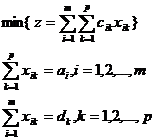(8)

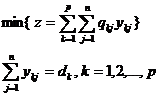(9)

2.2. PROBLEMA DE TRANSPORT CU CAPACITATI LIMITATE

In multe situatii economice concrete capacitatile rutelor de transport sunt limitate, limitarile fiind impuse din diverse considerente tehnico-economice.

Modelul unei asemenea probleme este urmatorul:

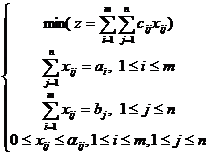(10) Echivalentul relatiei (2) care asigura existenta programelor pentru problema (10) sunt, de aceasta data, relatiile (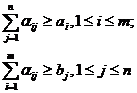11):

(11)

In acest caz subproblemele DPBI si TOPB comporta modificari, in timp ce subproblema IP ramane neschimbata.

Subproblema DPBI consta in atribuirea variabilei x_pq a valorii cu mentiunea ca variabila x_pq este considerata variabila de baza numai in cazul in care sau .

Datorita restrictiilor este posibil ca vectorul sa nu fie program, deoarece este posibil ca disponibilul de produs sa nu fie complet epuizat, sau necesarul de produs sa nu fie complet satisfacut. Se poate arata ca in conditiile (7) pornind de la programul se poate determina un program de baza. Presupunem ca in centrul de productie P_k a ramas neexpediata cantitatea de produs K, iar in centrele de consum C_h si C_l sunt necesare cantitatile H respectiv L. Deoarece cererea este egala cu oferta rezulta ca K = H + L.

2.3. MODELE TRIDIMENSIONALE DE TRANSPORT

Problemele de organizare optima a transporturilor necesare pentru aprovizionarea consumatorilor cu mai multe produse diferite conduc la modele matematice ale caror variabile sunt marcate cu trei indici. Presupunem ca producatorii dispun de produsele , solicitate de consumatorii . Daca se cunosc cantitatile:

cantitatea totala de produse expediate de producatorul

, consumatorului ;

cantitatea de produse , necesare consumatorului ;

cantitatea de produse , disponibile la producatorul ;

si se noteaza cu:

costul transportului unei unitati de produs de la producatorul la consumatorul ;

cantitatea din produsul primita de consumatorul de la producatorul ; modelul standard al problemei de transport tridimensionale este urmatorul:

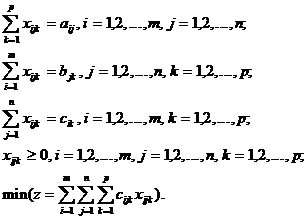(12)

Problema de transport al carei model este (12) admite programe daca sunt indeplinite conditiile (13):

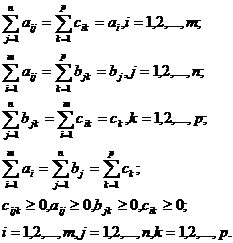(13)