 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Termenul algoritm isi are sorgintea in numele autorului persan Abu Ja'far Mohamed Ibn Musa Al Khowarismi care in anul 825 i.e.n. a redactat un tratat de matematica in care prezenta pentru prima data metode de rezolvare generice pentru anumite categorii de probleme.
In activitatea de programare vom conveni ca prin algoritm sa intelegem o 'modalitate de rezolvare a unei probleme utilizand un sistem de calcul'
Un algoritm este de fapt o metoda sau o reteta pentru a obtine un rezultat dorit.
Un algoritm consta din:
Un set de date initiale care abstractizeaza contextul problemei de rezolvat
Un set de relatii de transformare care sunt operate pe baza unor reguli al caror continut si a caror succesiune reprezinta insasi substanta algoritmului
Un set de rezultate preconizate sau informatii finale, care se obtin trecand de regula printr-un sir de informatii (rezultate) intermediare.
Un algoritm se bucura de urmatoarele proprietati:
(1) Generalitate - un algoritm nu rezolva doar o anume problema ci o clasa generica de probleme de acelasi tip;
(2) Finitudine - informatia finala se obtine din cea initiala trecand printr-un numar finit de transformari;
(3) Unicitate - transformarile si ordinea in care ele se aplica sunt univoc determinate de regulile algoritmului. Ori de cate ori se aplica acelasi algoritm asupra aceluiasi set de date initiale se obtin aceleasi rezultate.
Scopul capitolului analiza performantei algoritmilor.
La ce serveste analiza algoritmilor ?
(1) Permite precizarea predictiva a comportamentului algoritmului;
(2) Prin analiza pot fi comparati diferiti algoritmi si poate fi astfel ierarhizata experienta si indemanarea diversilor producatori [HS78].
Analiza algoritmilor se bazeaza de regula pe doua ipoteze
(1) Sistemele de calcul sunt considerate conventionale adica ele executa cate o singura instructie la un moment dat
(2) Timpul total de executie al algoritmului rezulta din insumarea timpilor instructiilor individuale componente.
Desigur aceasta ipoteza nu este valabila la sistemele de calcul paralelele si distribuite.
In astfel de cazuri aprecierea performantelor se realizeaza de regula prin masuratori experimentale si metode statistice.
In general, analiza unui algoritm se desfasoara in doua etape:
(1) Analiza apriorica
Consta in aprecierea din punct de vedere temporal a operatiilor care se utilizeaza si a costului lor relativ.
Conduce de regula la stabilirea expresiei unei functii care margineste timpul de executie al algoritmului
(2) Testul ulterior
Consta in stabilirea unui numar suficient de seturi de date initiale care sa acopere practic toate posibilitatile de comportament ale algoritmului
Testarea comportamentul algoritmului pentru fiecare set in parte
Se finalizeaza prin culegerea unor date in baza carora pot fi elaborate o serie de statistici referitoare la consumul de timp specific executiei algoritmului in cauza (profilul algoritmului).
Concluzie
Analiza apriorica are drept scop principal determinarea teoretica a ordinului de marime al timpului de executie al unui algoritm
Testul ulterior are ca scop principal determinarea efectiva a acestui ordin prin stabilirea profilului algoritmului
Notatia O desemneaza marginea asimptotica superioara a unei functii. Pentru o functie data g(n), se defineste O(g(n)) ca si multimea de functii:
O(g(n)) = [3.a]
Notatia O se utilizeaza pentru a desemna o margine superioara a unei functii in interiorul unui factor constant.
Pentru toate valorile n superioare lui n0 , valoarea functiei f(n) este pe sau dedesubtul lui g(n) (fig.3.b ).
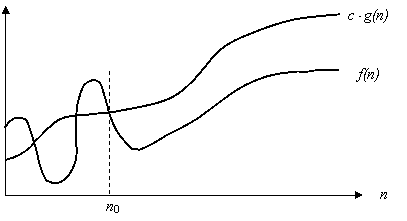
Fig.3.b. Reprezentarea lui f(n) = O(g(n))
In baza formulei 3.a], se poate demonstra faptul ca orice functie patratica a n + b n + c , a > este O(n 2).
o Pur si simplu se alege valoarea constantei c astfel incat sa fie mai mare decit a. Termenii de grad mai mic ca 2 se neglijeaza.
o Este surprinzator faptul ca functia liniara a n + b este de asemenea O(n 2), lucru usor de verificat in baza aceleasi formule 3.a], daca se alege c = a + | b | si n0 = 1.
Notatia O este de obicei cea mai utilizata in aprecierea timpului de executie al algoritmilor respectiv a performantei acestora.
Ea poate fi uneori apreciata direct din inspectarea structurii algoritmului, spre exemplu existenta unei bucle duble conduce imediat la o margine de ordinul O(n 2)
Deoarece notatia O descrie o margine superioara, cand este utilizata pentru a margini cazul cel mai defavorabil de executie al unui algoritm, prin implicatie ea margineste superior comportamentul algoritmului in aceeasi masura pentru orice intrare.
Cele mai obisnuite ordine de marime ale notatiei O se afla in relatiile de ordine prezentate in [3.c], iar reprezentarea lor grafica la scara logaritmica apare in fig.3.c.
O(1) < O(log n) < O(n) < O(n log n) < O(n ) < O(n ) <
< O(2n) < O(10 n) < O( n ! )
< O(n n) [3.c]
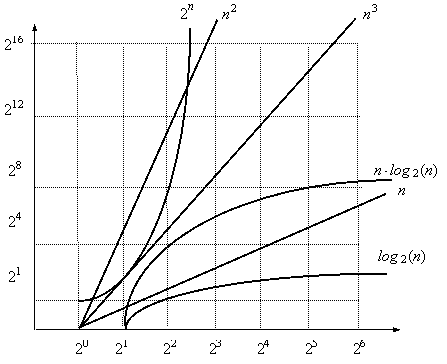
Fig. 3.c. Ordine de marime ale notatiei O
In acelasi context in [3.d] se prezinta cateva sume intregi utile care sunt frecvent utilizate in calculul complexitatii algoritmilor.
![]()
![]()
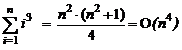 [3.d]
[3.d]
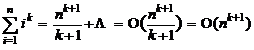
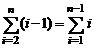
Demonstratie:
f(n) = O(g(n)) T c , n f(n) c1 g(n) pentru n > n
g(n) = O(h(n)) T c , n g(n) c2 h(n) pentru n > n
f(n) c ( c h(n))
Exemplul 3. Se considera expresia
8 n log(n) + 4 n
si se cere o estimare a sa in termenii notatiei O.
Se procedeaza dupa cum urmeaza:
o log (n) = O(n1/ 2) deoarece logaritmul unui numar este mai mic decat orice putere pozitiva a numarului in baza urmatoarei teoreme:
o Fie a > 0 si a
o Pentru exponent d > 0 exista un numar N astfel incat pentru x > N avem log a x < x d
o n log(n) = O(n n O(n 3/2) (Regula 5).
o n log(n) = O(n 3/2) (Regula 2).
o n = O(n 3/2) (Regula 2).
o n log(n) + n = O(max ) =
O(max O(n 3/2) (Regula 4).
Cu ajutorul notatiei O mare se poate aprecia timpul de executie al unui algoritm.
Se face sublinierea ca se poate aprecia timpul de executie al unui algoritm abstract si nu al unui program intrucat acesta din urma depinde de mai multi factori:
o (1) Dimensiunea si natura datelor de intrare
o (2) Caracteristicile sistemului de calcul pe care se ruleaza programul
o (3) Eficienta codului produs de compilator.
Notatia O mare permite eliminarea factorilor care nu pot fi controlati (spre exemplu viteza sistemului de calcul) concentrandu-se asupra comportarii algoritmului independent de program.
o In general un algoritm a carui complexitate temporala este O(n 2) va rula ca si program in O(n 2) unitati de timp indiferent de limbajul sau sistemul de calcul utilizat.
In aprecierea timpului de executie se porneste de la ipoteza simplificatoare deja enuntata, ca fiecare instructie utilizeaza in medie aceeasi cantitate de timp.
Instructiunile care nu pot fi incadrate in aceasta medie de timp sunt:
o (1) Instructiunea IF
o (2) Secventele repetitive (buclele)
o (3) Apelurile de proceduri si functii.
Presupunand pentru moment ca apelurile de proceduri si functii se ignora, se adopta prin conventie urmatoarele simplificari:
o (1) Se presupune ca o instructiune IF va consuma intotdeauna timpul necesar executiei ramurii celei mai lungi, daca nu exista ratiuni contrare justificate;
o (2) Se presupune ca intotdeauna instructiunile din interiorul unei bucle se vor executa de numarul maxim de ori permis de conditia de control.
Exemplul 4.a.
Se considera o procedura care:
o (1) Cauta intr-un tablou a cu n elemente, un element egal cu cheie
o (2) Returneaza in variabila unde ultima locatie in care este gasita cheia sau zero in caz contrar [4.a].
PROCEDURE CautareLiniara(n,cheie: integer,
a: TablouNumeric; VAR unde: integer);
VAR indice: integer;
BEGIN
unde: = 0
FOR indice:= 1 TO n DO
IF a[indice]= cheie THEN [4.a]
unde:= indice
END
Intrarea in procedura si initializarea O(1)
variabilei unde
Bucla FOR (n reluari) O(1+n+1) = O(n)
Instructiunea IF si O(1) O(n*1) = O(n)
ramura sa
Revenirea din procedura O(1)
Fig. 4.a. Schema temporala a algoritmului [4.a]
In figura 4.a apare schema temporala a algoritmului impreuna cu estimarea O mare corespunzatoare.
In analiza au fost introduse si operatiile de intrare si revenire din procedura care nu apar ca parti explicite ale rutinei.
Pe viitor apelul si revenirea din procedura vor fi omise din analiza temporala deoarece ele contribuie cu un timp constant la executie si nu influenteaza estimarea O mare
Exemplul 4.b Se considera urmatoarea portiune de cod [4.b].
FUNCTION SumProd(n: integer): integer;
VAR rezultat,k,i: integer;
BEGIN
rezultat:= 0;
FOR k:= 1 TO n [4.b]
FOR i:= 1 TO k
rezultat:= rezultat+k*i;
SumProd:= rezultat
END;

initializare rezultat O(1)

 bucla FOR (n
reluari)
bucla FOR (n
reluari)
bucla FOR (n reluari)
O(n*1) = O(n) O(n*n) = O(n2) O(1+n2) = O(n2)
![]() interior O(1)
interior O(1)
Fig. 4.b. Schema temporala a algoritmului din secventa [4.b]
La analiza complexitatii temporale se face presupunerea ca ambele bucle se reiau de numarul maxim de ori posibil
o In realitate acest lucru nu este adevarat deoarece bucla interioara se executa cu limita k n ( si nu cu limita n)
Se va demonstra ca prin aceasta simplificare estimarea temporala finala nu este afectata.
La o analiza mai aprofundata se tine cont de faptul ca bucla FOR interioara se executa prima oara o data, a doua oara de 2 ori s.a.m.d, a k-oara de k ori.
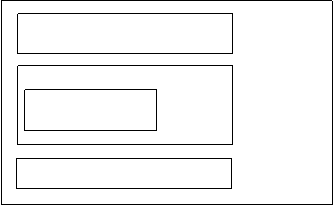
o In consecinta numarul exact de reluari este cel precizat de expresia de mai jos si dupa cum se observa el este O(n2)
![]()
1 + 2 + 3 + + n = [4.c]
In mod analog in cadrul secventei [4.d] se ajunge la estimarea: O(n n n) = O(n3).
FOR i:= 1 TO n DO
FOR j:= 1 TO i DO
FOR k:= 1 TO i DO [4.d]
Secventa ;
12 + 22
+ 32 + + n 2
= ![]() = O(n 3) [4.e]
= O(n 3) [4.e]
Presupunem ca un algoritm a fost conceput, implementat, testat si depanat pe un sistem de calcul tinta
Ne intereseaza profilul performantei sale, adica timpii precisi de executie ai algoritmului pentru diferite seturi de date, eventual pe diferite sisteme tinta.
o Pentru aceasta sistemul de calcul tinta trebuie sa fie dotat cu un ceas intern si cu functii sistem de acces la acest ceas.
Dupa cum s-a mai precizat, determinarea profilului performantei face parte din testul ulterior al unui algoritm si are drept scop determinarea precisa a ordinul de marime al timpului de executie al algoritmului.
o Informatiile rezultate sunt utilizate de regula pentru a valida sau invalida, respectiv pentru a nuanta rezultatele estimarii apriorice.
Se presupune un algoritm implementat in forma unui program numit Algoritm(X: Intrare,Y: Iesire)unde X este intrarea iar Y iesirea.
Pentru a construi profilul algoritmului este necesar sa fie concepute:
o Seturile de date de intrare a caror dimensiune creste intre anumite limite, pentru a studia comportamentul algoritmului in raport cu dimensiunea intrarii
o Seturile de date care in principiu se refera la cazurile extreme de comportament.
o O procedura cu ajutorul careia poate fi construit profilul algoritmului in baza seturilor de date anterior amintite.
procedure Profil;
begin
*initializeaza procedura Algoritm;
*afiseaza('Testul lui Algoritm. Timpii in milisecunde');
repeat
*citeste(SetDeDate); [5.a]
*afiseaza('Un nou set de date:', SetDeDate);
*apel TIME(t);
*apel Algoritm(SetDeDate, Rezultate);
*apel TIME(t1);
*afiseaza('TimpExecutie=', t - t1);
until sfarsit(SetDeDate)
end
Procedura Profil poate fi utilizata in mai multe scopuri functie de obiectivele urmarite.
o Evidentierea performantei intrinseci a unui algoritm precizat.
Pentru aceasta se aleg, asa cum s-a mai precizat, seturi de date cu dimensiuni din ce in ce mai mari.
Rezultatul va fi profilul algoritmului.
Pentru deplina conturare a profilului se testeaza de asemenea si cazurile de comportament extrem ale algoritmului respectiv cazul cel mai favorabil respectiv cazul cel mai defavorabil.
o (2) Evidentierea performantei relative a doi sau mai multi algoritmi diferiti care indeplinesc aceeasi sarcina.
In acest scop se executa procedura Profil pentru fiecare din algoritmi in parte, cu aceleasi seturi de date intiale, pe un acelasi sistem de calcul.
Compararea profilelor rezultate permite ierarhizarea performantelor algoritmilor analizati.
Trebuie insa acordata o atentie speciala procedurii TIME a caror rezultate in anumite circumstante pot fi nerevelevante.
o Astfel, in cazul sistemelor time-sharing, al sistemelor complexe care lucreaza cu intreruperi sau al sistemelor multi-procesor, timpul furnizat de aceasta functie poate fi complet needificator.
o In astfel de cazuri, una din solutii este aceea de a executa programul de un numar suficient de ori si de a apela la metode statistice pentru evidentierea performantelor algoritmului testat.
6. Rezumat
Prin algoritm se intelege o modalitate de rezolvare a unei probleme utilizand un sistem de calcul. Un algoritm este de fapt o metoda sau o reteta pentru a obtine un rezultat dorit.
Din punct de vedere formal in definirea unui algoritm se porneste de la un set de date initiale care abstractizeaza contextul problemei de rezolvat, asupra caruia se aplica un set de relatii de transformare
Un algoritm se bucura de urmatoarele proprietati: generalitate, finitudine si unicitate
Analiza unui algoritm se desfasoara in doua etape: (1) analiza apriorica care are drept scop principal determinarea teoretica a ordinului de marime al timpului de executie al unui algoritm si (2) testul posterior are ca scop principal stabilirea profilului algoritmului.
Pentru aprecierea ordinului de marime al timpului de executie al unui algoritm se utilizeaza notatiile asimptotice
Notatia O este o notatie asimptotica care desemneaza marginea asimptotica superioara a unei functii. Notatia O este utilizata in aprecierea timpului de executie al algoritmilor. Ea poate fi uneori apreciata din inspectarea structurii algoritmului. Pentru a simplifica aceasta activitate se utilizeaza regulile aritmeticii ordinale a notatiei O
Aprecierea timpului executie al unui algoritm se realizeaza de regula analizand schema sa temporala in termenii notatiei O.
Profilarea unui algoritm se realizeaza pe baza masurarii timpilor de executiei ai algoritmului pentru diverese seturi de date.
7. Exercitii
Definiti notiunea de algoritm. Care sunt elementele constitutive ale unui algoritm?
Care sunt proprietatile de care se bucura un algoritm?
La ce serveste analiza algoritmilor? Care sunt etapele analizei unui algoritm?
Cum se defineste notatia O?
Care este relatia de ordonare a celor mai obisnuite ordine de marime al e notatiei O?
Care sunt regulile aritmeticii ordinale a notatiei O?
Se cere sa se estimeze in termenii functiei O urmatoarea expresie: 3n2+5n+25n*log(n)
Se cere sa se estimeze in termenii notatiei O timpul de executie al algoritmuli de cautare liniara respectiv al algoritmului de cautare binara.
Ce este profilarea unui algoritm? Schitati o functie cu ajutorul careia se poate construi profilul unui algoritm oarecare. Care sunt etapele constructiei profilului unui algoritm?
Copyright © 2025 - Toate drepturile rezervate