 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Sectiune parabolica in conuri
Parabola, (fig.3.51), este o conica cu ecuatia:y2=2px, daca se ia axa parabolei, axa Ox, varful parabolei originea O, a sistemului Oxy si tangenta in acest punct, axa Oy. Parabola este o conica cu o singura axa de simetrie, nu are diametrii conjugati, nu are centru. Ecuatia directoarei este x=-(p/2)
![]()

sectiune plana de tip parabola, se determina conform teoremei lui Dandelin. Elementele sectiunii se determina din proprietatile analitice ale conului, ale planului de sectiune si ale parabolei de intersecte, prin metodele geometriei descriptive. punctele de intersectie se determina prin metodele geometriei descriptive.
con circular, drept, plan de capat, [P], (fig.3.52).
Determinarea naturii sectiuni. Se
duce prin varful conului un plan [Q], de urme Q, Q', paralel, cu planul dat. urma verticala a planului, Q', se suprapune peste
proiectia verticala a generatoarelor SA(sa, s'a'), SA1(sa1,
s'a1'). urma
orizontala a planului, Q,
este tangenta la baza conului in proiectia a. planul [Q], este un plan tangent
conului. planul de
capat, [P], paralel cu planul [Q], determina o sectiune
plana de tip parabola, conform teoremei lui
Dandelin Determinarea
sectiunii. planul de capat,
[P], intersecteaza baza conului in punctele 1(1,1'),
Sectiune plana, rezultata din intersectia unui
plan de capat, [P], de urme P, P', cu un con drept, circular, cu CO(o,o'),
baza, un cerc, in planul orizontal de proiectie si cu V(v,v') varful
se determina prin:
Fig.3.52
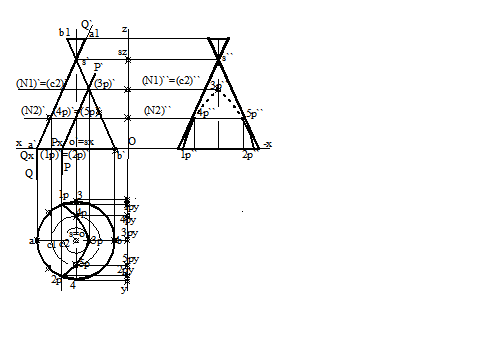
2(2,2'), puncte reale de intersectie. Proiectia orizontala, 1 si 2, se determina direct. se ridica in proiectie verticala si se determina proiectia verticala, 1' si 2' a punctelor de intersectie. Punctul 3p(3p, 3p'), de intersectie a urmei verticale, P', cu generatoarea SB(sb, s'b') a conului este varful sectiunii. Alte puncte de intersectie, 4p(4p,4p') si 5p(5p, 5p'), sunt determinate prin intersectia conului si a planului dat cu planele de nivel, [n1], respectiv [n2]. Pentru punctele 4p(4p,4p') si 5p(5p, 5p'), intersectia cu conul este cercul c2(c2, c2'). Intersectia cu planul este dreapta de capat, d2(d2, d2`). Intersectia dintre cercul c2(c2, c2') si dreapta d2(d2,d2) sunt punctele, 4p(4p,4p') si 5p(5p, 5p'). Parabola de sectiune este 5p5p5p5p5p p2p3p4p5p p'2p'3p'4p'5p', p'`2p'`3p'`4p'`5p'`), proiectia verticala p'2p'3p'4p'5p', fiind pe urma verticala, P', a planului de sectiune, [P]. proiectia laterala, p'`2p'`3p'`4p'`5p'`, se obtine din cele doua proiectii determinate.
Vizibilitatea
Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor. In proiectie orizontala este vizibila intreaga curba, fiind pe suprafata laterala a conului drept, daca nu se ia in considerare cea de a doua panza a conului. In proiectielaterala, curba este vizibila de la abscise mai mari decat cele ale proiectiilor 3, 4, respectiv de la intersectia cu segmentul 34.
con circular, drept, plan oarecare, [P], (fig.2.53), (fig.2.54).
Sectiune plana, rezultata din intersectia unui plan oarecare, [P], de urme P, P', cu un con drept, circular, cu CO(o,o'), baza,
un cerc, in planul orizontal de proiectie
si cu s(s, s') varful se
determina prin: Determinarea
naturii sectiuni. Se duce un plan oarecare, [P], de urme
P, P', paralel cu un plan tangent, [t],
de urme t, t'. Determinarea sectiunii. Punctele de intersectie dintre
urma orizontala, P,
a planului dat si baza conului, determina proiectia
orizontala, 1p si 2p, a punctelor reale de
intersectie, 1p(1p,1p'),
2p(2p,
2p').
Fig.3.53
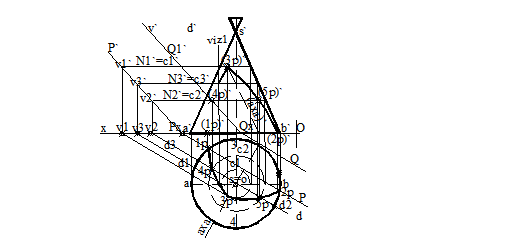
Fig.3.54 se ridica in proiectie verticala si
se determina proiectia
verticala, 1p' si 2p' a punctelor de
intersectie. Punctul 3p(3p, 3p'),de intersectie a liniei de cea
mai mare panta a planului [P], care este proiectia
orizontala, a axei parebolei, notata cu AXA(axa, axa'), din centrul bazei O(o,o'), cu
conul, este varful sectiunii. Este determinat prin metoda de
determinare a intersectiei dintre o dreapta si un con. Alte
puncte de intersectie, 4p(4p,4p')
si 5p(5p,
5p') sunt determinate prin intersectia conului si a
planului dat cu planul de nivel, [n2].
Pentru punctele 4p(4p,4p')
si5p(5p,
5p'),
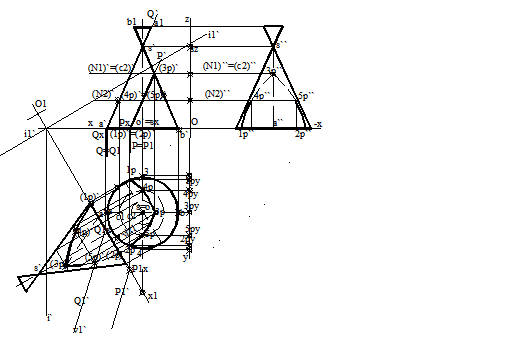
intersectia cu conul este cercul c2(c2, c2'). Intersectia cu planul secant, este dreapta d2(d2, d2). Intersectia dintre cercul c2(c2, c2') si dreapta d2(d2, d2`) sunt punctele, 4p(4p,4p') si 5p(5p, 5p'). La fel se pot determina si alte puncte de intersectie.
Vizibilitatea
Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor. In proiectie orizontala este
vizibila intreaga curba, fiind pe suprafata laterala a conului drept. In proiectie
verticala, curba este vizibila de la departari mai mari decat departarea proiectiilor a, b, respectiv de la intersectia cu segmentul ab. Se determina in proiectia verticala urma (n3)`, a planul de nivel, [n3], corespunzator proiectiei orizontale c3, a cercului determinat de intersectia cu segmentul ab. intersectia cu segmentul ab, se ridica in proiectia verticala pe urma (n3)`. Linia de ordine din planul orizontal de proiectie, care determina punctul de schimbare a vizibilitatii in planul vertical de proiectie este notata cu viz1.
Pentru con circular, oarecare, determinarea elementelor parabolei are urmatoarele caracteristici: axa parabolei este paralela cu generatoarea de tangenta, varful parabolei este punctul in care tangenta la sectiune, este perpendiculara pe generatoarea de intersectie, sau paralela cu dreapta de intersectie dintre planul [T si planul perpendicular pe generatoarea de intersectie, dus prin varful conului.
con circular, oarecare, plan de capat, [P], (fig.2.55).
Sectiune plana, rezultata din intersectia unui plan oarecare, [P], de urme P, P', cu un con drept, circular, cu CO(o,o'), baza, un cerc, in planul orizontal de proiectie si cu s(s, s') varful se determina prin:
Determinarea naturii sectiuni.
Se duce un plan de urme t, t', paralel cu planul oarecare, [P], dat, de urme P, P'. planul, [t], este tangent conului dat, de-a lungul generatoarei S2(s2, s`2`, s``2``). Sectiune plana, rezultata din intersectia planului [P] cu planul [t], este o parabola.
Determinarea sectiunii.
in proiectie verticala sectiunea plana este pe urma verticala P
Punctele de intersectie dintre urma orizontala, P, a planului dat si baza conului, determina proiectia orizontala, 1p si 2p, a punctelor reale de intersectie, 2p(2p, 2p'), 3p(3p, 3p'). se ridica in proiectie verticala si se determina proiectia verticala, 2p' si 3p' a punctelor de intersectie. Alte puncte ale sectiunii se determina prin plane auxiliare, de nivel, de front, etc.
Varful parabolei, este punctul in care tangenta la parabola este perpendiculara pe axa parabolei sau paralela cu dreapta de intersectie, d(d, d'), dintre planul [t] si planul [P1]. planul, [P1] este planul perpendicular pe generatoarea S2(s2, s`2`, s``2``), dus prin varful S(s, s`, s``). Prin dreapta de intersectie d(d, d'), se duce planul tangent [t1], de urme t1, t1'. planul tangent [t1], este de-a lungul generatoarei S7(s7, s`7`, s``7``), pe care este situat varful 1p(1p,1p'). Intersectia dintr dreapta d(d, d') si planul de sectiune [P] este varful parabolei de sectiune, 1p(1p,1p').
Axa, este paralela cu generatoarea de tangenta S2(s2, s`2`, s``2``). Prin varful
parabolei de sectiune, 1p(1p,1p') se construieste paralela la generatoarea S2(s2, s`2`, s``2``) si se noteaza cu Axa(axa, axa')
Vizibilitatea
Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor. In proiectie orizontala este vizibila intreaga curba, fiind pe suprafata laterala, vizibila, a conului. In proiectie verticala, curba este vizibila si este pe urma P', a planului, pentru departari mari decat departarea proiectiilor a, b, respectiv de la intersectia cu segmentul ab, din proiectia verticala. In proiectie laterala, curba este vizibila fiind pe suprafata laterala, vizibila, a conului, respectiv, fiind de la abscise mai mari decat cele ale proiectiilor 5, 6, respectiv de la intersectia cu proiectia 56.
adevarata marime a sectiunii, se determina prin rabatere pe plan orizontal de proiectie, axa de rabatere fiind urma P
con circular, oarecare, plan oarecare, [P], (fig.3.56), (fig.3.57).
Fig.3.56 Fig.3. 55
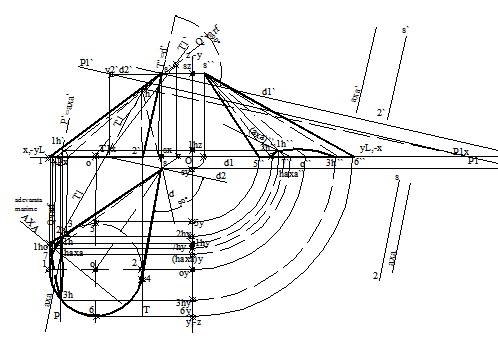
Sectiune plana, rezultata din intersectia unui plan oarecare, [P], de urme P, P', cu un con drept, circular, cu CO(o,o'), baza, un cerc, in planul
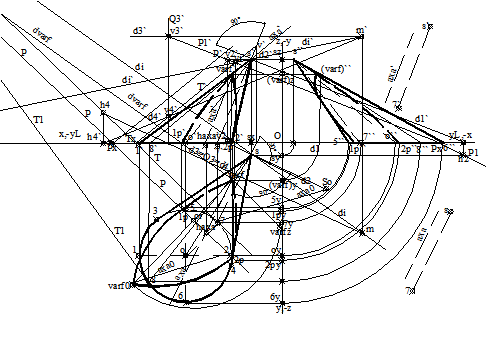
planul, [t], este tangent conului dat, de-a lungul generatoarei
S7(s7, s`7`, s``7``). Sectiune plana, rezultata din intersectia Fig.3.57 orizontal de proiectie si cu s(s, s') varful se determina
prin: Determinarea naturii sectiuni. Se duce un plan [t], de urme t, t',
paralel cu planul oarecare, [P], dat, de urme P, P'.
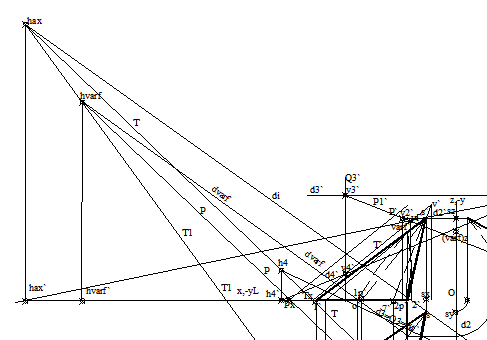
planului [P] cu planul [t], este o parabola.
Determinarea sectiunii.
Punctele de intersectie dintre urma orizontala, P, a planului dat si baza conului, determina proiectia orizontala, 1p si 2p, a punctelor reale de intersectie, 1p(1p,1p'), 2p(2p, 2p'). se ridica in proiectie verticala si se determina proiectia verticala, 1p' si 2p', a punctelor de intersectie. Alte puncte ale sectiunii se determina prin plane auxiliare, de nivel, de front, etc.
Varful parabolei si axa, parabolei se determina ca si la intersectia anterioara. Se noteaza varful cu VARF(varf, varf`) si axa cu AXA(axa, axa`).
Vizibilitatea
Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor. In proiectie orizontala este invizibila intreaga curba, fiind pe suprafata laterala, invizibila, a conului. In proiectie verticala, intreaga curba este invizibila fiind pe suprafata laterala, invizibila, a conului. In proiectie laterala, curba este vizibila pentru portiunea cuprinsa intre proiectiile orizontale, 1p si 5, fiind pe suprafata laterala, vizibila in proiectie laterala, a conului, respectiv, fiind de la abscise mai mari decat cele ale proiectiilor 5, 6. Intre proiectiile 5 si 2p, curba este invizibila.
adevarata marime a sectiunii, se determina prin rabatere pe plan orizontal de proiectie, axa de rabatere fiind urma P
Alte puncte ale sectiunii, se determina din proprietatile parabolei sau prin determinarea intersectiilor planului de sectiune si a conului cu plane auxiliare, de nivel, de front, etc.
3.1.3. Sfera
Sectiunile plane prin sfera sunt cercuri, indiferent de pozitia planului de sectiune.
sectiunea plana cu un plan paralel cu planul vertical de proiectie este numit meridian, (fig.3.58a), (fig.3.58b), sectiunile plane prin sfera cu un plan paralel cu planul orizontal de proiectie numindu-se numite paraleli, acestea fiind planele auxiliare utilizate in determinarea. sectiunilor plane. planul paralel cu planul vertical de proiectie este [F], cu urma orizontala, F. sectiunea plana determinata prin sfera este un cerc cu centrul O1( o1, o1`). Proiectia verticala a cercului este un cerc, care are proiectia centrului in centrul sferei, o`=o1`. Proiectia orizontala a cercului este pe urma orizontala F, segmentul de dreapta 1f2f. planul paralel cu planul orizontal este[N], cu urma verticala, N` Proiectia
Fig.3.58 b. a. verticala a cercului este pe urma verticala, N` segmentul de dreapta 1n`2n`. Proiectia orizontala a cercului este un cerc cu
centrul O1( o1, o1`), in centrul sferei, o=o1, proiectia razei fiind 1no. sectiunea plana cu un plan de capat, [P],
de urme P, P` si P``
Intersectia cu plan de capat, (fig.3.59),
(fig.3.60)
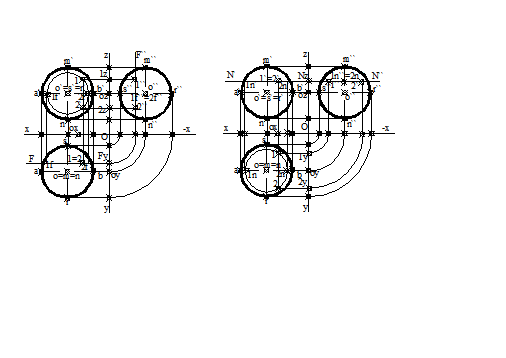
este un cerc cu centrul O1( o1, o1`) si raza, R=1`o1`, care este in adevarata marime in planul vertical de proiectie pe urma P`, a planului dat. Proiectia verticala a centrului cercului, o1`, este la mijlocul segmentului 1`2`, punctele de intersectie dintre P` si conturul aparent vertical al sferei. Proiectia verticala
Fig.3.59 a cercului este pe urma verticala, P`, segmentul de dreapta 1`2`.
vertical al sferei.
Proiectia orizonta la a cercului este o elipsa cu
centrul o1, proiectia orizontala a centrului cercului de
sectiune. Axa mare a elipsei este dreapta de capat, cu
proiectia 34, ce trece prin punctul O1( o1, o1`)
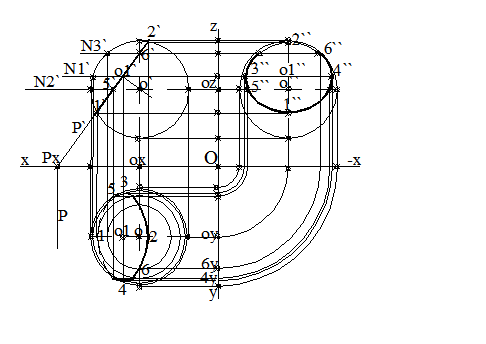
Fig.3.60 Axa mica, a
elipsei este orizontala, cu proiectia 12, ce trece prin punctul O1(
o1, o1`).
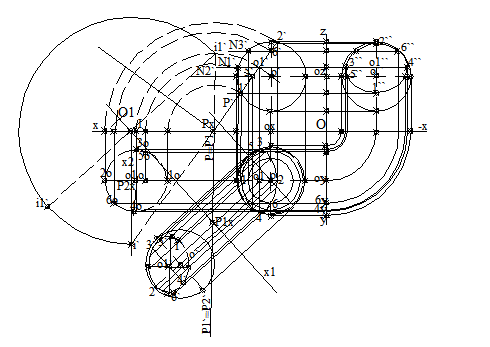
Proiectia laterala, a cercului este o elipsa cu centrul o1``, proiectia laterala a centrului cercului de sectiune. Axa mare a elipsei este proiectia, 3``4``, proiec-
Fig.3.61
tia laterala a dreaptei de capat ce trece prin punctul O1( o1, o1`, o1``). Axa mica, a elipsei este frontala, cu proiectia 1``2``, ce trece prin punctul O1( o1, o1`, o1``).
Vizibilitatea. Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor. In proiectie orizontala vizibilitatea este determinata planul de nivel [N2], care determina conturul aparent orizontal al sferei. intersectia cu plane de nivel cu cote mai mari decat cotele planului [N2], este vizibila, intersectia cu plane de nivel cu cote mai mici decat cotele planului [N2], este invizibila. Elipsa este invizibila intre punctele de proiectie orizontala, 5,1,6. intersectia dintre planul [P] si planul de nivel [N2], este dreapta de capat, cu punctele 5, 6, proiectia orizontala a intersectiei. intersectia dintre planul de nivel [N2] si sfera este paralelul de proiectie orizontala cercul c2. intersectia dintre dreapta de capat si paralelul, c2, sunt punctele de proiectie orizontala, 5,6 de pe conturul aparent orizontal al sferei. intre punctele de proiectie orizontala, 5,1,6, cotele sunt mai mici. Elipsa este vizibila intre punctele de proiectie orizontala, 5,2,6, cotele sunt mai mari. In proiectia laterala, elipsa este invizibila intre punctele de proiectie laterala, 7``, 2``, 8``. vizibilitatea stabilindu-se dupa abscise. Punctele cu abscise mai mari decat abscisa proiectiilor orizontale 3s, 4s, sunt vizibile. Punctele cu abscise mai micii decat abscisa proiectiilor orizontale 3s, 4s, sunt invizibile. pentru puncte vizibile.
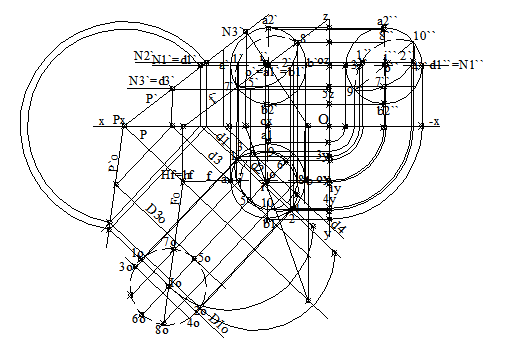
sectiunea plana cu un plan oarecare, [P], de urme P, P` si P`` este un cerc cu centrul I( i, i`), care este in cele trei proiectii o elipsa.. Intersectia dintre dreapta dusa prin centrul sferei, perpendiculara pe planul de sectiune si sfera este centrul cercului de sectiune, I( i, i`), respectiv centrul proiectiilor acestuia, elipsele din cele trei proiectii. Se rabate centrul I( i, i`), pe planul orizontal de proiectie. raza, R=1o2o, cercului de sectiune este in adevarata marime pe orizontala sau frontala, duse prin centrul sferei. Se determina punctele de intersectie, 1(1, 1`), 2(2, 2`), dintre planul [P] si sfera. Planul auxiliar pentru determinarea punctelor este planul orizontal, [N1], dus prin centrul sferei. intersectia dintre planul orizontal, si planul dat, este orizontala d(d, d`). intersectia dintre planul orizontal, si sfera, este conturul aparent orizontal al sferei. intersectia dintre orizontala si conturul aparent orizontal al sferei, sunt punctele de intersectie din proiectia orizontala 1 si 2. Segmentul 12, este raza cercului de sectiune in adevarata marime. Cu linii de ordine, se determina proiectiile verticale, 1`, 2`, pe urma verticala N1`. Se rabate pe planul orizontal de proiectie si se construieste cercul de sectiune. Se determina alte puncte de intersectie, prin intoarcere din rabatere. Se determina punctele de intersectie, 3(3, 3`), 4(4, 4`), de pe frontala F(f, f`). Se determina punctele de intersectie, 5(5, 5`), 6(6, 6`), care definesc proiectia cercului de sectiune, elipsele din cele trei proiectii. punctele de intersectie pot fi determinate si cu plane auxiliare. punctele de intersectie, 3(3, 3`), 4(4, 4`), dintre planul [P] si sfera se determina cu planul auxiliar de front, [F1], dus prin centrul sferei. intersectia dintre planul de front, si planul dat, este frontala F(f, f`). intersectia dintre planul de front, si sfera, este conturul aparent vertical al sferei. intersectia dintre frontala si conturul aparent vertical al sferei, sunt punctele de intersectie din proiectia verticala 3` si 4`. Cu linii de ordine, se determina proiectiile orizontale, 3, 4, pe urma orizontala F1.
Vizibilitatea.
Pentru determinarea vizibilitatii se aplica regulile de la vizibilitatea figurilor plane si de la reprezentarea corpurilor.
Elementele proiectiilor cercului de sectiune
Elementele elipselor din proiectiile orizontala si verticala, au pozitii particulare, sunt pe drepte orizontale, pe drepte frontale, sau pe liniile de cea mai mare panta, a planului de sectiune. In planul lateral de proiectie se determina cu regulile de determinare a celei de a treia proiectii.
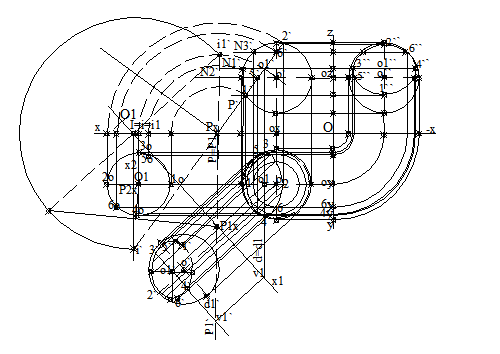
Se determina sectiunea plana cu un plan de capat [P], de urme P, P` si P``si cu schimbare de plan de proiectie vertical se determina si sectiunea plana cu un plan oarecare, [P1], de urme P1, P1` si P1``. Se utilizeaza metoda de rabatere pe
plan
orizontal de proiectie a cercului de sectiune si metoda
planelor auxiliare. Vizibilitatea, se stabileste cu aceleasi reguli. Fig.3.62
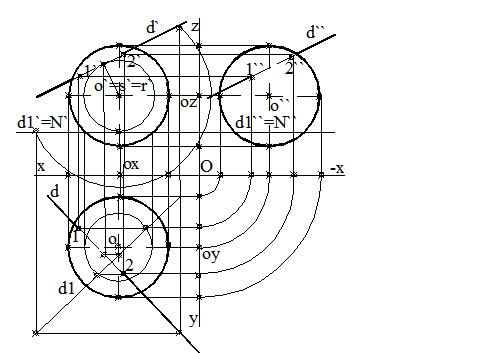
ale dreptei cu cercul de
intersectie.Punctele astfel obtinute se intorc pe dreapta in
pozitia initiala. Punctele de intersectie sunt 1(1, 1`)
si 2(2, 2`). [N1]. Se
determina punctele de intersectie Fig.3.63 lor plane, (fig.3.62)
ei sfera-dreapta. Se rote
ste dreapta data d(d, d`) in pozitie de
dreapta orizontala si se determi
na intersectia dintre sfe
ra si planul de nivel,
Aplicatie a sectiuni
sectiunile plane se utilizeaza la deter-
minarea intersecti-
Copyright © 2025 - Toate drepturile rezervate