Pendul elastic

Scopul lucrarii

Experimentul prezentat are ca scop determinarea constantei de elasticitate a unui oscilator, mai precis, al pendulului elastic. Vom intreprinde acest lucru prin verificarea relatiilor intre perioada pendulului elastic si masa, respectiv constanta de elasticitate. Vom parcurge acest lucru si prin estimarea modulului de elasticitate al cauciucului.

Elemente de teorie

Numim pendul elastic un sistem alcatuit dintr−un corp relativ dens, atasat de un corp aproape perfect elastic si avand masa neglijabila.

Legea perioadei pendulului elastic este:

m = masa corpului prins de resort ;

k = constanta de elasticitate a resortului.

In experimentul de fata, am utilizat mai multe benzi elastice, realizand astfel un sistem de resorturi grupate in serie, cu o constanta K=k/n, unde "k" este constanta de elasticitate corespunzatoare unitatii,iar "n" numarul de elemente din serie.

Din acest motiv, relatia definita anterior devine .

Dupa cum vom mentiona ulterior, a fost necesar sa recurgem la oscilatii intretinute,intrucat majoritatea oscilatoarelor au pierderi energetice, mai mici sau mai mari, in functie de calitatea materialelor folosite si de mediul de utilizare.Aceste pierderi conduc la ceea ce se numeste amortizare, adica atenuarea miscarilor de oscilatie, intr-o anumita perioada de timp.

Teoretic, oscilatiile unui punct (sistem) material inceteaza dupa o perioada aproape infinita de timp, insa in practica aceasta perioada este foarte scurta, deoarece daca amplitudinea scade sub o anumita valoare, miscarea intregului ansamblu devine imposibila.

Energia transmisa unui sistem oscilant,in cazul amortizarilor, este cheltuita ca lucru mecanic necesar invingerii fortlor rezistente amintite anterior, fiin astfel necesara alimentarea cu energie din exterior.Daca sursa energiei face parte din sistem, atunci acesta se numeste autooscilant (ex.: ceasornicul cu pendul).

Metoda

In continuare, vom prezenta masa (m) si numarul de resorturi (n) ca functii liniare de ,dupa cum urmeaza:

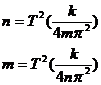
Folosind cele doua relatii, vom determina, intr-un punct al studiului de fata, o valoare necunoscuta "x" a masei.

Materiale si mod de lucru

Ca mod de lucru, am realizat 12 masuratori, in cadrul carora am alternat atat lungimea resortului-serie( intre 6 si 11 unitati), cat si masa (50 - 120 si o masa "x"), intretinand oscilatiile prin miscari repetate ale mainii de care era agatat resortul.

Motivul pentru care am apelat la oscilatiile intretinute a fost forta de frecare prea mare, si deci o amortizare prea rapida, care ar fi dus la o abordare ineficienta si laborioasa a masuratorii.

Materialele folosite au fost:

benzi elastice de aceleasi dimensiuni;

corpuri rigide de mase variabile;

cronometru;

Rezultate experimentale

Prelucrarea datelor si rezultate

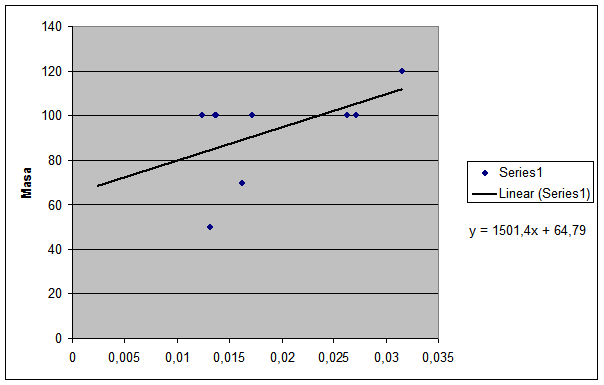
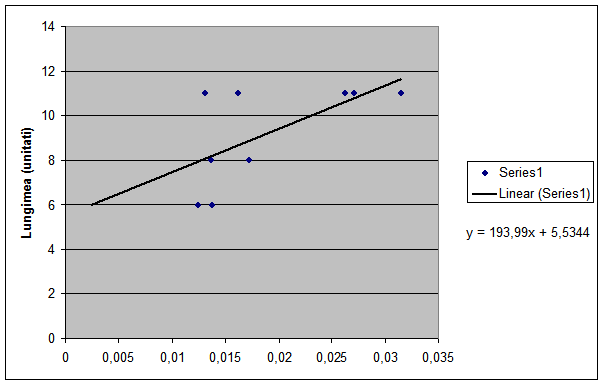
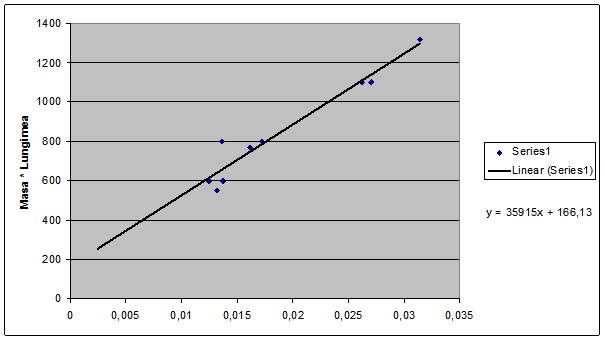
Din ultimul grafic se poate deduce "k", intrucat, conform si formulei deduse din ecuatia , ,deci x/y in cazul nostru. Astfel, valorile lui "k" variaza intre 5.8 si 4.2, deci media este 5.

In ceea ce priveste masa, cele 3 necunoscute au o valoare comuna, anume 90 g , explicandu-se astfel si apropierea ca marime de raportul ,asociat maselor de 100 g (0.026-0.028 fata de 0.025).

Comentarii

Ca in orice activitate umana, si in masuratorile efectuate in cadrul acestui experiment au intervenit erori; dintre ele, amintim:

Erori sistematice (vor fi intr-un singur sens datorita etalonarilor gresite);

Erori de metoda;

Imprecizia aparatelor de masurat;

Aproximarea masuratorilor si a valorilor numerice obtinute;

Erori umane.

Apreciand ca valoarea "5" este destul de mare, experimentul confirma datele reale, si anume ca, fara a intretine oscilatiile, amortizarea s-ar fi produs foarte rapid, in defavoarea obtinerii unor date concludente.

Bibliografie:

"FIZICA, Manual pentru clasa a IX-a",Anatolie Hristev, Vasile Falie, Editura Didactica si Pedagogica Bucuresti, 24.VII.1979;

Wikipedia.org;

"Manual de fizica clasa a XI-a", Rodica Ionescu, Cristina Onea, Ion Toma, editura Art, Bucuresti, 2007.

Proiectul a fost realizat de:

Grigore Adrian (obtinerea datelor experimentale si prelucrarea acestora);

Negroiu Diana (dactilografiere);

Tutu Mihai - Alexandru (obtinerea datelor experimentale si prelucrarea acestora).