 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Masurarea indicelui de refractie al unui esantion lamelar subtire cu fete plan - paralele. Metoda Chaulnes.
1.1. Exprimarea indicelui de refractie.
Direct sau prin simpla adaptare a relatiei punctelor conjugate pentru dioptrul sferic,
![]() (1.)
(1.)
la particularitatile sistemelor optice, se obtin relatii care permit descrierea proprietatilor de baza ale unei clase largi de esantioane optice.
De exemplu, folosind legile
reflexiei, putem initial stabili usor ca oglinda plana este
un sistem optic stigmatic, (asociind unui obiect punctual o singura
imagine punctuala), si ca imaginea ![]() a unui obiect real
punctual este virtuala si situata simetric cu obiectul
fata de planul oglinzii (fig. 1.)
a unui obiect real
punctual este virtuala si situata simetric cu obiectul
fata de planul oglinzii (fig. 1.)
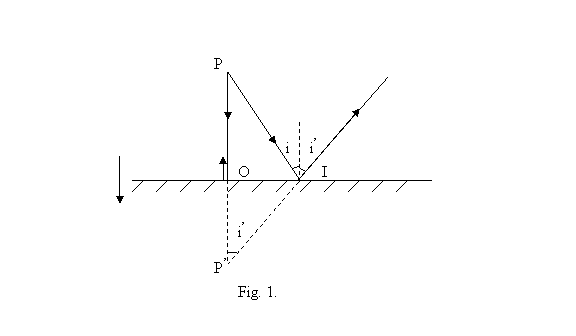
Din P pleaca razele incidente
PO si PI. Prelungirea razelor reflectate IR si OP determina,
prin intersectie imaginea ![]() .
.
Din egalitatea ![]() rezulta ca
cele doua triunghiuri dreptunghice cu latura OI comuna au unghiurile din
rezulta ca
cele doua triunghiuri dreptunghice cu latura OI comuna au unghiurile din ![]() si
si ![]() egale doua cate
doua si deci sunt congruente. In consecinta avem si
egalitatea:
egale doua cate
doua si deci sunt congruente. In consecinta avem si
egalitatea:
![]() , adica
, adica ![]() (2.)
(2.)
Daca
tratam oglinda plana ca un dioptru plan ![]() fictiv, atunci ecuatia dioptrului plan
rezultata din ecuatia (1.)
fictiv, atunci ecuatia dioptrului plan
rezultata din ecuatia (1.)
![]() (3.)
(3.)
devine compatibila cu rezultatul (2.) obtinut direct folosind legile reflexiei daca si numai daca
![]() (4.)
(4.)
In
consecinta, oglinda plana este un dioptru plan cu indicii de
refractie ![]() iar prima formula
fundamentala a unei oglinzi sferice capata forma :
iar prima formula
fundamentala a unei oglinzi sferice capata forma :
![]() (5.)
(5.)
care
permite (impreuna cu formulele a doua si a treia adaptate prin
relatia ![]() ) descrierea proprietatilor de optica
geometrica ale acestor oglinzi.
) descrierea proprietatilor de optica
geometrica ale acestor oglinzi.
Daca in prima formula
fundamentala a dioptrului sferic (1.) ne restrangem la limita ![]() ,
, ![]() ,atunci obtinem
prima formula a dioptrului plan, sub forma :
,atunci obtinem
prima formula a dioptrului plan, sub forma :
![]() (6.)
(6.)
Un obiect punctual real situat in pozitia ![]() in primul mediu are (in aproximatia gaussiana, deci
in limita incidentelor quasinormale) o imagine punctuala
virtuala ( fig. I2.a.) situata tot in primul mediu la distanta
in primul mediu are (in aproximatia gaussiana, deci
in limita incidentelor quasinormale) o imagine punctuala
virtuala ( fig. I2.a.) situata tot in primul mediu la distanta ![]() (7.)
(7.)
Similar, daca obiectul real
este in mediul (2) in pozitia ![]() , atunci imaginea virtuala are pozitia
, atunci imaginea virtuala are pozitia ![]() , situata la distanta ( fig.I2.b.)
, situata la distanta ( fig.I2.b.)
![]() (8.)
(8.)
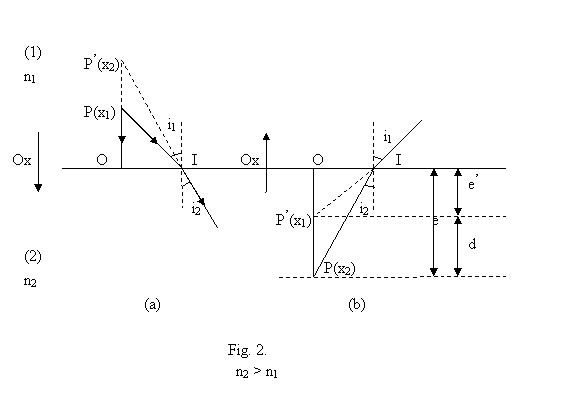
Alegem cazul (2.b.) al obiectului situat in mediul mai refringent. In acest caz imaginea se apropie de suprafata dioptrului.
Constructia imaginii
ramane aceeasi daca mediul (2) este restrans la o lamela cu
fete plan paralela si daca P este situat in mediul (2) sau,
la limita, pe granita plana (punctata) inferioara,
paralela cu planul superior al dioptrului, deoarece raza refractata ![]() nu traverseaza
granita plana inferioara a lamelei. In acest caz
nu traverseaza
granita plana inferioara a lamelei. In acest caz ![]() reprezinta
grosimea reala a lamelei,
reprezinta
grosimea reala a lamelei, ![]() deplasarea de apropiere a fetei inferioare de cea
superioara, iar
deplasarea de apropiere a fetei inferioare de cea
superioara, iar ![]() grosimea aparenta a lamelei.
grosimea aparenta a lamelei.
In acest fel, relatia (7.) indusa de formulele dioptrului plan, cazul (2.a), devine: .
![]() (9.)
(9.)
unde ![]() este noua notatie
pentru indicele de refractie al lamelei fata de mediul (1) (de
regula atmosfera cu
este noua notatie
pentru indicele de refractie al lamelei fata de mediul (1) (de
regula atmosfera cu ![]() , pentru care
, pentru care ![]() ).
).
Ultima relatie permite determinarea indicelui de refractie al lamelei (fata de mediul (1)) pe baza masurarii grosimi reale, e, si a deplasarii de apropiere, d, (marimi accesibile direct, mai simplu, in masurarile efectuate cu microscopul):
![]() (10.)
(10.)
(Alternativ, se pot masura grosimile reala si aparenta, e si e')
1.2 Determinarea directa pe baza legilor refractiei, a relatiei dintre indicele de refractie si grosimile reala si aparenta ale lamelei. (Tema de aprofundare).
In cazul fig. 2.b, in aproximatia
incidentei normale ![]() din
din ![]() si
si ![]() deducem succesiv :
deducem succesiv :
![]() ,
, ![]() (11.)
(11.)
![]()
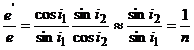 (12.)
(12.)
1.3. Metoda Chaulnes
Se aseaza pe
masuta microscopului lama de sticla suport ![]() care are pe
suprafata superioara, trasate repere din fabricatie sau cu
cerneala, de forma unor linii paralele. Se pune la punct grosier imaginea
unei linii rotind surubul cu cremaliera. Cu ajutorul surubului
micrometric de reglaj fin se pune la punct imaginea clara a aceleiasi
linii. Se noteaza indicatia
care are pe
suprafata superioara, trasate repere din fabricatie sau cu
cerneala, de forma unor linii paralele. Se pune la punct grosier imaginea
unei linii rotind surubul cu cremaliera. Cu ajutorul surubului
micrometric de reglaj fin se pune la punct imaginea clara a aceleiasi
linii. Se noteaza indicatia ![]() a surubului micrometric pentru aceasta
pozitie. Pe lama suport
a surubului micrometric pentru aceasta
pozitie. Pe lama suport ![]() se plaseaza lama
de studiat
se plaseaza lama
de studiat ![]() (cu indicele de
refractie si caracteristicile geometrice necunoscute), constatndu-se
ca imaginea liniei se altereaza. Se obtine din nou o imagine
clara a liniei rotind in continuare surubul micrometric. Se
noteaza indicatia
(cu indicele de
refractie si caracteristicile geometrice necunoscute), constatndu-se
ca imaginea liniei se altereaza. Se obtine din nou o imagine
clara a liniei rotind in continuare surubul micrometric. Se
noteaza indicatia ![]() a surubului
micrometric pentru pozitia in care se vede din nou clar vechea linie.
Notam cu y deplasarea implicata de rotatia surubului micrometric
cu o diviziune (
a surubului
micrometric pentru pozitia in care se vede din nou clar vechea linie.
Notam cu y deplasarea implicata de rotatia surubului micrometric
cu o diviziune (![]() mm pentru microscopul utilizat in laborator). Este evident ca
diferenta dintre a doua si prima citire este chiar deplasarea de
apropiere a liniei vizate initial, cauzata de asezarea lamelei
mm pentru microscopul utilizat in laborator). Este evident ca
diferenta dintre a doua si prima citire este chiar deplasarea de
apropiere a liniei vizate initial, cauzata de asezarea lamelei ![]() :
:
![]() (13.)
(13.)
Rotim acum surubul micrometric
in continuare pana la diviziunea ![]() , la care se observa clar imaginea unei noi linii special
trasate pe fata superioara a lamelei
, la care se observa clar imaginea unei noi linii special
trasate pe fata superioara a lamelei![]() . Grosimea reala este data de diferenta
dintre a treia si prima citire:
. Grosimea reala este data de diferenta
dintre a treia si prima citire:
![]() (14.)
(14.)
Pentru indicele de refractie, valoarea indusa de cele trei citiri
![]() este:
este:
![]() (15.)
(15.)
Masurarile
se reiau de 10 ori (![]() ,
, ![]() ). Se calculeaza mediile
). Se calculeaza mediile ![]() , erorile statistice absolute:
, erorile statistice absolute:
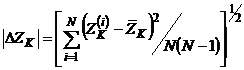 ;
; ![]() (16.)
(16.)
Exprimarea erorii relative pentru n,
![]() (17.)
(17.)
si evaluam valorile relative absolute
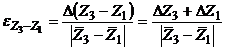 (18.)
(18.)
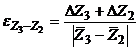 (19.)
(19.)
In
final se calculeaza ![]() si eroarea
absoluta
si eroarea
absoluta
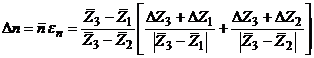 (20.)
(20.)
Datele se sintetizeaza in coloanele:
![]()
Copyright © 2025 - Toate drepturile rezervate