Masurarea indicelui de refractie a unui esantion prismatic

Masurarea indicelui de refractie a unui esantion prismatic

1 Prisma optica. Definitii. Relatii specifice. Exprimarea unghiului de deviatie optica in prisma

Spre deoseride de o lamela cu fetele plan paralele, care este un sistem de doi dioptri plan paraleli, prisma optica este un sistem de doi dioptri plani ale caror suprafete plane nu sunt paralele, ci fac un unghi diedru nenul. De regula se alege acelasi mediu in afara unghiului diedru. Unghiul diedru se numeste unghiul refringent, sau pur si simplu unghiul prismei, iar intersectia celor doua suprafete plane ale dioptrilor determina asa zisa muchie a prismei. Sectiunea prismei intr-un plan normal pe muchie se numeste sectiune principala in care se si plaseaza razele incidente si implicit cele emergente si intermediare. Marginirea completa a prismei fata de mediul de imersie implica de fapt si prezenta unui nou dioptru plan, (baza prismei, opusa unghiului diedru a prismei , A), de care putem face abstractie in conditii de emergenta si incidenta numai pe planele adiacente muchiei. In Fig 8 este reprezentata refractia succesiva a unei raze incidente localizata intr-o sectiune normala a prismei. Consideram prisma imersata in aer.

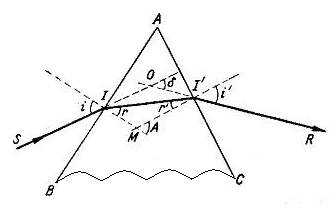
Figura 8

Deoarece materialul prismei este mai refringent decat aerul, refractia in I la trecerea luminii din aer in prisma se face cu apropierea razei de normala, iar refractia in I' la trecerea din prisma in aer se face cu departarea acesteia de normala.

Unghiul de deviatie in prisma notat cu δ, sau simplu, deviatia in prisma este, prin definitie, unghiul dintre raza incidenta si raza emergenta, ambele luate cu directiile si sensurile de propagare. δ este unghi exterior in triunghiul OII' in care unghiurile din I si I', nealaturate lui δ au valorile i- r, respectiv i'-r' rezulta astfel relatia

δ = i - r + i' - r' = i + i'- (r + r')    (31)

Pe de alta parte , in patrulaterul AIMI' unghiurile din I si I' sunt drepte si deci au suma egala cu π; suma tuturor unghiurilor din patrulater fiind 2 π rezulta ca unghiul din M al patrulaterului este suplementul unghiului prismei A. Acelasi unghi este si suplementul celuilalt unghi din M, esterior patrulaterului si triunghiului MII'. Acest unghi exterior este deci congruent cu A. Unghiurile din triunghiul MII' nealaturate lui A sunt r si r' astfel ca se optine relatia specifica prismei,

A = r + r',    (32)

care substituita in ecuatia 31 conduce la urmatoare exprimare a deviatiei

δ = i + i' - A    (33)

Legea a doua a refractiei aplicata in punctele I si I' furnizeaza inca doua relatii independente si anume:

sin i = n sin r    (34)

sin i' = n sin r'    (35)

Relatiile independente 3,3,3 si 3 in care sunt prezente 7 marimi permit exprimarea deviatiei δ numai prin i, n si A.

2 Valoarea minima a unghiului de deviatie

Pentru o prisma specificata N si A sunt fixate si deci deviatia δ depinde numai de unghiul de incidenta i. Se poate arata ca δ, ca functie de unghiul de incidenta, are un singur punct de extrem, mai precis un punct de minim. Pentru a determina valoarea lui i pentru care se realizeaza deviatia minima, trebuie sa rezolvam ecuatia care exprima anularea primei derivate a acestei functii in raport cu variabila i,

    (36)

si care exprima conditia necesara de extrem. Pentru simplitate rezolvam ecuatia anterioara fara a determina explicit δ ca functie de i, sau i' ca functie de i.

Plecam de observatia ca relatia (35) permite exprimarea derivatei prin derivata , iar aceasta se exprima simplu prin . Intr-adevar, daca derivam relatia 32, cu A -constant, obtinem

    (37)

La randul ei derivata se poate construi derivand ecuatia 34 in raport cu i.

Urmand pasii specificati anterior, se obtine succesiv:

, (38)

; (39)

, (40)

Conditia necesara de extrem (36) capata acum forma :

(41)

Pe de alta parte din relatiile (34,35) rezulta simplu o relatie similara in care in locul functiilor cos apar functii sin:

    (42)

Daca avem in vedere ca mediul prismei si mediul de imersie sunt diferite trebuie sa impunem conditiile r ≠ i si r' ≠ i', (mai precis r < i, r' < i', daca n₂ > n₁ ) In plus nu se pot realiza egalitatile r' = i, r = i', care se induc reciproc pe baza ecuatiilor anterioare, deoarece atunci am obtine relatia r + r' = i + i' care ar contrazice ultimele inegalitati.

Conditia necesara de extrem (41) impreuna cu conditia (42) pot fi satisfacute numai daca:

i = i',    r = r' (43)

(Aceasta solutie evident posibila a conditiei de extrem pentru deviatie, (41), devine unica in prezenta conditiei suplimentare (42) induse de legile refractiei in punctele I, I').

In aceste conditii ecuatiile (32) si (34) permit determinarea completa a solutiei de extrem:

r = r' ; , , (44)

(Conditia naturala pentru ca a doua ecuatie (44) care descrie deviatia minima sa admita solutii implica , unde este unhiul limita pentru perechea (mediul prismei, mediul de imersie). Deducem de aici conditia specifica de emergenta pentru o raza care intra in prisma si anume sau , echivalent, A).

Se poate arata ca solutia anterioara de extrem este unica si corespunde unei valori minime a deviatiei. Conform ecuatiei (33) deviatia minima capata valoarea

    (45)

Forma solutiei de extrem (43) ne arata ca deviataia minima se realizeaza pentru un mers simetric al razei, cand aceasta si intersectiile fetelor prismei cu planul sectiunii normale formeaza un trinunghi isoscel cu varful pe muchia prismei.

Solutiile anterioare , date de ecuatiile (44) au fost determinate complet in functie de elementele prismei, A si n, presupunand ca aceste elemente sunt cunoscute.

3 Determinarea indicelui de refractie al unei prisme prin metoda deviatiei minime

3.1 Principiul metodei

Conform legii a doua a refractiei, cand variaza i si implicit r raportul dintre sinusul unghiului de incidenta si sinusul unghiului de refractie ramane constant, reprezentand indicele de refractie al prismei fata de mediul de imersie (aer). Astfel daca se cunoaste unghiul de refractie pentru o incidenta data atunci se poate determina indicele de refractie. In particular indicele de refractie este determinat si de raportul:

    (46)

unde este incidenta la care se realizeaza deviatia minima si pentru care unghiul de refractie este

Daca indicele de refractie al prismei este necunoscut nu putem determmina prin ecuatia (44). Conform ecuatiei (45) pentru deviatia minima deducem ca unghiul care nu poate fi calculat cu ajutorul ultimeia din ecuatiile (34) deoarece nu se cunoaste indicele de refractie al prismei, poate fi determinat daca se masoara experimental deviatia minima si eventual unghiul prismei (daca acesta nu este cunoscut).

Din relatia (45) rezulta

(47)

si se poate determina indicele de refractie al prismei in functie de deviatia minima si unghiul prismei,

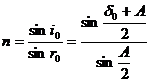    (48)

Instalatia si procedurile de masurare a unghiului prismei si a deviatiei minime sunt descrise in lucrarea de laborator aferenta prezentei teme; in esenta aceste marimi se masoara cu ajutorul goniometrului.

Goniometrul este compus dintr-un cerc gradat pe care poate glisa luneta, orientata mereu radial in cursul rotatiei acesteia in jurul centrului cercului gradat. Deplasarile lunetei pot fi masurate cu precizie cu ajutorul unui vernier atasat acesteia. Pe cercul gradat se afla si colimatorul cu sursa de lumina, orientat tot radial.

In zona centrului cercului gradat se afla o masuta care se poate roti in jurul unui ax vertical care trece prin centrul cercului. Pe masuta se plaseaza prisma cu muchia perpendiculara pe planul masutei.

3.2. Masurarea unghiului prismei

Pentru masurarea ungiului prismei se deplaseaza ocularul lunetei pana se vad clar firele reticulare. Se pune apoi luneta la punct la infinit, adica se regleaza pentru vederea clara a unui obiect foarte indepartat. In acord cu notatiile din Fig. (9), care contine sectiunea principala a prismei, se plaseaza prisma cu muchia in centrul O al masutei astfel ca bisectoarea unghiului A al prismei (din sectiunea principala iluminata) sa fie, cu o buna aproximatie, in prelungirea razelor provenite de la colimatorul C.

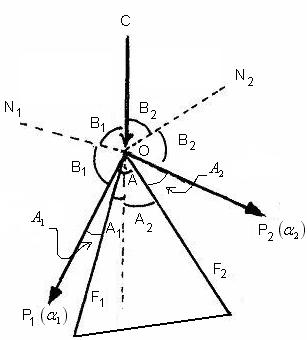
Figura (9)

Se deplaseaza luneta in pozitia P_1, (P₂) in care se vede clar, la intersectia firelor reticulare, imaginea fantei colimatorului C obtinuta cu razele acestuia care se reflecta pe fata F_1, (F₂), citindu-se pe cercul goniometrului diviziunea unghiulara corespunzatoare , .

Se deduce din figura ca modulul diferentei celor doua diviziuni reprezinta dublul unghiului prismei, , chiar daca axa colimatorului nu este riguros orientata pe directia bisectoarei unghiului prismei. Intr-adevar, raza CO este inclinata sub unghiul A₁, (A₂), in raport cu fata F₁, (F₂), astfel ca raza OP₁, (OP₂), reflectata pe aceasta fata face acelasi unghi cu F₁, (F₂). In consecinta unghiul total dintre razele reflectate OP₁ si OP₂ este 2A₁ + 2A₂ = 2A. In figura (9) F₁ si F₂ sunt fetele prismei care se intersecteaza in muchia proiectata in O, ON₁ si ON₂ sunt normalele la cele doua fete, CO este directia fasciculului de raze incident provenit de la colimator, iar OP₁ si OP₂ sunt fasciculele generate de reflexia pe fetele F₁ si F₂ a fasciculului CO.

3.3. Masurarea deviatiei minime

Pentru determinarea deviatiei minime , se plaseaza prism ape masuta goniometrului astfel ca bisectoarea unghiului A al prismei sa fie aproximativ perpendiculara pe directia razelor care vin de la collimator. Mentinandu-se colimatorul fixat, se adduce luneta intr-o pozitie care sa permita observarea imaginii fantei data de lumina refractata prin prisma. Se lucreaza cu o lampa cu mercur, astfel ca se observa mai multe linii in fanta din cauza dispersiei luminii in prisma. Rotind incet masuta cu prisma in acelasi sens, se constata deplasarea imaginii fantei in campul lunetei, oprirea momentana si apoi schimbarea sensului deplasarii. Rotind foarte incet masuta in sens invers si din nou in sensul initial, se fixeaza luneta in pozitia P₁' la diviziunea in care imaginea fantei tindea sa se opreasca. Pentru aceasta configuratie se realizeaza deviatia minima. Se roteste acum masuta cu aproximativ 180° fata de pozitia initiala si se identifica in acelasi mod pozitia lunetei in pozitia P₂^' la diviziunea in care deplasarea imaginii tindea sa-si schimbe sensul. Determinarile se fac pentru o linie spectrala aleasa pe care se fixeaza intersectia firelor reticulare ale lunetei. Deoarece colimatorul si implicit raza incidenta au ramas fixate la directie, rezulta ca cele doua pozitii ale lunetei in care se realizeaza deviatia minima sunt separate de un unghi egal cu dublul deviatiei minime.

    (40)

Bibliografie

1. Optica, fizica plasmei, fizica atomica si nucleara pentru perfectionarea profesorilor, Ed. Didactica si Pedagogica, Bucuresti 1983
2. G.C. Moisil, Eugen Curatu, Optica. Teorie si aplicatii, Ed. Tehnica, Bucuresti 1986
3. I.I. Popescu, Optica, I. Optica geometrica, Tipografia Universitatii din Bucuresti, 1988
4. F.Uliu, M.Chiriac, Optica si spectroscopie, Reprografia Universitatii din Craiova 1978
5. M.Ursache, I. Palarie, Masuratori experimentale cu aparatura optica, Editura M.I.M Craiova, 1999
6. M.Chiriac, Optica geometrica - Caiet de lucrari practice Reprografia Universitatii din Craiova, 1976
7. I.Iova L.Nasta, M.Prodan, Optica, Ed.Didactica si Pedagogica, Bucuresti 1973
8. S.Ursu, I.Toma, R.Ionescu, C.Onea, Ghid de lucrari practice pentru laboratorul de fizica, Ed. Radical, Craiova, !996

M. Paula, M.Tutunaru, E.Tugulea, Lucrari practice de optica, Reprografia Universitatii din Craiova, 1988