Acceleratia in miscarea oarecare

Acceleratia in miscarea oarecare

Intr-o miscare oarecare in spatiul, traiectoria este o curba ca si modul cat si ca orientare. Prin urmare, acceleratia care va trebui intotdeauna sa fie orientata spre interiorul curbei oarecare in spatiu, va avea atat o componenta care sa produca variatia modulului vitezei, cat si una care sa ii produca modificarea directiei tn spatiu. Pentru evaluarea acestor componente, se va analiza in primul rand modificarea orientarii vectorului viteza. Pentru aceasta vom considera in fig. 3.4 situatia tangentelor la curba in doua puncte in care se evalueaza viteze.

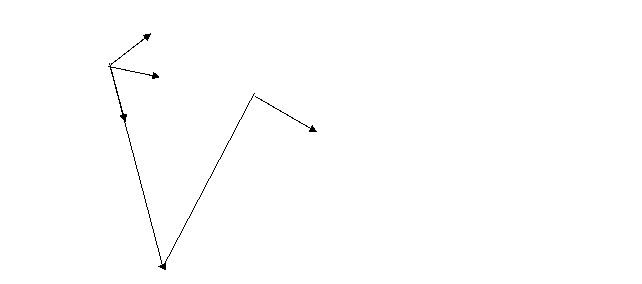
Fig. 3.4. Obtinerea cercului oculator al curbei in punctul P

Pentru a caracteriza directia vitezei in punctul P si P¹, se introduc doi versori ai tangentelor la curba in cele doua puncte: t si t . La limita, daca P¹ → P, portiunea infini.. a curbei din jurul punctului P, poate fi aproximata cu un cerc cu centrul in C, numit cerc osculator al curbei in punctul P, sau cerc de curbura (Doar in acest caz, punctele P si P¹ pot fi considerate aflate intr-un plan ce contine cercul, numit plan osculator. Datorita faptului ca, curba este orientata in spatiu, la un alt moment de timp, orientarea planului osculator se schimba). In aceasta situatie, curbura curbei in punctul P, poate fi aproximata cu curbura cercului osculator cu centrul tn C. Curbura cercului si raza sa de curbura, au expresiile

(3.25)

Pentru evaluarea acceleratiei , se mai introduc versorii.normala prioncipala in punctul P perpendiculara pe tangenta    t si continuta in planul osculator si binormala . obtinuta din cele doua prin constructia unui

.. (3.26)

Pentru a evalua partea din acceleratie care modifica doar orientarea vitezei, vom considera modificarea oreintarii versorilor tangenti la curba. Aceasta modificare este data de vectorul Δt = t - t. Se pune problema evaluarii acestei diferente in functie de gradul de curbura al curbei din spatiu, in punctul P. Pentru aceasta, se va considera

lim .. . tinand cont ca |Δt | = 2 |t| sin . = 2 sin . |t| = 1

lim = lim = lim . = 1     (3.27)

la limita P¹ → P sau Δ .. → 0, versorul t¹ tinde sa devina paralel cu t si atunci Δt va avea directia versorului normal n , astfel incat

lim .. (3.28)

Deoarece t este un vector de modul unitar (versor), o variatie a sa poate doar in urma unei rotatii si la o rotatie infinite.. d, diferentiala acestui versor are modulul egal chiar cu unghiul infiniteyimal de rotatie (|dt| = d ) iar orientarea data de un alt versor, normal pe versorul care variaza (se roteste).

Relatia (3.28) permite enuntarea primei relatii a lui Frenet

(3.29)

Aceasta relatie este utilizata in relatia de definitie (3.22) pentru deducerea expresiei acceleratiei in miscarea pe o traiectorie curbilinie oarecare.

a = ..     (3.30)

Primul termen, reprezinta componenta tangentiala a acceleratiei si el caracterizeaza modificarea modulului vitezei in lungul tangentei la traiectorie

a = .. (3.31)

cel de-al doilea termen poate fi prelucrat convenabil, tn conformitate cu mentiunile precedente referitoare la faptul ca un versor t (de modul constant), poate varia in timp doar prin modificarea orientarii sale, adica prin rotatie

(3.32)

Prin urmare, cel de-al doilea termenal relatiei (3.30) reprezinta o acceleratie normala la traiectorie in punctul considerat

(3.33)

Care are rolul de a produce doar modificarea orientarii vectorului viteza

In concluzie, introducand relatiile (3.31) ai (3.33) in relatia (3.30)

(3.34)

Se observa ca intr-o miscare pe o curba oarecare, iintotdeauna acceleratia care produce modificarea modulului viteza si una universala care produce modificarea orientarii acestuia. Se observa ca si atunci cand viteza pe traiectori ramane constanta (modulul vectorului viteza) daca traiectoria este curbilinie, intotdeauna apare o acceleratie care produce modificarea orientarii vectorului viteza, pentru a-l face in orice punct tangent la traiectorie si aceasta acceleratie este normala pe viteza (de ex. miscarea circulara uniforma)