 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
COMPUNEREA VIBRATIIlor ARMONICE
Obiectivele lucrarii sunt:
Prezentarea notiunilor teoretice legate de compunerea vibratiilor armonice dupa directii ortogonale;
simularea si compunerea vibratiilor armonice folosind subprogramul Simulink din Matlab;
compunerea vibratiilor armonice cu ajutorul unui dispozitiv si trasarea vibratiei rezultante.
2 Consideratii teoretice
1 Compunerea vibratiilor armonice dupa directii ortogonale A. Compunerea vibratiilor ortogonale de pulsatii diferite Se studiaza compunerea vibratiilor ortogonale de pulsatii diferite ale caror ecuatii de miscare sunt:
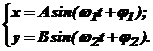 (1)
(1)
Se pot intalni doua situatii:
A1. Traiectoriile sunt curbe inchise;
A Traiectoriile sunt curbe deschise.
A1. Daca traiectoriile se inchid inseamna ca mobilul trece prin acelasi punct dupa un timp minim T, adica :
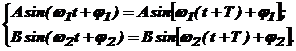 (2)
(2)
Deci, T trebuie sa fie multiplu al celor doua perioade:
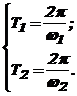
adica :T=k1T1=k2T2
sau: ![]() (3)
(3)
unde : k1 si k2 sunt doua numere intregi.
Rezulta T ca cel mai mic multiplu al perioadelor T1 si T Din relatia (1.44) rezulta :
![]() (4)
(4)
adica
raportul ![]() este un numar rational. Aceasta
reprezinta conditia ca traiectoriile sa se inchida. A In cazul in care traiectoriile sunt deschise, miscarea
punctului nu mai este periodica, iar pulsatiile celor doua
miscari componente nu sunt comensurabile.
este un numar rational. Aceasta
reprezinta conditia ca traiectoriile sa se inchida. A In cazul in care traiectoriile sunt deschise, miscarea
punctului nu mai este periodica, iar pulsatiile celor doua
miscari componente nu sunt comensurabile.
B. Compunerea vibratiilor armonice ortogonale
In continuare, se analizeaza trei
cazuri particulare: B1. -
pulsatiile celor doua miscari sunt egale: ![]() , iar
fazele initiale sunt, de asemenea, egale:
, iar
fazele initiale sunt, de asemenea, egale: ![]() B - pulsatiile celor
doua miscari sunt egale:
B - pulsatiile celor
doua miscari sunt egale: ![]() , iar
fazele initiale nu sunt egale
, iar
fazele initiale nu sunt egale ![]()
B3 - pulsatiile celor doua vibratii armonice ortogonale sunt diferite.
B1. Prin eliminarea timpului intre ecuatiile (1.42) se ajunge la ecuatia :
![]() (5)
(5)
ceea ce reprezinta o dreapta care trece prin originea O a sistemului de coordonate.
Deci, miscarea rezultanta este o vibratie armonica pe un segment din dreapta de ecuatie (1.46).
Amplitudinea miscarii rezultante este data de relatia (fig 1)
![]()
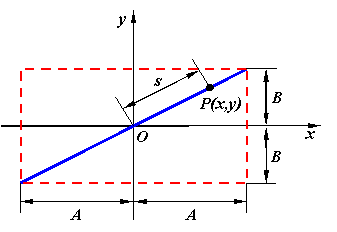
Fig.1 Reprezentarea grafica a compunerii vibratiilor
armonice ortogonale de
pulsatii egale: ![]()
si faze initiale egale: ![]()
Expresia arcului s este: ![]()
B Ecuatiile celor doua miscari se scriu subforma :
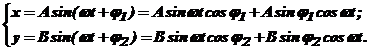 (7)
(7)
Prin rezolvarea sistemului (7) in
necunoscutele ![]() rezulta:
rezulta:

Eliminand timpul t
se obtine ecuatia curbei sub forma urmatoare:![]()
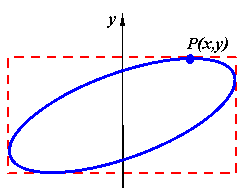
care reprezinta ecuatia unei elipse
fig. Deci, punctul ![]() parcurge aceasta elipsa in
acelasi sens, avand o miscare periodica cu perioada
parcurge aceasta elipsa in
acelasi sens, avand o miscare periodica cu perioada ![]()
x O
![]()
Fig.2 Reprezentarea grafica a compunerii vibratiilor
armonice ortogonale de pulsatii egale: ![]()
si faze initiale diferite: ![]()
B3. In cazul cand pulsatiile celor doua vibratii armonice ortogonale sunt diferite putem avea doua situatii:
pulsatiile ![]() si
si ![]() sunt comensurabile.
sunt comensurabile.
In acest caz traiectoria punctului ![]() este o curba inchisa. In figura 3
s-a reprezentat grafic traiectoria punctului
este o curba inchisa. In figura 3
s-a reprezentat grafic traiectoria punctului ![]() in cazul cand
in cazul cand ![]()
![]()
![]()
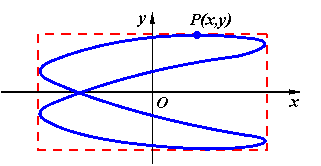
Fig.3 Reprezentarea grafica a compunerii vibratiilor armoni-ce ortogonale de pulsatii comensurabile si faze initiale diferite
pulsatiile ![]() si
si ![]() nu sunt comensurabile.
nu sunt comensurabile.
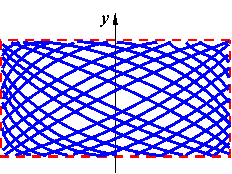
In acest caz miscarea punctului
![]() nu mai este periodica, iar traiectoria nu
se inchide (fig. 4).
nu mai este periodica, iar traiectoria nu
se inchide (fig. 4).
O
![]()
Fig.4 Reprezentarea compunerii vibratiilor armonice ortogonale de pulsatii necomensurabile si faze initiale diferite
3 Echipament de lucru
Dispozitivul de compunere a vibratiilor armonice si trasare a vibratiei rezultante este aratat in figura 5.

Fig.5 Dispozitivul utilizat pentru compunerea si trasarea vibratiei rezultate in urma compunerii a doua
vibratii armonice dupa directii ortogonale
placa de baza;
coloana;
manivela;
ghidaje longitudinale;
ghidaje transversale;
curea;
intinzator de curea;
roata de curea;
9, 10 - bare reglabile;
11 - placa
12 - element trasor (creion);
13 - placa de trasat (hartie
4 Prelucrarea datelor
Pentru simularea
si compunerea vibratiilor armonice cu ajutorul subprogramul Simulink
din Matlab se foloseste urmatoarea schema bloc de generare
si compunere a doua vibratii armonice avand urmatorii
parametrii: ![]() si
si![]() , iar forta perturbatoare
, iar forta perturbatoare ![]() si
si ![]() (fig.6).
(fig.6).
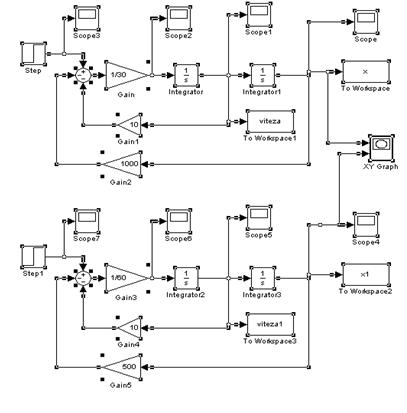
Fig.6 Schema bloc de generare si
compunere a doua vibratii armonice
Folosind schema bloc anterioara se vizualizeaza separat fiecare vibratie si, in final, vibratia rezultata in urma compunerii celor doua vibratii este data de ecranul XY Graph (fig.7).
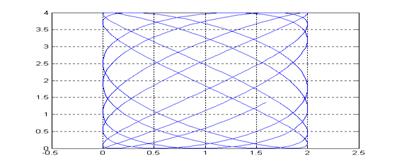
Fig.7
Vibratia rezultata in urma compunerii a doua vibratii armonice
de parametrii ![]() si
si![]()
Folosind aceeasi schema
bloc, dar marind de 2 ori freventa celei de-a doua vibratii se
obtine o vibratie rezultanta ca in fig. 8. 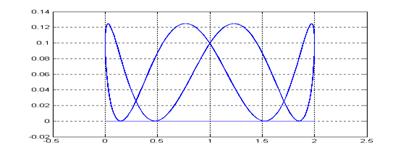
Fig.7
Vibratia rezultata in urma compunerii a doua vibratii armonice
de parametrii ![]() si
si![]()
5 Concluzii
Copyright © 2025 - Toate drepturile rezervate