 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Functii termodinamice integral molare si de exces
1. Functii integral molare de amestec
O marime integral molara poate fi exprimata cu relatia:
![]()
in care:
![]() si
reprezinta marimea corespunzatoare unui mol de solutie,
deci:
si
reprezinta marimea corespunzatoare unui mol de solutie,
deci:
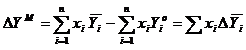
Pentru un sistem binar:
![]()
Marimile partial molare se pot determina functie de marimile integral molare, cu relatia:
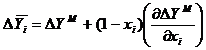
2. Functii si marimi de exces, de amestec
Marimea partial molara de exces de
amestec, (![]() ) corespunzatoare unui component (i), reprezinta
abaterea marimii partial molare de amestec
) corespunzatoare unui component (i), reprezinta
abaterea marimii partial molare de amestec ![]() de la valoarea
corespunzatoare solutiei ideale
de la valoarea
corespunzatoare solutiei ideale ![]() .
.
![]()
Conform definitiei termodinamice marimile
partial molare, de exces ![]() se pot exprima cu relatiile:
se pot exprima cu relatiile:
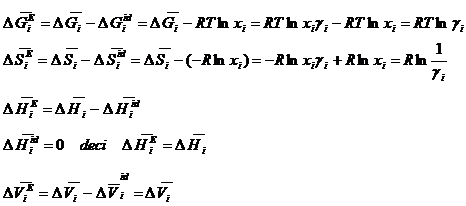
Functiile
termodinamice si marimile integral molare de exces, de amestec (![]() ) se pot determina cu relatiile:
) se pot determina cu relatiile:
![]()
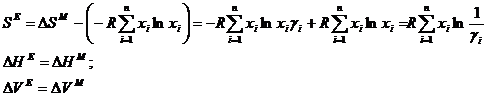
Marimea partial molara de exces a unui component (i), se poate exprima in functie de marimea integral molara de exces a aceluiasi component cu relatia:
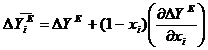
Copyright © 2025 - Toate drepturile rezervate