Feromagnetismul

FEROMAGNETISMUL

FEROMAGNETISMUL

I. Introducere

Odonarea feromagnetica

Un feromagnet are un moment magnetic spontan intr-un moment magnetic chiar intr-un camp magnetic aplicat nul. Un moment spontan sugereaza faptul ca spinii electronici si momentele magnetice sunt aranjate intr-un mod regulat. Ordinea nu trebuie sa fie neaparat simpla: toate arnajamentele de spini sunt schitate in figura 1 cu exceptia antiferomagnetului simplu.

II. Cuprins

Punctul Curie si integrala de schimb

Sa consideram un paramagnet cu o concentratie N de ioni, de spin S, fiind data de interactie interna, care tinde sa alinieze momentele magnetice paralele intre ele, vom avea un feromagnet. Sa postulam o astfel de interactiume si sa o numim camp de schimb sau camp molecular. Efectului de orientare al campului de schimb i se opune agitatia termica si la temperaturi ridicate ordomarea spinilor este distrusa.

Temperatura Curie T_c este temperatura deasupra careia dispare magnetizarea spontana; ea separa faza paramagnetica dezordonata la T > T_c de faza feromagnetica ordonata la T < T_c. Putem gasi pe T_c in functi de . Sa consideram faza parametrica: un camp aplicat B_a va produce o magnetizare finita si aceasta la ramdul ei va produce un camp de schimb finit B_E. Daca este susceptibilitatea,

B_E = λM     {1)

(2)

Susceptibilitatea a unei substante paramagnetice este data de legea lui Curie = C/T, unde C este constanta Curie. Folosind (1) si (2), MT = C (B_a + M) si

= M/B = C/(T - C (3)

Susceptibilitatea are o singularitate pentru T = C . La aceasta temperatura (si sub ea) exista o magnetizare spontana deoarece daca este infinit putem avea un M finit pentru B_a nul. Din (3) rezulta legea Curie - Weiss.

(4)

Campul de schimb da o reprezentare aproximativa interactiei de schimb cuantice. Cu anumite ipoteze se poate arata ca energia de interactie a atomilor i, j avand spinii S_i , S_j , contine un termen

U = - 2J S_i S_j (5)

Unde J este integrala de schimb si este legata de suprapunerea distributiilor de sarcina ale atomilor i si j. Ecuatia (5) se cheama modelul lui Heisenberg.

Distributia sarcinilor intr-un sistem de doi spini depinde de orientarea paralela sau antiparalela a spinilor, deoarece principiul lui Pauli interzice ca doi electromi cu acelasi spin sa fie simultan in acelasi loc. Nu interzice acest lucru pentru doi electroni de spin opus. Astfel energia electrostatica a sistemului va depinde de orientarea relativa a spinilor: diferenta de energie defineste energia de schimb. Energia de schimb a doi electroni se poate scrie sub forma - 2Js₁ s₂, ca si cum ar exista un cuplaj direct intre dirctiile celor doi spini.

Vom stabili o legura aproximativa dintre integrala de schimb J din (5) si constanta de schimb din (1). Presupunem ca atomul considerat are z vecini cei mai apropiati, fiecare legati de atomul central prin interactia J. Pentru vecinii mai departati vom lua J = 0. energia necesara pentru a inversa spinul considerat in prezenta tuturor celorlalti spini poate fi scrisa neglijand componentele lui S perpendiculare pe magnetizarea medie sub forma:

(6)

Unde S este valoarea medie a lui S in directia magnetizarii, iar Ω este volumul de atom

Momentul magnetic mediu al unui spin este μ = gSμ_B Si magnetizarea de saturatie este M_s = μΩ. In modul acesta din (6) rezulta

λ = 2Jz Ω/g² μ²_B (7)

(8)

unde z este numarul vecinilor celor mai apropiati.

Aproximatii mai bune ale problemei statistice cuantice dau rezultate intructva diferite pentru k_BT_c /zJ; pentru structurile cs, cvc si cfc cu S = 1/2, Rushbrooke si Wood dau k_B T_czJ = 0,28; 0,325 si respectiv 0,346, in comparatie cu 0,500 din (8) pentru toate cele trei structuri. Daca fierul este reprezentat prin modelul lui Heisenberg (6) cu S = 1, atunci temperatura Curie observata corespunde lui J = 1,19 . 10 ^-2 eV.

Dependenta de temperatura a magnetizarii de saturatie

Putem folosi de asemenea aproximatia campului molecular sub temperatura Curie pentru a gasi magnetizarea in functie de temperatura. Vom proceda ca si mai inainte, dar in locul legii lui Curie vm folosi expresia completa a lui Brillouin (15.20)pentru magnetizare.pentru spini ˝ din aceasta da M = Nμth(μB/k_B T), In concordanta cu (15.20). Daca omitem campul magnetic aplicat si inlocuim pe B cu campul molecular B_E = λM, atunci :

M = Nμth(μλM/k_BT) (9)

Vom vedea ca exista solutii ale acestei ecuatii cu M nenul in intervalul de temperatura intre 0 si T

Pentru a rezolva (9) scriem aceasta ecuatie in magnetizare redusa m = M/Nμ si temperatura redusa t = k_BT/Nμ²λ de unde:

m = th(m/t). (10)

Reprezentam apoi membrul drept si membrul sting al acestei ecuatii separat in functie de m. Punctul de intersectie al celor doua curbe da valoarea lui m, la temperatura care prezinta interes.

Curbele lui M in functie de T obtinute in acest mod reproduc aproximativ trasaturile rezultatelor experimentale. Cand T creste, magnetizarea scade monoton spre zero la T = T_e. Aceasta comportare clasifica tranzitia obisnuita feromagnetic/paramagnetic ca fiind de ordinul doi.

Teoria campului mediu nu da o buna descriere a variafiei lui M la temperaturi joase. Pentru T << T_c argumentul tangentei hiperbolice din (10) este mare si

th 1 - 2e^-2ζ ..    (11)

In ordinul cel mai coborat, abaterea M == M(0) - M(T) este

M ≈ 2N exp(- 2 N /k_BT).   

Argumentul functiei exponentiale este egal cu - 2T_c/T. Pentru T = 0,1 T_c avem M/N ≈ a 2 exp(-20) ≈ 4

Undele de spin

Starea fundamentala a unui feromagnet simplu are toti spinii paraleli ca in figura 1. Sa onsidera N spini, fiecare de marime S pe o linie sau pe un cerc cu spinii cei mai apropiati cuplati prin interactia Heisenberg (6)

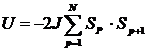
Aici J este integrala de schimb si hS_p este momentul cinetic al spinului in punctul p. Daca tratam spinii S_p ca vectori clasici, atunci in starea funda­mentala S_p . S_p+1 = S² si energia de schimb a sistemului va fi U₀ = - 2NJS².Care este energia primei stari excitate ? Sa consideram o stare excitata cu un anumit spin inversat, ca in figura 1. Se vede din (13) ca aceasta mareste energia cu 8JS², astfel incat U₁ = U₀ + 8/S².

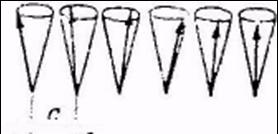
Fig.1 Excitatiile elementare coborite sunt undele de spin. Extremitatile vectorilor spin efectueaza o miscare de precesie pe suprafata unor conuri, cu spinii succesivi avansati ca faza cu un unghi constant.

In componente carteziene

dS²/dt = (2J/h)[S^y_p(S^x_p-1 + S^x_p+1) - S^y_p(S^x_p-1 + S^x_p+1)] (14)

si analog pentru dS^y_p /dt si dS^x_p,/dt. Aceste ecuatii contin produse ale componentelor spinului si sunt neliniare.

Daca amplitudinea excitatiei este mica (daca S^x, S^y_p << S) putem obtine un sir aproximativ de ecuatii liniare luand toti S^x_P = S si neglijand termenii care contin. produse de S^x si S^y, care apar in ecuatia pentru dS^z/dt. Ecuatiile liniarizate sunt

dS^x_P /dt= (2JS/h) (2 S^y_p(S^x_p-1 + S^x_p+1)    (15 a)

dS^x_p/dt= (2JS/h) (2 S^y_p(S^y_p-1 +S^y_p+1 (15 b)

dS^x_P /dt    (16)

Prin analogie cu problema fononilor, cautam solutii ale lui (15) de forma undelor progressive

unde u, v sunt constante, p este un intreg si a este constanta retelei. Substituind in (15) obtinem:

- i u = (2JS/h) (2 - e ^{- ika} - e ^ika)v = (4JS/h) (1 - cos ka) v

- j v = - (2JS/h) - e ^{- ika} - e ^ika) u (4JS/h) (1 - cos ka)u.

Aceste ecuatii au o solutie pentru u si v daca determinantul coeficientilor este egal cu zero

iω    (4/S/h) (1 cos ka) = 0 (18)

- (4JS /h) (1 - cos ka) iω

^;
de unde

hω = 4JS(l -cos ka). (19)

Acest rezultat este reprezentat in figura 2. Cu aceasta solutie gasim ca v = - iu, corespunzator precesiei circulare a fiecarui spin in jurul axei z.

Ecuatia (19) constituie relatia de dispersie (k) pentru undele de spin in cazul unidimensional cu interactii intre vecinii cei mai apropiati. Pentru lungimi de unda mari ka << 1, astfel incat (1 - cos ka) ≈ (ka)². In aceasta limita (19) devine:

h ≈ (2JSa²)k²    (20)

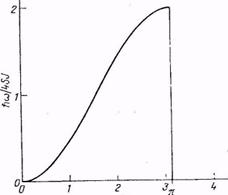
Fig. 2. Relatia de dispersie pentru undele de spin intr-un feromagnet in cazul unidimensional cu interactii intre vecinii cei mai apropiati.

Observam ca frecventa este proportionala, cu k², in timp ce frecventa unui fonon in aceeasi limita, este proportional cu k.

Relatia de dispersie pentru o retea cubica feromagnetica (cs, cvc sau cfc) cu interactii intre cei mai apropiati vecini este urmatoarea, dupa cum sc poate arata

    (21)

unde suma se extinde asupra vectorilor z notati cu care unesc atomul central cu vecinii sai cei mai apropiati. Termenul principal din dezvoltarea lui (21) pentru ka < 1 este

h = (2JSa²)k² (22)

Cuantificarea undelor de spin

Valorile numarului cuantic de spin total al unui sistem de N spini S sunt NS, NS-1, NS-2, conform mecanicii cuantice a momentelor cinetice. In starea fundamentala feromagnetica numarul cuantic de spin total are valoarea NS: toti spinii sunt paraleli in starea fundamentala. Excitarea unei unde de spin micsoreaza spinul total, deoarece spinii nu mai sunt paraleli. Sa cautam relatia dintre amplitudinea undei de spin si reducerea componentei z a numarului cuantic de spin total.

Sa consideram unda de spin cu v = - iu, asa cum am gasit mai inainte

Componenta spinului, perpendiculara pe directia z este u, independent de pozitia punctului p si de timp. Componenta z a unui spin este

S_z =(S² - u²)^1/2 ≈ S - u²/2S (24)

pentru amplitudini mici u/S <

Teoria cuantica permite numai valori intregi pentru S - S_z.

Daca N este numarul total de spini si NS - n_k este numarul cuantic de spin total atunci cand este excitata o unda de spin k, din (24) rezulta.

n_k ≈ Nu²_k /2S sau n² _k ≈ 2Sn_k/N    (25)

Ecuatia (25) reprezinta conditia de cuantificare pentru amplitudinea undei de spin u_k in aproximatia noastra semiclasica. Numim n_k, numarul de magnoni, de vector de unda k, care sunt excitati. Fiecare magnon micsoreaza componenta z a spinului total cu o unitate.

Energia de schimb depinde de cosinusul unghiului dintre spinii din punctele p si p + 1. Diferenta de faza in acelasi mo­ment t intre spinii succesivi este ka radiani, conform lui (23). Varfurile a doi vectori spin din figura 3 sunt separate printr-o distanta 2u sinka, astfel incat unghiul dintre vectorii-spin este dat de

    (26)

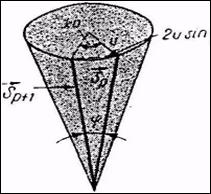
Fig. 3. Constructia care leaga unghiul dintre doi vectori-spin succesivi de amplitudinea u a undei de spin si de un­ghiul de faza ka. Lungimea liniei intrerupte este 2u sin ka daca lungimea unui spin este S, atunci

S sin φ ≈ u sinka.

Imprastierea neutronilor: elastica si neelastica

Un foton de raze X sufera actiunea distributiei spatiale a sarcinii electronice indiferent daca densitatea de sarcina este magnetizata sau nu. Dar un neutron vede doua aspecte ale unui cristal: distributia nucleelor si distributia magnetizarii elec­tronice.

.Momentul magnetic al neutronului interactioneaza cu momentul mag­netic al electronului. Sectiunea eficace pentru interactia neutron-electron este de acelasi ordin de marime ca pentru interactia neutron-nucleu. Difractia neutronilor pe un cristal magnetic permite determinarea distributiei, directiei si ordonarii momenteleor magnetice. Mai departe, un neutron poate fi imprastiat neelastic de structura magnetica, cu crearea sau anihilarea unui magnon: astfel de evenimente fac posibila determinarea experimentala a spectrului magnonic.

Momentele magnetice asociate cu componente particulare ale aliajelor pot fi investigate cu ajutorul difractiei neutronilor.

Intr-un proces de imprastiere neelastica un neutron poate crea sau distruge un magnon (fig. 4). Daca neutronul incident are vectorul de unda k_n si este imprastiat cu k'cu crearea unui magnon de vector de unda k, atunci in baza conservarii impulsului cristalin

k_n = k'_n + k + G (27)

Fig. 4. Imprastierea unui ueutron cu crearea unui magnon.

unde G este un vector al relatiei reciproce. In baza conservarii energiei

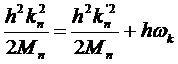    (28)

unde h _k este energia magnonului creat in proces. Curbele de dispersie ale magnonilor pot fi deosebite experimental de curbele de dispersie ale fononilor in acelasi cristal datorita a doua trasaturi distincte: (1) magnonii dispar (sau cel putin drumul lor liber mijlociu devine foarte scurt) la temperaturi putin peste temperatura Curie. (2) Intensitatea imprastierii neutronilor de catre magnoni este proportionala, cu patratul acelei componente a spinului probei care este perpendiculara pe vectorul de imprastiere al neutronului k_n'-k_n, dupa cum este demonstrat in QTS, p. 380-382. Astfel intensitatile relative ale imprastierii inelastice a fononilor si magnonilor pot fi variate printr-o rotire convenabila a probei putandu-se astfel identifica cu certitudine magnonii.

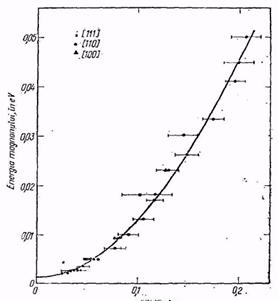
Fig. 5. Spectrul magnonic al unui aliaj de cobalt cfc (92 Co 8 Fe) la temperatura camerei, dupa R. N. Sinclair si B. N. Brockhouse. Phys. Rev., 120, 1638 (1960). Linia plina. este cea mai buna aproximare a curbei teoretice. Rezultatele aratate nu se extind prea departe in zona Brillouin

Ordonarea ferimagnetica

In multe cristale feromagnetice magnetizarea de saturatie laT = 0°K nu corespunde unei alinieri paralele a momentelor magnetice ale ionilor paramagnetici constituenti chiar in cristalele pentru care exista o dovada puternica a faptului ca ionii paramagnetici individuali au momentele lor magnetice normale. Cel mai familiar exemplu este magnetita, Fe₃O₄ sau FeO . Fe₂0₃. Astfel, fiecare ion trebuie sa contribuie cu 5 _B la momentul de saturatie. Ionii ferosi (Fe²⁺) au un spin egal cu 2 si trebuie sa contribuie cu 4 _B, in afara de orice contributie a momentului orbital rezidual. Astfel, numarul efectiv de magnetoni Bohr per formula Fe₃0₄ trebuie sa fie aproximativ 2 x 5 + 4 = 14, daca toti spinii ar fi paraleli. Valoarea observata este 4,1. Aceasta discrepanta se explica daca momentele ionilor Fe³⁺ sunt antiparalele intre ele: atunci momentul observat apare numai de la ionul Fe⁺⁺. Rezultatele difractiei neutronilor concorda cu acest model.

O discutie sistematica a consecintelor acestui tip de ordonare a spinilor a fost data de L. Neel, cu referire la o clasa importanta de oxizi magnetici, cunoscuti sub numele de ferite . Termenul ferimagnetic a fost inventat initial psntru a descrie ordonarea feromagnetica a spinilor de tipul feritei si, prin extensiune, termenul acopera aproape oricare compus in care anumiti ioni au un moment antiparalel cu momentul altor ioni. Multi ferimagneti sunt slab conductori de electricitate, o calitate care este exploatata in dispozitivele practice.

Feritele cubice au structura cristalina de tipul spinelului aratata in figura 6. Sunt 8 pozitii tetraedrice (sau A) ocupate si 16 pozitii octaedrice (sau B) ocupate intr-un cub elementar. Constanta retelei este de aproximativ 8 Ǻ. O trasatura remarcabila a spinelilor este faptul ca toate interactiile de schimb (AA, AB si BB) se pare ca favorizeaza alinierea antiparalela a spinilor legati prin interactie. Dar interactia AB este cea mai puternica, astfel ca spinii A sunt paraleli intre ei si spinii B sunt paraleli intre ei, asa fel incit spinii A sa poata fi antiparaleli cu spinii B. Presupunem ca toate integralele de schimb J_AA, J_AB si J_BB sunt negative.

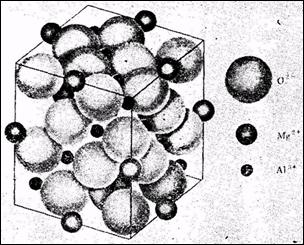
Fig.5. Structura cristalina a mineralului spinel Mg.Al₂O₄; ionii Mg⁺⁺ ocupa pozitii tetraedrice.fiecare inconjurat de 4 ioni de oxigen; ionii A1³⁺ ocupa pozitii octaedrice, fiecare incoujurat de 6 ioni de oxigen. Acesta este un aranjament spinel normal: ionii de metal bivalent ocupa pozitiile tetraodrice. In aranjamentul spinel invers, pozitiile tetraedrice sunt ocupate de ionii de metal trivalent, in timp ce pozitiile octaedrice sunt ocupate jumatate de ioni de metal bivalent si jumatate de ioni de metal trivalent.

III. Concluzii

1. Susceptibilitatea unui feromagnet deasupra temperaturii Curie are forma χ = C/(T - T_c] in aproximatia campului mediu.

2. In aproximatia campului mediu, campul magnetic efectiv ce actioneaza asupra unui moment magnetic intr-un cristal feromagnetic este B_a + M, unde si B_a este cimpul magnetic aplicat.

Intr-un cristal feromagnetic excitatiile elementare sunt magnonii. Relatia lor de dispersie pentru ka < 1 este de forma h = Jk²a² in camp magnetic extern nul. Excitarea termica a magnonilor conduce la o capacitate calorica la temperaturi joase si la o modificare a variatiei relativa a magnetizarii proportionale cu T^3/2

Bibliografie

G. T. Rado si H. S h u 1, eds., Magnetism, Academic Press, 1963, mai multe volume (O lucrare enciclopedica).

S.    Chikazumi Physics of magnetism, Wiley, 1964 (Explicatie elementara a feromagnetismului).

A. H. M o r r i s h, Physical principles of magnetism, Wiley, 1965.

K. M. Bozorth, Ferroinagnetism, Van Nostrand, 1951.

C. K i t t e 1 si J. K. Galt, ,,Ferromagnetic domains', Solid state physics,

D. J. Craik si R. S. T e b b 1 e, Ferromagnetism and ferromagnetic domains, North Holland.

J. Smit si H. P. J. W i j n, Ferrites, Wiley, 1959.

F. K e f f e r, ,,Spin waves', Encyclo. of physics, 18/2 (1966).

T.. N a g a m i y a, K. Yosida si R. K u b o, ..Antiferromagnetism', Adv. in Physics, 4,

J. B. G o o d e n o u g h, Magnetism and the chemical bond, Interscience, 1963.

D. C. M a t t i s, Theory of magnetism, Harper & Row, 1965.

A. H e r p i n, Theorie du magnetisme, Presse Universitaire, 1968.

B. Lax and K. J. Button, Microwave ferrites and ferrimagnetics, Mc Graw-Hill. 1962.