Geodezie si Cartografie

Cartografie matematica

Intocmire si redactare de harti

C. Cuprinsul lucrarii

Proiectia formatul si nomenclatura hartilor si planurilor topografice intocmite si redactate in proiectia stereografica

Intocmirea schemei de impǎrtire si numerotare ale foilor hartii si planurilor la scarile din teritoriul administrativ al comunei Barnova judetul Iasi.

Transformarea coordonatelor geografice ,λ) ale colturilor trapezului geodezic de pe elipsoidul de referinta Krasovski-1940 in coordonate rectangulare plane stereo (x, y)-1970, prin metoda coeficientilor constanti pe baza nomenclaturii

Calculul dimensiunii si ariei trapezului geodezic de pe suprafata elipsoidului Krasovski-1940, corespunzator scarii

Calculul dimensiunii si ariei trapezului din planul sistemului de proiectie stereografica (x,y)-1970 la scara

Calculul deformatiilor liniare si areolare din cadrul foii de plan la scara 1 :5 000, in proiectia stereografica (x,y)-1970

Raportarea si verificarea cadrului interior al originalului de teren al foii de plan la scara 1 :5 000.

Trasarea cadrului geografic si ornamental al originalului de teren al planului topografic la scara

Trasarea retelei rectangulare kilometrice pe originalul de teren al planului topografic la scara

Raportarea punctelor de baza ale retelei geodezice de planimetrie si nivelment

Raportarea punctelor retelei de ridicare si de detaliu ale unui corp de proprietate

Reprezentarea elementelor de planimetrie ale planului cadastral la scara 1 :5 000.

Cartografierea originalului de teren al planului cadastral la scara

Intocmirea planului de amplasament si limitare cadastrala al unui corp de proprietate la scara

Verificarea lucrarilor de intocmire si redactare a originalului de teren al foilor de plan la scarile 1 :5 000 si 1 :1 000.

A. Tema lucrarii:

Pentru introducerea lucrarilor de cadastru general in teritoriul judetului Iasi, care cuprinde o suprafata totala de 547558 ha, incluse in 89 de teritorii administrativ-cadastrale, se cere sa se efectueze calculul bazei cartografice necesare pentru intocmirea si redactarea planului cadastral la scara 1:5000 sub forma digitala sau analogica pe suport de hartie, de material plastic transparent sau baza de date.

In prezent teritoriul administrativ al judetului Iasi cuprinde :

2 municipii - Iasi, Pascani

2 orase - Harlau, Targu-Frumos

85 comune, in care sunt incluse 420 de sate

In vederea intocmirii bazei cartografice a originalelor de teren se vor efectua operatii de calcul, de raportare si de cartografiere in Sistemul Proiectiei Stereografice 1970, avand la baza elementele geometrice ale elipsoidului de referinta Krasovski.1940 si planul de referinta pentru cote Marea Neagra 1975.

Lucrarea practica de cartografie va cuprinde incadrarea teritoriului administrativ-cadastral Barnova in foile de plan la scara 1:5 000 si calculul, intocmirea si redactarea originalului de teren al unei foi de plan cadastral la scara 1:5 000 cu nomenclatura : L-35-32-C (Barnova)-a-4-IV.

B.       Datele lucrarii practice

1. Sistemul de impartire si numerotare al foilor de harta cadastrala la scara 1:50.000 din teritoriul jud. Iasi si zonele limitrofe (26 foi) - fig.1.0.

2. Nomenclatura foilor de harta la scara 1:50.000 ce incadreaza teritoriul administrativ al jud. Iasi

L-35-18-C - (Dolhasca)

L-35-18-D - (Harlau)

L-35-19-A - (Zlatunoaia)

L-35-19-B - (Calarasi)

L-35-19-C - (Focuri)

L-35-19-D - (Perieni)

L-35-20-C - (Trifesti)

L-35-30-A - (Pascani)

L-35-30-B - (Todiresti)

10 L-35-30-C - (Urecheni)

11 L-35-30-D - (Sabaoani)

12 L-35-31-A - (Tg. Frumos)

13 L-35-31-B - (Podu Iloaie)

14 L-35-31-C - (Oteleni)

15 L-35-31-D - (Voinesti)

16 L-35-32-A - (Victoria)

L-35-32-B - (Bosia)

L-35-32-C - (Iasi)

L-35-32-D - (Comarna)

L-35-33-C - (Salageni)

L-35-43-A - (Tansa)

L-35-43-B - (Negresti)

23 L-35-44-A - (Dobrovat)

L-35-44-B - (Raducaneni)

L-35-44-C - (Valeni)

L-35-45-A - (Podolenii)

3. Coordonatele geografice ale colturilor trapezului la scara 1:5.000 cu nomenclatura:

L-35-32-C-a-4-IV

Din teritoriul cadastral Barnova.

4. Incadrarea teritoriului cadastral Barnova in foile hartii cadastrale 1:50.000

5. Elementele de planimetrie, hidrografie si toponimie ale teritoriului Barnova la scara 1:50.000

D. Rezolvarea lucrarii

1. Proiectia, formatul si nomenclatura hartilor si planurilor topografice intocmite si redactate in proiectia stereografica 1970

1.1.Consideratii generale asupra proiectiei stereografice -1970

Proiectia azimutala perspectiva stereografica oblica conforma, cu planul de proiectie secant unic 1970, fiind denumita si "Proiectia STEREO-70", a fost folosita incepand cu anul 1973 la intocmirea planurilor topografice de baza la scarile 1:2 000, 1:5 000, 1:10 000, precum si a hartii cadastrale la scara 1:50 000. Acest sistem de proiectie s-a adoptat, avand la baza elementele elipsoidului Krasovski-1940 si planul de referinta pentru cote Marea Neagra-1975.

La adoptarea proiectiei stereografice-1970 s-au avut in vedere o serie de principii, care satisfac atat cerintele de precizie, cat si avantajele reprezentarii cartografice, din care se mentioneaza:

Teritoriul de reprezentat are o forma aproape rotunda, ce poate fi incadrat intr-un cerc cu raza de circa 300 km.;

Suprafata teritoriului Romaniei se poate reprezenta pe un singur plan de proiectie, obtinandu-se un sistem unic de coordonate plane rectangulare, cu originea in punctul central al proiectiei;

Suprafata terestra se proiecteaza dupa legile perspectivei liniare, in cazul proiectiilor azimutale perspective stereografice oblice, cu latitudinea punctului central al proiectiei φ cuprinsa intre 0 si 90 ;

Proiectia fiind conforma (ώ = 0), indeplineste conditiile de simetrie fata de meridianul de longitudine λ₀ al punctului central.

Deformarile liniare si areolare din planul secant al proiectiei nu influenteaza precizia elementelor reprezentate pe planurile topografice de baza la scarile 1:2000,1:5000, 1:10000;

Valorile deformatiilor liniare si areolare, ce se produc pe planul secant unic la marginile teritoriului Romaniei au fost analizate in vederea optimizarii lor, in cazul distantelor de 275 km, 300 km si 380 km dintre centrul de proiectie Q₀ (φ₀, λ₀) si punctele extreme;

Distantele masurate de la centrul de proiectie la punctele extreme, incadreaza in cea mai mare parte ( 90 %) limitele de hotar ale tarii noastre in cercuri cu raza de 280-300 km, iar cele maxime sunt la circa 380 km la Beba Veche, Mangalia si Sulina;

Deformarile liniare negative ce se produc in centrul de proiectie sunt aproximativ egale cu deformarile liniare pozitive de la marginile zonei de reprezentat;

Deformarile areolare negative si pozitive trebuie sa fie relativ egale si sa se compenseze, adica prin reprezentarea teritoriului considerat in planul de proiectie sa fie mentinuta valoarea suprafetei totale a tarii noastre.

In etapa actuala de introducere a lucrarilor de cadastru general si de publicitate imobiliara, in baza prevederilor din Legea nr. 7/1996, se preconizeaza efectuarea de noi masuratori geodezice si topografice, care sa asigure cartografierea completa si exacta a teritoriilor cadastrale.

1.2. Elementele caracteristice ale proiectiei stereografice-1970

Sistemul de proiectie stereografic-1970 are la baza principiile si formulele aplicate si in sistemul de proiectie stereografic-1930, ce au fost definite de geodezul francez H. Roussilhe, in anul 1924. Parametrii proiectiei stereografice -1970 au fost determinati in functie de elementele elipsoidului de referinta, de pozitia punctului central Q ₀(φ₀, λ₀), si de adancimea planului secant unic fata de planul tangent din punctul central.

Proiectia stereografica-1970, fiind o proiectie azimutala perspectiva oblica conforma, pe plan secant, care pastreaza nedeformate unghiurile, dar deformeaza radial lungimile si suprafetele, prezinta urmatoarele elemente caracteristice:

a. Punctul central al proiectiei

Punctul central al proiectiei este un punct fictiv ( nematerializat pe teren ), fiind situat aproximativ in centrul geometric al Romaniei, la Nord de orasul Fagaras, cea ce permite incadrarea teritoriului Romaniei de reprezentat intr-un cerc cu raza de 400 km.,care din punct de vedere principial satisface cerintele optime ale reprezentarii cartografice (fig. 1.1.) .

Coordonatele geografice ale punctului central al proiectiei, denumit si polul proiectiei Q₀ (φ₀, λ₀), sunt urmatoarele:

φ₀ = 46s 00' 00'', 000 LATITUDINE NORDICA

λ₀ = 25s 00' 00'', 000 LOGITUDINE EST GREENWICH.

b.      Elipsoidul de referinta

Elipsoidul de referinta Krasovski-1940, care s-a folosit in proiectia Gauss, in perioada 1951-1973, a fost mentinut si in proiectia stereografica-1970, fiind orientat la PULKOVO (RUSIA) si avand urmatorii parametrii de baza:

• Semiaxa mare:    a = 6 378 245, 000 000 m
• Semiaxa mica:    b = 6 356 863, 018 770 m
• Turtirea geometrica:    α = 0, 003 352 329 869
• Prima excentricitate:    eČ = 0, 006 693 421 623
• Raza medie de curbura: R₀ = 6 378 956, 681m

c. Punctul fundamental al "sistemului de coordonate 1942"

Reteaua geodezica s-a dezvoltat pe baza punctului astronomic fundamental materializat in cadrul Observatorului Astronomic din Pulkovo (Rusia), definit prin coordonatele geografice :

φ _p = 59°46'18'',550 LATITUDINE NORDICA

λ _p = 30°19'42'',090 LONGITUDINE EST GREENWICH

d. Adancimea planului de proiectie secant unic - 1970

In vederea reducerii deformarilor liniare si areolare s-a adoptat planul secant unic -1970, la adancimea H =3189,478 m fata de planul tangent, in punctul central al proiectiei Q₀ (φ₀, λ₀). In urma intersectarii sferei de raza R cu planul secant, a rezultat un cerc al deformatiilor nule, cu raza r₀ = 201,718 km.

e. Deformatiile lungimilor si suprafetelor

Deformatia regionala pe unitatea de lungime (1 km) in planul secant unic - 1970, din punctul central al proiectiei Q₀(φ₀, λ₀), este de -0,25m/km, dupa care scade in valoare negativa pana la distanta de r₀= 201,785 km, unde este nula.

In exteriorul cercului de deformatie nula (d>r), deformatia liniara relativa creste in valoare pozitiva pana la valori de +0,25 m/km la distanta d = 285 km de punctul central al proiectiei si respectiv, pana la +0,637 m/km la distanta de d = 385 km.

Proiectia stereografica - 1970 satisface precizia reprezentarilor in cazul planurilor topografice intocmite la scarile 1:2000, 1:5000, 1:10000, in toate zonele unde deformatia regionala a lungimilor nu depaseste valoarea de +/-0.15 m/km.

f. Sistemul axelor de coordonate rectangulare plane

Originea sistemului (O) reprezinta imaginea plana a punctului central al proiectiei Q₀(φ₀, λ₀), fiind situat aproximativ in centrul tarii, unde :

axa absciselor ( XX') orientata pe directia Nord - Sud reprezinta imaginea plana a meridianului punctului central Q₀, de longitudine λ₀ =25° ;

axa ordonatelor (YY') orientata pe directia Est - Vest reprezinta tangenta la proiectia paralelei punctului central Q₀, de latitudine φ₀ = 46°.

Pentru lucrarile topo-cadastrale si pentru unele calcule cartografice se foloseste sistemul conventional de axe, care a rezultat din translatarea sistemului cu originea in punctul 0(X₀ = 0,000 m si Y₀ = 0,000 m) cu cate +500 000,000 m spre vest si respectiv spre sud, obtinandu-se punctul O' cu X₀ = 500 000,000 m si Y₀ = 500 000,000 m (fig. 1.2.).

g. Modulul sau coeficientul de reducere la scara

Pentru transformarea coordonatelor plane stereografice (X_<70>;Y_<70>) din planul tangent-1970, in planul secant unic-1970, paralel cu cel tangent, precum si pentru alte calcule cartografice, se efectueaza inmultirea acestora cu coeficientul de reducere la scara:

m₀ = C = 1-1/4000 = 0,999 750 000 .

h. Modulul sau coeficientul de revenire la scara

Pentru transformarea inversa a coordonatelor plane stereografice (X_<70>;Y_<70>) din planul secant unic - 1970, in planul tangent- 1970, precum si pentru alte calcule cartografice, se efectueaza inmultirea acestora cu coeficientul de revenire la scara:

C' = 1/C = 1/0,999 750 000 = 1,000 250 063

i. Formatul si nomenclatura foilor hartii si planurilor topografice

In vederea racordarii si utilizarea foilor hartii si planurilor intocmite in proiectia stereografica - 1970 cu cele vechi din proiectia Gauss, s-a mentinut impartirea foilor de harta si de plan pe trapeze, ce sunt limitate de proiectiile meridianelor si paralelelor.

2. Intocmirea schemei de impartire si numerotare ale foilor hartii si planurilor la scarile 1 :50000, 1 :25000, 1 :10000, 1 :5000 din teritoriul administrativ al comunei Barnova, judetul Iasi.

2.1 Nomenclatura foilor hartii si planurilor topografice intocmite in proiectia Stereo -1970

Reprezentarea grafica a unei portiuni din suprafata terestra se face in mod obisnuit pe mai multe foi de harta sau de plan, in functie de scara, de marimea teritoriului si de proiectia folosita. Pentru identificarea foilor hartii si planurilor editate in proiectia Gauss si stereografica 1970, s-a folosit un sistem de numerotare format din litere si cifre ce poarta denumirea de nomenclatura. Din punct de vedere al utilizarii, nomenclatura sau titlul hartii este propriu fiecarei scari si fiecarei proiectii cartografice. Se mentioneaza ca nomenclatura foilor hartii si planurilor topografice intocmite anterior in proiectia Gauss - Kruger s-a mentinut si in actuala proiectie stereografica-1970, cu exceptia foilor de plan intocmite la scara 1:2000, la care s-au modificat dimensiunile trapezului .

2.1.1 Nomenclatura foilor hartii internationale la scara 1:1000000

Nomenclatura foilor hartii internationale la scara 1:1000000 s-a stabilit in functie de impartirea conventionala a intregii suprafete a globului terestru in zone si fuse geografice .

Astfel, prin trasarea de paralele la ecuator din 4s in 4s pe latitudine, s-a realizat impartirea globului in zone geografice, care s-au numerotat cu literele A, B, C, . , V, incepand de la ecuator pana la paralelul de +88s la nord si respectiv, la -88s la sud. In mod asemanator, prin trasarea de meridiane din 6s in 6s pe longitudine s-au obtinut 60 de fuse geografice, care s-au numerotat de la 1 la 60 incepand de la meridianul de 180s (opusul meridianului Greenwich) in sensul de la vest catre est. Deci fiecare foaie de harta la scara 1:1000000 corespunde unui trapez ale carui dimensiuni sunt de 4s pe latitudine si de 6s pe longitudine. Prin aceasta impartire in zone si fuse geografice s-au obtinut cate 1320 de trapeze la scara 1:1000000, pentru fiecare emisfera de nord si de sud

Nomenclatura foii de harta la scara 1:1000000 este formata dintr-o litera ce defineste zona geografica de 4⁰ pe latitudine si dintr-un numar care indica fusul geografic .

Deci foaia de harta la scara 1:1000000 care contine municipiul Bucuresti are nomenclatura L-35. Teritoriul Romaniei este cuprins in cea mai mare parte in foile L-34 si L-35 si partial, in foile K-34 si K-35 la sud si partial, in foile M-34 si M-35 la nord .

Nomenclatura foilor hartilor la scarile 1:500000 1:2000000 si 1:100000

Sistemul de numerotare al foilor de harta la scarile 1:500000, 1:200000 si 1:100000, se obtine pornindu-se de la trapezul la scara 1:1000000, cu dimensiunile 4s * 6s.

Pentru foile de harta la scara 1:500000, trapezul la scara 1:1000000 se imparte in patru parti (2 * 2) , cu dimensiunile de 2s pe latitudine si 3s pe longitudine, iar pe fiecare trapez se numeroteaza cu literele A, B, C, D. Nomenclatura unei foi de harta la scara 1:500000 este formata din nomenclatura trapezului la scara 1:1000000, la care se adauga litera corespunzatoare zonei: L-35-A

Pentru foile de harta la scara 1:200000, trapezul la scara 1:1000000 se imparte in 36 parti (6 * 6), cu dimensiunile de 40s pe latitudine si de 1s pe longitudine, iar fiecare trapez se numeroteaza cu cifrele romane I, II, III, . , XXXVI. Nomenclatura unei foi de harta la scara 1:200000 se compune din nomenclatura trapezului la scara 1:1000000, la care se adauga cifra romana corespunzatoare zonei: L-35-XVII.

Pentru foile de harta la scara 1:100000, acelasi trapez la scara 1:1000000 se imparte in 144 parti (12 * 12), cu dimensiunile de 20s pe latitudine si de 30s pe longitudine, iar fiecare trapez se numeroteaza cu cifrele arabe 1, 2, 3, . , 144. Nomenclatura unei foi de harta la scara 1:100000 cuprinde nomenclatura trapezului la scara 1:1000000, la care se adauga cifra araba corespunzatoare zonei: L-35-125-Bucuresti.

Nomenclatura foilor hartilor la scarile 1:50000 si 1:25000

Pentru determinarea nomenclaturii foilor de harta la scara 1:50000, se considera trapezul la scara 1:100000, cu dimensiunile 20s pe latitudine si de 30s pe longitudine, care se imparte in 4 parti (2 * 2) la scara 1:50000 cu dimensiunile de 10s pe latitudine si 15spe longitudine, ce se noteaza cu literele A, B, C, D.

Nomenclatura unei foi de harta la scara 1:50000 se compune din nomenclatura foii la scara 1:100000 si din litera corespunzatoare zonei : L-35-125-A.

Prin impartirea foii de harta la scara 1:50000 in 4 parti (2 * 2) se obtin trapezele la scara 1:25000, cu dimensiunile de 5′ pe latitudine 7′ 30″ pe longitudine, ce se noteaza cu literele a, b, c, d.

Nomenclatura unei foi de harta la scara 1:25000 se compune din nomenclatura foii la scara 1:50000 si din litera corespunzatoare zonei : L-35-125-A-d.

Nomenclatura foilor de plan la scarile 1:10000, 1:5000 si 1:2000

Pentru planul la scara 1:10000 se imparte foaia de harta la scara 1:25000 in 4 parti (2 * 2) cu dimensiunile 2′ 30″ pe latitudine si 3′ 45″ pe longitudine, care se noteaza cu cifrele arabe 1, 2, 3, 4.

Nomenclatura foilor de plan la scara 1:10000 se compune din nomenclatura hartii la scara 1:25000 si cifra araba corespunzatoare zonei: L-35-125-A-d-1.

Pentru planul la scara 1:5000 se imparte foaia de harta la scara 1:10000 in 4 parti (2 * 2) cu dimensiunile 1′ 15″ pe latitudine si 1′ 52″,5 pe longitudine, iar fiecare trapez se noteaza cu cifrele romane I, II, III, IV.

Nomenclatura foilor de plan la scara 1:5000, se compune din nomenclatura planului la scara 1:10000 si cifra romana corespunzatoare zonei: L-35-125-A-d-1-I.

Pentru planul la scara 1:2000, foaia de la scara 1:5000 se imparte in 4 parti (2 * 2) cu dimensiunile 37″ ,50 pe latitudine si 56″,25 pe longitudine, care se noteaza cu cifrele arabe 1, 2, 3, 4.

Nomenclatura foilor de plan la scara 1:2000 este formata din nomenclatura planului la scara 1:5000 si cifra araba corespunzatoare zonei: L-35-125-A-d-1-I-1.

Se mentioneaza ca in proiectia Gauss s-a folosit pentru planurile topografice intocmite la scarile 1:5000 si 1:2000 un sistem de numerotare derivat din foaia de harta la scara 1:100000.

Astfel, pentru obtinerea nomenclaturii la scara 1:5000, s-a impartit foaia de harta la scara 1:100000 in 256 parti (16 * 16) cu dimensiunile 1′ 15″ pe latitudine si de 1′ 52,5″ pe longitudine. Fiecare foaie de plan obtinuta s-a numerotat cu cifrele arabe 1, 2, . , 256 de la vest spre est si de la nord la sud.

Nomenclatura unei foi de plan la scara 1:5000, se compune din nomenclatura hartii de baza la scara 1:10000, la care se adauga , in paranteza, numarul corespunzator 1, 2, . , 256 al foii de plan considerate, de exemplu: L-35-125.

In continuare, fiecare foaie de plan la scara 1:5000 (1, 2, . , 256) s-a impartit in 9 parti (3 * 3), care reprezinta foile de plan la scara 1:2000, cu dimensiunile de 25″ pe latitudine si de 37″,5 pe longitudine, ce se numeroteaza cu literele a, b, c, d, e, e, f, g, h, i, de la vest spre est si de la nord la sud.

Nomenclatura unei foi de plan la scara 1:2000, se compune din nomenclatura planului la scara 1:5000, la care se adauga , in paranteza, una dintre literele corespunzatoare zonei, de exemplu: L-35-125-(43-b).

Nomenclatura sau titlul foilor hartilor si planurilor intocmite in proiectia stereografica - 1970 sau in proiectia Gauss, se compune din nomenclatura propriu-zisa a trapezului, la care se adauga denumirea celei mai importante localitati sau a celui mai important detaliu topografic, care sunt reprezentate pe harta sau pe planul respectiv, de exemplu: L-35-125-Bucuresti sau L-35-144-Craiova.

Incadrarea teritorial administrativa Barnova din judetul Iasi in foile hartii cadastrale la scara 1:50000 si 1:25000 si in foile planului cadastral la scara 1:10000 si 1:5000

Schema dispunerii si nomenclatura foilor de harta la scara 1:50000 din teritoriul Barnova judetul Iasi

In functie de schema generala a sistemului de impartire si numerotare al foilor de harta la scara 1:50000 din teritoriul administrativ al judetului Iasi se stabileste incadrarea teritoriului Barnova in trapezele corespunzatoare la scara 1:50000 (Figura 2)

Din schema dispunerii si nomenclatura foilor de harta la scara 1:50000 din teritoriu a rezultat incadrarea teritoriului cadastral Barnova in urmatorul trapez cu nomenclatura L-35-32-C-a-4-IV.

Schema dispunerii si nomenclatura foilor de harta la scara 1:25000 din teritoriul Barnova

In functie de schema de incadrare a teritoriului la scara 1:50000 se efectueaza impartirea trapezelor la 50000 in 4 foi (2 * 2) cu dimensiunile

∆φ = 5′ 00′ (pe latitudine)

∆λ = 7′ 30″ (pe longitudine)

Cele 4 foi de harta la scara 1:25000 se noteaza cu primele litere minuscule a, b, c, d, ale alfabetului latin de la vest spre est si de la nord spre sud.(Figura 2).

Nomenclatura unei foi de harta la scara 1:25000 se compune din nomenclatura foii de baza L-35-32-C la scara1:50000 si din litera minuscula rezultata din zona considerata.

Din sistemul de impartire si numerotare al foilor de harta 1:25000 a rezultat incadrarea teritoriului cadastral Barnova in foaia:

L-35-32-C-a-4-IV

Schema dispunerii, nomenclatura si foile de plan la scara 1:10000 din teritoriul Barnova

Prin impartirea trapezului de la scara 1:25000 in cate 4 foi (2 * 2) cu dimensiunile ∆φ = 2′ 30″ si ∆λ = 3′ 45″ ce se noteaza cu cifre arabe 1, 2, 3, 4 de la vest la est si de la nord la sud se obtine nomenclatura foilor de plan la scara 1:10000.

Nomenclatura unei foi de plan la scara 1:10000 se compune din nomenclatura foii de baza L-35-43-A-d la scara 1:25000 la care se adauga cifrele 1, 2, 3, 4 rezultand urmatoarele foi de plan:

L-35-32-C-a L35-32-C-b L35-32- C-c L-35-32-C-d

In final, teritoriul cadastral se incadreaza intr-un numar total de 7 trapeze la scara 1:10000 din care 1 plin si 6 trapeze se cheama plin - gol.

Schema dispunerii si nomenclatura foilor de plan la scara 1:5 000 din teritoriul cadastral Barnova

Pentru obtinerea nomenclaturii foilor de plan la scara 1:5000 se imparte trapezul de la scara 1:10 000 care incadreaza teritoriul dat in 4 foi (2 * 2) cu dimensiunile ∆φ = 1′ 15″ si ∆λ = 1′ 52″ care se noteaza cu cifre romane I, II , III, IV de la vest la est si de la nord la sud. Nomenclatura unei foi de plan la scara 1:5000 se compune din nomenclatura foii de baza la scara 1:10000 la care se adauga cifra I, II, III, IV rezultand din sistemul de impartire de mai sus urmatoarele foi de plan la scara 1:5000 ale teritoriului cadastral Barnova:

L-35-32-C-a-4-I , L-35-32-C-b-2-I , L-35-32-C-d-4-II , L-35-32-C-c-1-IV, L-35-32-C-c-3-II

L-35-32-C-b-4-II , L-35-32-C-a-4-IV , L-35-32-C-a-3-III , L-35-32-C-c-2-III

L-35-32-C-b-4-III , L-35-32-C-d-2-III , L-35-32-C-c-1-I , L-35-32-C-c-4-I

L-35-32-C-b-4-IV , L-35-32-C-d-2-IV , L-35-32-C-c-1-III, L-35-32-C-c-3-I

In cadrul teritoriului cadastral Barnova s-au numerotat un numar total de 17 trapeze la scara 1:5000, din care 1 trapez plin si 16 trapeze plin - gol.

Recapitulatia modului de incadrare a teritoriului administrativ Barnova din judetul Iasi in foile hartilor si planurilor cadastrale la scara 1:50000 . 1:5000

In functie de sistemul de impartire si numerotare al foilor de harta si de plan la scara 1:50000 . 1:5000 se intocmeste o recapitulatie a modului de incadrare cartografica a teritoriului cadastral Barnova care formeaza obiectul introducerii lucrarilor de cadastru general.

Transformarea coordonatelor geografice (φ, λ) ale colturilor trapezelor de pe elipsoidul de referinta Krasovski (1940) in coordonate rectangulare plane stereo 1970 (x, y) prin metoda coeficientilor constanti

3.1. Principiile transformarii coordonatelor geografice in coordonate rectangulare plane stereografice - 1970

Se considera imaginea generala a reprezentarii stereografice si un punct oarecare B situat pe sfera, de coordonate geografice (φ, λ), cu latitudinea izometrica q si proiectia acestuia pe planul tangent, in punctul B′ de coordonate rectangulare x si y.

Coordonatele punctului central al proiectiei Q₀ sunt coordonatele geografice φ₀, λ₀ si latitudinea izometrica q_0. Din punctul Q ≡ V opus polului q₀ se proiecteaza toate punctele de pe sfera pe un plan de proiectie tangent in Q₀ (φ₀, λ₀ , q₀ ) sau pe un plan secant paralel cu planul tangent.

Reprezentarea stereografica realizata dupa legile perspectivei liniare indeplineste urmatoarele conditii:

Corespondenta intre punctele de pe sfera sau elipsoid si cele din planul de proiectie se realizeaza pe baza unei reprezentari conforme;

Meridianul de longitudine λ₀ care trece prin polul Q₀ (φ₀, λ₀) trebuie sa se reprezinte printr-o dreapta ce se considera ca axa xx′, cu sensul pozitiv spre nord, fiind si o axa de simetrie;

Originea O a sistemului de coordonate rectangulare stereografice (x, y) este imaginea plana a polului Q₀ (φ₀, λ₀ , q₀ ) ;

Unui punct oarecare B (φ₀, λ₀, q₀ ) situat pe meridianul central de longitudine λ₀ ii corespunde in planul de proiectie coordonata x_m data de relatia:

X_m = 2R₀ tg

in care: R₀ - raza sferei Gauss la latitudinea φ₀,;

S = β - lungimea unui arc de meridian, cuprins intre paralelele φ si φ₀.

Din punct de vedere teoretic, marimea x_m data de relatia de mai sus prin distanta Q₀ B′ reprezinta raza vectoare ρ a proiectiilor azimutale perspective stereografice (x_m = ρ), iar unghiul (s / R₀) este distanta zenitala a punctului B.

Deoarece reprezentarea in proiectia stereografica este conforma trebuie ca in baza conditiilor Chauchy - Reimann, coordonatele rectangulare plane (x + iy) sa fie determinate de o functie analitica de variabila complexa (q + il), adica:

(x + iy) = f (q + il)

in care: x si y - coordonatele rectangulare plane stereografice ale punctului dat;

q si l - latitudinea izometrica si diferenta de longitudine dintre punctul dat si centrul proiectiei.

Daca se exprima diferentele dintre coordonatele geografice ale punctului B (φ, λ) si ale punctului central Q₀ (φ₀, λ₀) si respectiv intre laturile izometrice q si q₀, se obtine:

∆φ = φ - φ₀ φ = φ₀ + ∆φ

l = λ - λ₀ sau λ = λ₀ + l

∆q = q - q₀ q = q₀ + ∆q

In relatia 3.2 se introduce expresia q = q₀ + ∆q din relatiile 3.3

(x + y) = f [ q ∆q + il) Pentru stabilirea formulelor de calcul a coordonatelor rectangulare plane stereografice (x,y), s-a efectuat dezvoltarea in serie Taylor a termenului [ q ∆q + il) din relatia anterioara, dupa puterile variabilei ∆q + il) in jurul punctului central Q₀ (φ₀, 1=0, q₀), considerat ca origine a sistemului de coordonate rectangulare:

(x + iy) = f(q)₀ + f′(q) ∆q + il) + 1 / 2! f′′(q)₀ ∆q + il)² + 1 / 3! f′′′(q)₀ ∆q + il)³ + .     . + 1 / n! f⁽ⁿ⁾(q)₀ ∆q + il)ⁿ   

Avande-se in vedere ca: f(q₀) = 0 si f(q) = x_m se vor exprima derivatele de ordinul I, II, III, . , n. sub forma:

a₁ = f′(q)₀ = dx_m / dq ; a2 = 1 / 2! f′′(q)₀ = 1 / 2!d²x_m / dq² ;

a₃ = 1 / 3! d³x / dq³ ; . ; an = 1 / n!dⁿx_m / dqⁿ

In urma introducerii notatiilor a₁, a₂, . a_n, din 3.6 si 3.5, rezulta:

(x + iy) = a₁ ∆q + il) + a₂ ∆q + il)² + a₃ ∆q + il)³ + a₄ ∆q + il)⁴+ a₅ ∆q + il)⁵+ a₆ ∆q + il)⁶ Se efectueaza ridicarile la putere din relatia de mai sus, iar dupa separarea partii reale de cea imaginara, se obtine forma generala a coordonatelor (x, y), functie de diferenta de latitudine izometrica (∆q) si de longitudine (l):

X = a₁∆q + a₂∆q² - a₂l² + a₃∆q³ - 3a₃∆ql² + a₄∆q⁴ - 6a₄∆q²l² + a₄l⁴ + a₅∆q⁵-

- 10a₅∆q³l² + 5a₅∆ql⁴ + a₆∆q⁶ - 15a₆∆q⁴l² + 15a₆∆q²l⁴ - a₆∆q⁶ + .

y = a₁l + 2a₂∆ql + 3a₃∆q² l - a₃l³ + 4a₄∆q³l - 4a₄∆ql³ + 5a₅∆q⁴l-

- 10a₅∆q²l³+ a₅l⁵ + 6a₆∆q⁵l - 20a₆∆q³l³ + 6a₆∆ql⁵ + . Pentru stabilirea relatiilor practice de calcul a coordonatelor plane stereografice - 1970 din coordonatele geografice, se parcurg urmatoarele etape de calcul, pornindu-se de la formulele generale. Se efectueaza trecerea de la diferenta de latitudine izometrica ∆q) la diferenta de latitudine geografica (∆φ);

Se calculeaza coeficientii a₁, a₂, . , a_n si c₁, c₂, . , c_n:

a_n = 1/ n!(dⁿx_m / dqⁿ) ; c_n = 1/ n!(dⁿq / dφⁿ)₀

se exprima coeficientii a_ij si b_ij in functie de coordonatele geografice ale punctului central, de forma:

a₁₀ = a₁c₁ ; a₂₀ = a₁c₂ + a₂c₁² ; . ; b₀₁ = a₁ ; b₁₁ =2a₂c₁ ; .

Se scriu formulele de calcul a coordonatelor rectangulare stereografice din planul tangent, pe baza coeficientilor constanti:

X _tg = (a₀₀ + a₁₀ * f + a₂₀ * f² + a₃₀ * f³ + a₄₀ * f⁴ + a₅₀ * f⁵ + a₆₀ * f⁶) * 1,000

+ (a₀₂ + a₁₂ * f + a₂₂ * f² + a₂₃ * f³ + a₄₂ * f⁴) * l² +

+ (a₀₄ + a₁₄ * f + a₂₄ * f²) * l⁴ +

+ (a₀₆) * l⁶ + .

y _tg = (b₀₁ + b₁₁ * f + b₂₁ * f² + b₃₁ * f³ + b₄₁ * f⁴ + b₅₁ * f⁵) * 1

+ (b₀₃ + b₁₃ * f + b₂₃ * f² + b₃₃ * f³) * l³ +

+ (b₀₅ + b₁₅ * f) * l⁵

in care : f = 10^-4∆φ″ = (φ - φ₀)″

fl= 10^-4∆λ″ = (λ - λ₀)″

a₀₀ = 0,000000

a₁₀ = N₀ (1 - η₀² + η₀⁴ - η₀⁶)(10⁴ / ρ″)¹ = 308758,9579813

a₂₀ = 3 / 2N₀ t₀ (η₀² - 2η₀⁴)(10⁴ / ρ″)¹ = 75,3584967

Se efectueaza transformarea coordonatelor rectangulare stereografice din planul tangent (x_tg; y_tg), in planul secant unic - 1970, prin inmultirea coordonatelor x_tg si y_tg cu coeficientul de reducere la scara C = 0,999750000:

X_sec = x_tg C si y_sec = y_tg C Se exprima coordonatele rectangulare plane x_<70> si y_<70> in sistemul oficial STEREO - 70 cu originea translata, pe baza relatiilor:

x_<70> = x₀ + x_sec

y_<70> = y₀ + y_sec

unde: x₀ = 500000,000m si y₀ = 500000,000m.

Coordonatele rectangulare plane STEREO - 70 se exprima cu trei zecimale.

Transformarea coordonatelor geografice in coordonate plane STEREO - 70 , pe baza formulelor cu coeficienti constanti, se face cu o precizie de determinare de ±0,01 m.

Aplicarea formulelor de transformare a coordonatelor geografice in coordonate plane STEREO - 70 se poate face atat pentru colturile trapezelor geodezice, cat si pentru diferite puncte izolate de pe suprafata elipsoidului de referinta KRASOVSKI - 1940.

Rezolvarea practica a formulelor cu coeficienti constanti se poate face in cadrul tabelelor tipizate, unde sunt inscrise valorile numerice ale coeficientilor constanti, precum si cu ajutorul unui program de calcul tabelar.

3.2. Calculul coordonatelor rectangulare plane STEREO - 70 ale colturilor trapezului cu nomenclatura L-35-32-C-a-4-IV din coordonatele geografice

In baza formulelor 3.12 cu coeficienti constanti, care in cazul teritoriului Romaniei au fost calculati pentru centrul de proiectie Q₀ (φ₀ = 46s si λ ₀ = 25s ); in elipsoidul de referinta Krasovski, se efectueaza transformarea coordonatelor geografice (φ, λ) in coordonate rectangulare plane STEREO -70 (φ, λ).

Pentru exemplificare, se considera coordonatele geografice (φ, λ) pentru 4 puncte ce formeaza cadrul unui trapez la scara 1:5 000.(1 NW, 2 NE, 3 SV si 4 SE)

Transformarea se efectueaza intr-un formular tipizat unde sunt inscrise valorile numerice ale coeficientilor constanti si in care se inregistreaza: coordonatele geografice, numarul punctului, nomenclatura si scara trapezului.

Operatiile de transformare a coordonatelor (φ, λ) in coordonate STEREO (x, y) se efectueaza mai intai pe planul tangent (x_tg, y_tg) si apoi pe planul secant (x_<70>, y_<70>), in urmatoarea succesiune:

Se calculeaza mai intai pentru punctul 1 NW diferentele ∆φs =(φs_P - φs₀) = 1s 06′ 15″ si ∆ λ s =( λs_P - λ ^s₀) = 2s 35′ 37,5″ , care se transforma in secunde si apoi se scriu sub forma:

f = ∆φ″10^-4 = 0,397500

l = ∆ λ″ 10^-4 = 0,933750.

Se efectueaza produsele din formulele definite anterior intre coeficientii constanti din coloanele 2, 3, 4, 5 cu termenii din coloana 1, obtinandu-se:

S₀ = (a₀₀ + a₁₀ * f + a₂₀ * f² + a₃₀ * f³ + a₄₀ * f⁴ + a₅₀ * f⁵ + a₆₀ * f⁶) = 122747,374620297

S₂ = (a₀₂ + a₁₂ * f + a₂₂ * f² + a₃₂ * f³ + a₄₂ * f⁴) = 3711,3650789

S₄ = (a₀₄ + a₁₄ * f + a₂₄ * f²) = 0,311212517

S₆ = (a₀₆) = - 0,0000575

S₁ = (b₀₁ + b₁₁ * f + b₂₁ * f² + b₃₁ * f³ + b₄₁ * f⁴ + b₅₁ * f⁵) = 210878,7423874

S₃ = (b₀₃ + b₁₃ * f + b₂₃ * f² + b₃₃) = -23,9593437

S5 = (b₀₅ + b₁₅ * f) = -0,008448

Se efectueaza produsele dintre sumele S₀, S₂, S₄, S₆ si termenii 1, 1², 1⁴, 1⁶ si respectiv, dintre S₁, S₃, S₅ si 1, 1³, 1⁵ pe baza carora se obtin rezultatele partiale r₀, r₂, r₄, r₆ si r₁, r₃, r₅, ce se inscriu in coloana R:

r₀ = S₀ 1,000 = 122747,3746203;

r₂ = S₂ 1² = 3235,8987583;    r₁ =S₁ 1 = 196908,0257042

r₄ = S₄ 1⁴ = 0,2365808; r₃ =S₄ 1³ = -19,5059342

r₆ = S₆ 1⁶ = -0,0000381; _{<70> <70>} r₅ =S₅ 1⁵ = - 0,0059966

Se insumeaza algebric rezultatele partiale (r) din coloana R si se exprima coordonatele din planul tangent de proiectie stereografica - 1970

X_tg = r₀ + r₂ + r₄ + r₆ = 125983,510 m Y_tg = r₁ + r₃ + r₅ = 196888,514m

Prin inmultirea coordonatelor x_tg, y_tg cu coeficientul de reducere la scara, rezulta coordonatele din planul secant:

x _sec = x_tg * C = 125952,014 m    y _sec = y_tg * C = 196839,292 m

Se efectueaza translarea coordonatelor rectangulare plane din planul secant (x _sec, y _sec) in sistemul oficial STEREO - 70, cu originea translata, in baza relatiilor:

x _<70> =x _sec + 500000,000 m = 625952,014 m y _<70> = y _sec + 500000,000 m = 696839,292 m

In mod asemanator se calculeaza si pentru celelalte trei puncte.

Capitolul 4. Cadrul si dimensiunile trapezelor pe suprafata elipsoidului de referinta Krasovski 1940

4.1. Calculul laturilor si diagonalei trapezului L-35-32-C-a-4-IV pe suprafata elipsoidului de referinta Krasovski 1940

Hartile si planurile topografice in proiectia STEREOGRAFICA-1970 au un cadru geografic, ce rezulta din imaginile plane ale unor arce de meridiane si de paralele, care pe elipsoidul de referinta delimiteaza trapeze curbilinii, denumite si trapeze geodezice sau in mod curent trapeze, iar in planul de proiectie porta denumirea de foi de harta sau foi de plan.

Lungimile arcelor de meridian (s_m ) si de paralel (s_pN, s_ps) se determina in functie de diferenta de latitudine (∆φ) dintre arcele de paralel care delimiteaza un trapez, la o scara standard, la nord (φ_N) si la sud (φ_S) si respectiv, de longitudine (∆ λ) dintre arcele de meridian care delimiteaza un trapez de la est (λ_E) si la vest (λ_W), pe baza relatiilor:

◘ s_m = M_m (φ_N-φ_S)"/ ρ" =a(1-e²)(φ_N-φ_S)"/ρ"√(1-e²sin²φ_m )³ [m]

in care: M_m-raza medie de curbura a elipsei meridiane;

φ_m= (φ_N-φ_S)"/2-latitudinea medie a trapezului

◘ s_pN=r_N(λ_E-λ_W)"/ ρ"=acosφ_N(λ_E-λ_W)"/ ρ" √(1-e²sin²φ_N ) [m]

in care:r-raza de curbura a paralelului de latitudine (φ_N);

◘ s_pS=r_N(λ_E-λ_W)"/ ρ"=acosφ_s(λ_E-λ_W)"/ ρ" √(1-e²sin²φ_S ) [m]

in care:r-raza de curbura a paralelului de latitudine (φ_S);

Deoarece meridianele si paralele formeaza pe suprafata elipsoidului de referinta, o retea curbilinie rectangulara (i=90), se poate calcula lungimea diagonalei trapezului (sd), in cazul unui triunghi infinitezimal considerat plan, cu ajutorul unei formule care exprima media geometrica:

s_d²=s_m²+s_pN*s_pS sau s_d= √(s_m²+s_pN*s_pS) [m]

4.2. Calculul ariei trapezului L-35-32-C-a-4-IV pe suprafata elipsoidului de referinta Krasowski-1940

Aria trapezului(T) de pe elipsoidul Krasovski, delimitat de doua meridiane de longitudine λ_E si λ_W si de doua paralele de latitudine φ_N si φ_S, se determina in functie de coordonatele geografice respective, cu ajutorul formulelor cu coeficienti constanti:

◘ T=[ ∆T(φ_N) _∆λ=1' - ∆T(φ_S) _∆λ=1' ]( λ_E - λ_W )' [km²] sau [ha]

in care: ∆T(φ_N) _∆λ=1' si ∆T(φ_S) _∆λ=1' sunt elemente de arie elipsoidala;

( λ_E - λ_W )'- diferenta de longitudine, exprimata in minute si parti de minute;

4.3. Cadrul si dimensiunile trapezelor in planul secant al proiectiei stereografice-1970

Dimensiunile trapezelor din planul secant al proiectiei stereografice-1970 reprezinta imaginile plane ale lungimilor corespunzatoare de pe suprafata elipsoidului de referintǎ, care se determinǎ fie din coordonatele plane STEREO-70(X<70>;Y<70>), fie prin aplicarea unei corectii de reducere la planul STEREO-70 a elementelor elipsoidale, in functie de marimea modulului de deformare liniarǎ (μ) si areolarǎ (p=μ²).

In cazul folosirii coordonatelor rectangulare plane STEREO-70 se aplicǎ urmatoarele formule:

b=b₃₁=√∆x²₃₁+∆y²₃₁ [m] sau b=b₄₂=√∆x²₄₂+∆y²₄₂ [m]

a_N=a_N12=√∆x²₁₂+∆y²₁₂ [m] si a_S=a_S34=√∆x²₃₄+∆y²₃₄ [m]

d=d₃₂=√b²+a_Na_S [m]

±2S= Σ x _i(y _i+1-y _i-1) = - Σ y _i(x _i+1-x _i-1) [ha] cu i = 1śn

Pe baza elementelor dimensionale si a coordonatelor plane stereografice-1970 ale colturilor trapezelor, se raporteaza si se verifica cadrul interior al originalului foilor de plan sau de harta . Totodata, se intocmeste schema cu dimensiunile trapezului in cm. (laturile, diagonala )si aria trapezului(S) in ha, ce se deseneaza ca element cartografic in afara cadrului, in partea stanga si de sud a foii de plan.

5. Cadrul si dimensiunile trapezelor pe planul secant al proiectiei stereografice-1970

5.1.Calculul laturilor si diagonalelor trapezului L-35-32-C-a-4-IV in planul secant al proiectiei stereo-70

Dimensiunile trapezelor din planul secant al proiectiei stereografice-1970 reprezinta imaginile plane ale lungimilor corespunzatoare de pe suprafata elipsoidului de referinta, care se determina fie din coordonatele plane stereografice (X<70>; Y<70>), fie prin aplicarea unei corectii de reducere la planul STEREO-70 a elementelor elipsoidale, in functie de marimea modulului de deformatie liniara (μ) si areolara (p=μ² ).

Deoarece in proiectia Stereo-70 care este o proiectie conforma se deformeaza lungimile si suprafetele se cere ca sa fie determinate si dimensiunile si ariile trapezelor in functie de coordonatele plane rectangulare stereo-70.

Din punct de vedere principial dimensiunile si aria trapezului considerat pe suprafata elipsoidului de referinta se poate exprima in mod direct functie de coordonatele geografice elipsoidale, iar indirect prin calculul care consta din aplicarea unei corectii de reducere la plan.

In functie de coordonatele rectangulare stereo-70 ale colturilor trapezului considerat la scara 1:5 000, se calculeaza mai intai dimensiunile laturilor si ale diagonalei, precum si a suprafetei prin metoda numerica - procedeul analitic.

r₀ = 201,718 [km]

Se considera coordonatele rectangulare plane stereo-70 ale colturilor trapezului cu nomenclatura L-35-32-C-a-4-IV la scara 1:5 000 (fig. 5.1).

Operatiile de calcul ale lungimii laturilor si al diagonalei trapezului considerat in functie de coordonatele plane stereo-70 se efectueaza in succesiunea de mai jos, iar rezultatele se vor inscrie in tabelul 5.3.

5.1.1. Calculul lungimii laturilor neparalele (b)

Pentru calculul celor doua laturi neparalele b=13 si b=24 ale trapezului considerat in planul secant al proiectiei stereo-70,se folosesc relatiile de urmatoarea forma:

b = 13 = d₁₃ = √(x₃ - x₁)² + (y₃ - y₁)² = √(Δx₁₃² + Δy₁₃ ²) [m]

b = 24 = d₂₄ = √(x₄ - x₂)² + (y₄ - y₂)² = √(Δx₂₄² + Δy₂₄²) [m]

5.1.2. Calculul lungimilor laturilor paralele (a_N si a_S)

Lungimile laturilor paralele a_N si a_S ale trapezului considerat se determina asemanator pe baza formulelor de mai jos, iar rezultatele se trec in tabel:

a_N = 12 = d₁₂ = √(x₂ - x₁)² + (y₂ - y₁)² = √ (Δx₁₂² + Δy₁₂²) [m]

a_S = 34 = d34 =√(x₄ - x₃)² + (y₄ -y₃)² = √Δx342 + Δy₃₄²) [m]

5.1.3. Calculul diagonalei trapezului (d)

Diagonala trapezului se exprima fie din coordonatele plane ale punctelor 2 si 3, iar mai riguros ca medie geometrica a laturilor paralele si neparalele cu relatiile de mai jos:

d = 32 = d₃₂ = √[(x₂ - x₃)² + (y₂ - y₃)²] = √(Δx₃₂² + Δy₃₂²) [m]

d = 41 = d₄₁ = √[(x₄ - x₁)² + (y₄ - y₁)²] = √(Δx₄₁² + Δy₄₁²) [m]

d = 32 = √(b² + a_N*a_S)

5.2. Calculul ariei trapezului din planul proiectiei stereografice-1970

Pentru calculul ariei trapezului considerat din planul proiectiei stereo-70 se foloseste metoda analitica si procedeul analitic ce utilizeaza coordonatele rectangulare ale colturilor trapezului si relatiile de urmatoarea forma generala:

2S = Σ x_i (y_i+1 - y_i-1) [m²] [ha]

-2S = Σ yi (x_i+1 - x_i-1) [m²] [ha] i = 1, 2, 3, 4

Calculul propriu-zis se efectueaza in tabelul 5.4. unde conform schemei de calcul se va respecta sensul direct de parcurgere si notare a punctelor de pe conturul trapezului in succesiunea 1-2-4-3 cu repetarea punctului 3 la inceput si 1 la sfarsit adica 3 1 2 4 3 1.

Controlul modului de calcul al suprafetei trapezului considerat la scara 1:5 000 se face prin cele doua relatii 2S si -2S, prin rezultatul obtinut care trebuie sa fie identic, adica +2S = -2S.

Suprafetele se exprima mai intai in m² , iar apoi in hectare.

2S = x₁(y₂ - y₃) + x₂(y₄ - y₁) + x₄(y₃ - y₂) + x₃(y₁ - y₄)

-2S = y₁(x₂ - x₃) + y₂(x₄ - x₁) + y₄(x₃ - x₂) + y₃(x₁ - x₄)

5.3. Intocmirea inventarului cu elementele dimensionale si aria trapezului de pe elipsoidul de referinta si din planul stereo-70

Pe baza elementelor calculate atat pe suprafata elipsoidului de referinta Krasovski cat si din planul proiectiei stereo-70 se intocmeste inventarul cu datele obtinute in cazul trapezului considerat la scara 1:5 000.

In inventarul elementelor dimensionale se vor inscrie valorile numerice obtinute in "m" pentru lungime si in "ha" pentru suprafete.

Valorile metrice ale lungimilor laturilor si diagonalei calculate din coordonatele din planul de proiectie stereo-70 se transforma in valori centimetrice prin inmultirea cu un coeficient 100* s₀ unde s₀ =1/N =1/5000.

Deci dimensiunile laturilor si diagonalei trapezului in cazul scarii 1:5 000 se vor transforma prin inmultirea valorii metrice cu coeficientul 100*1/5000 = 0.02.

b [cm] =b [m] *0,02

a_N[cm] =a_N[m] *0,02

a_S[cm] =a_S[m] *0,02

d[cm] =d[m] *0,02

Pe baza acestor elemente se raporteaza si se verifica cadrul interior al trapezului pe scara 1:5 000.

Schita trapezului cu dimensiuni in "cm" din planul proiectiei stereo-70 si aria trapezului nedeformata de pe elipsoidul Krasovski se deseneaza sub latura de sud in afara cadrului ornamental al foii de plan.

6. Calculul deformatiilor in proiectia stereografica - 1970

Prin adoptarea proiectiei - 1970, care fiind o proiectie conforma pastreaza unghiurile dar deformeaza lungimile si suprafetele, s-a avut in vedre compensarea deformarilor negative cu cele pozitive prin adoptarea planului secant paralel cu cel tangent. In figura 6.1 se prezinta cercul deformatiilor nule R₀ = 201,718 km

6.1. Deformatiile lungimilor in proiectia stereografica-1970

In cazul planului secant unic al proiectiei sterografice-1970, s-a urmarit satisfacerea conditiei ca deformarile lungimilor din punctul central al proiectiei Q₀(φ₀,λ₀) sa fie aproximativ egale cu cele de la hotarele teritoriului Romaniei , adica:

Δr_centru =Δr_hotar =Δr_maxim /2

Pentru cele trei distante analizate cu lungimea de 275 km, 300 km si 380 km,intre centrul proiectiei si punctele marginale ale teritoriului Romaniei, s-a ajuns la concluzia ca pentru planul secant-1970 sa se adopte coeficientul de reducere la scara cu valoarea:

C = 1 - 1/4000 = 0,999 750 000

Deci in baza relatiei de mai sus, deformatia liniara relativa (D₀) denumita si deformatia regionala (Δr) din centrul de proiectie Q₀(φ₀,λ₀), este egala cu:

D0 =Δr = - 1/4000 = - 0.000 250 km/km = - 0,250 m/km

a)Deformatia liniara relativa, pe unitatea de lungime (1 km), din planul tangent al proiectiei stereografice-1970

● Deformatia liniara relativa( D_tg) dintr-un punct oarecare al planului tangent la sfera in punctul Q₀(φ₀, λ₀), poate fi calculata cu ajutorul formulei:

D_tg = L²/4R₀² [km/km] sau [m/km]

in care: L- distanta masurata pe sfera, intre polul proiectiei Q₀ si punctul considerat,in general, reprezinta mijlocul unei linii geodezice sau a unui trapez geodezic

R₀=6378,956681 km-raza medie de curbura la latitudinea φ₀ = 46s

b)Deformatia liniara relativa, pe unitatea de lungime (1km), din planul secant al proiectiei stero-1970

● Deformatia liniara relativa (D_sec) dintr-un punct oarecare al planului secant unic-1970, se determina cu relatia:

D_sec =D0 + L²/4R₀² +L⁴/24R₀² [km/km]

In relatia anterioara se introduce D0 = - 0,000 250 km/km si rezulta:

D_sec = - 0,000250 km/km + L²/4R₀² +L⁴/24R₀² [km/km]

Se neglijeaza termenul in L⁴ din relatia de mai sus, care este mai mic decat 10^-6 si se scrie: D_sec = - 0,000250 km/km + L²/4R₀² [km/km]

In relatia precedenta se inlocuieste distanta (L) de pe sfera cu lungimea corespunzatoare din planul de proiectie secant (ρ), care se determina in functie de coordonatele STEREO-70 ale punctului dat (x, y) si ale punctului (X0=0,000m; Y0=0,000m).

Deci, se considera: L = ρ = √(∆x² +∆y²) =√[(x-x₀)² +(y-y₀)²]

sau L ≈ ρ² = (∆x² +∆y²) [km] sau [m]

Deformatiile liniare relative calculate cu relatiile de mai sus se exprima in km/km dupa care se determina in m/km sau cm/km.

c)Modulul de deformatie liniara (μ)

Modulul de deformatie liniara μ se poate obtine cu relatia:

μ = 1+D_sec = 1+L²/4R₀² - 0,000250

6.2. Deformatiile suprafetelor in proiectie STEREO-70

Deformatiile suprafetelor au aceleasi semne si aceeasi variatie cu cele ale lungimilor, fiind negative in interiorul cercului de secanta si pozitive in afara cercului de secanta, iar valoarea modulului de deformatie areolara, se obtine cu relatia:

p =μ²

Pentru exemplificare a modului de calcul a deformatiei suprafetelor, se considera aria trapezului de pe elipsoidul de referinta (T) si din planul proiectiei (S), precum si coordonatele rectangulare plane (X<70>;Y<70>) ale punctului M pe baza carora se calculeaza:

• Deformatia liniara relativa (D _km/km), din punctul M: D_secM =-0,000250+(∆x²_Q0M+∆y²_Q0M)/4R₀²
• Modulul de deformatie liniara (μ), din punctul M: μ_M=1+ D_secM
• Modulul de deformatie areolara (p), din punctul M: p_M= μ_M²
• Deformatia areolara relativa (P), din punctul M: P=(p-1)
• Deformatia areolara totala ( ∆T): ∆T=P*T_elipsoid

Pentru verificarea modului de calcul a deformatiei areolare se poate exprima marimea deformatiei areolare totale (∆T) si in functie de diferenta dintre cele doua suprafete calculate pe elipsoid si in planul STEREO-70: ∆Ts=(S_ha-T_ha).

Aria trapezului din planul de proiectie calculata din coordonatele plane trebuie sa fie egala cu cea obtinuta cu relatia: S_ha=p*T_ha

6.3 Calculul deformatiilor lungimilor in trapezul cu nomenclatura L-35-32-C-a-4-IV la scara 1:5 000 in functie de coordonatele rectangulare plane STEREO-70

In cadrul teritoriului cadastral al comunei Barnpva din judetul Iasi se cere sa se determine marimea deformatiilor liniare din mijlocul laturilor paralele ale trapezului cu nomenclatura L-35-32-C-a-4-IV la scara 1:5 000.

Pentru calculul deformatiilor liniare (D) si a modulului de deformatie liniara (μ) din mijlocul laturilor paralele aN si aS ale trapezului considerat la scara 1:5 000 se considera cunoscute coordonatele STEREO-70 ale colturilor 1,2,3,4 ale trapezului dat. In functie de aceste coordonate se determina media aritmetica a coordonatelor punctelor din mijlocul laturilor 12 si 34 adica MN si Ms cu relatiile :

X_MN = (x₁+x₂)/2 Y_MN = (y₁+y₂)/2

asemanator X_MS = (x₃+x₄)/2 si Y_MS =(y₃+y₄)/2.

Valorile acestor coordonate se exprima cu trei zecimale si se inscriu in tabelul 6.1.

Pe baza acestor coordonate se exprima deformatiile liniare dupa cum urmeaza:

a)      Calculul deformatiei liniare relative (D) din plan secant unic de proiectie STEREO-70, exprimata cu relatia din capitolul anterior

b)      Calculul modulului de deformatie liniara (μ) se calculeaza ca si la 6.2 dar se face pentru μ_MN si pentru μ_MS in [km/km]

c)      Calculul deformatiei totale a lungimii laturilor trapezului(∆_T)

Deformatia totala a lungimii laturilor de pe elipsoid care se reprezinta in planul proiectiei STEREO-70 se exprima functie de lungimea liniei geodezice considerate si de marimea deformatiei liniare relative in km/km din punctul de mijloc al liniei considerate. Se folosesc relatiile de calcul de forma :

∆_T =s*D_sec [m]; ∆_{T MN}=s_PN[km]*D_sec[km/km]; ∆_{T MS}=s_PS[km]*D_sec[km/km], rezultatele se inscriu in tabelul6.1

6.4 Calculul deformatiilor lungimilor in trapezul L-35-32-C-a-4-IV, functie de laturile trapezului de pe elipsoid si din planul STEREO-70

Pentru calculul deformatiilor liniare dintr-un trapez al ridicarii in plan se rezolva si problema inversa si anume pornindu-se de la lungimile cunoscute ale laturilor trapezului dat (s_PN si s_PS) si (a_N, a_S) se verifica din punct de vedere practic calculul efectuat anterior si se inscriu rezultatele in tabelul 6.1.

In functie de lungimile laturilor trapezului considerat se exprima mai intai deformatia totala cu ajutorul expresiilor ∆T_N=a_N - s_PN [m],∆T_S=a_S - s_PS [m] si se inscriu in tabelul 6.1.Cele doua valori ale deformatiilor totale obtinute prin cele doua metode trebuie sa fie egale, iar in baza relatiilor de mai sus s_PN*D_MN=a_N-s_PN si s_PS*D_MS=a_S - s_PS

Se observa ca din cele doua relatii rezulta D_MN si D_MS, iar rezultatele se inscriu in coloana deformatiilor liniare mai intai in [km/km] si apoi in [m/km].

Din punct de vedere practic valorile deformatiilor liniare relative calculate in functie de coordonatele STEREO-70 si functie de lungimile laturilor trapezelor de pe elipsoid si plan trebuie sa fie egale.

Se exprima modulul de deformatie μ=S/s pe baza raportului general de forma μ=S(plan)/s(elipsoid).Relatia se aplica pentru μ_MN si μ_MS .

6.5Calculul deformatiei suprafetelor in trapezul cu nomenclatura L-35-32-C-a-4-IV in functie de coordonatele plane STEREO-70

In proiectia stereo-70 deformatiile areolare au aceleasi semne ± cu cele ale deformatiilor liniare fiind negative in interiorul cercului de deformatie nula si pozitive in exteriorul sau. Pe baza coordonatelor STEREO-70 ale colturilor trapezului dat care mai intai se inscriu in tabelul 6.2 se determina coordonatele punctelor din mijlocul trapezului cu relatiile X_M=(x1+x2+x3+x4)/4 [m], Y_M=(y1+y2+y3+y4)/4 [m].

In continuare se exprima urmatoarele elemente:

Deformatia liniara D_km/km din punctul M mai intai in [km/km] si apoi in [m/km]

Modulul de deformatie liniara μ_M [km/km]

Modulul de deformatie areolara ce se obtine cu relatia P_M= μ_M²

Deformatia areolara relativa ( P_M) se calculeaza functie de modulul de deformatie areolara P_M = p_M -1

Deformatia areolara totala ∆Ts a suprafetei trapezului dat se obtine in functie de marimea deformatiei areolare (P) ce se inmulteste cu suprafata calculata pe elipsoid : ∆Ts = P_M * T _{elipsoid de referinta} [ha] si [m²] si se inscrie in tabel.

6.6 Calculul deformatiei suprafetei in trapezul L-35-32-C-a-4-IV in functie de ariile trapezului pe elipsoid si din planul proiectiei STEREO-70

Pentru verificarea modului de calcul, functie de coordonatele rectangulare plane se determina elementele p, P,∆Ts, si in functie de ariile cunoscute ale trapezului S si T se inscriu in tabelul 6.2 in [ha] si [m²].

Pe baza acestor arii se calculeaza urmatoarele elemente:

►modulul de deformatie areolara (p) sub forma raportului dintre suprafata trapezului din planul STEREO-70 pe suprafata omoloaga de pe elipsoid: p=S/T

► deformatia areolara totala ∆Ts =Sha - Tha in [ha]

► deformatia areolara relativa P ce se obtine in functie de marimea deformatiei totale ∆Ts si de suprafata trapezului de pe elipsoid P=∆Ts/T

Egalitatea valorilor obtinute atat pentru deformatii liniare cat si pentru cele areolare pana la ordinul 6 zecimal confirma corectitudinea modului de calcul al lungimilor si suprafetelor

Intocmirea si redactare originalelor de teren ale hartilor si planurilor

Pe baza masuratorilor destinate intocmirii de noi planuri topo-cadastrale sau de actualizare a celor existente si a calculelor necesare pentru determinarea coordonatelor retelelor de sprijin si a celor de detaliu, se trece la intocmirea originalelor de teren ale foilor de plan, iar prin generalizare a foilor hartii.

7.1 Metode de intocmire a planurilor topografice

In functie de modul de executare a masuratorilor se disting urmatoarele metode:

a.       intocmirea originalelor de teren pe baza masuratorilor topografice clasice;

b.      intocmirea originalelor de teren pe baza datelor culese cu statiile totale;

c.       intocmirea originalelor de teren pe cale fotogrammetrica, pe baza lucrarilor de reperaj si descriere topografica a fotogramelor aeriene.

Reprezentarea grafica in cadrul interior al originalelor de teren a foilor hartii sau planurilor care delimiteaza un trapez geodezic de latitudine si longitudine, rezulta in urma raportarii coordonatelor rectangulare ale celor 4 colturi ale trapezelor la scarile 1: 50000, 1: 25000, 1: 10000, 1: 2000, 1: 1000 si 1: 500. In cazul foilor de harta intocmite la scari mai mici sau egale cu 1: 100000, pe langa cele 4 colturi se mai considera si un punct de frantura pe latura de nord si de sud a trapezului.

In procesul clasic de intocmire si editare a originalelor de tern s-au folosit intr-o prima etapa suporturi nedeformabile realizate din hartie alba de desen de calitate superioara, lipita pe placi de aluminiu sau de zinc. Intr-o a doua etapa, s-a trecut la utilizarea suporturilor nedeformabile din materiale plastice sub forma de placi si foi netransparente sau transparente.

Raportarea coordonatelor rectangulare plane (X, Y) ale colturilor trapezelor corespunzatoare foilor de harta si de plan precum si ale retelei topografice de sprijin si de ridicare, s-a realizat in sistem clasic cu ajutorul coordonatelor rectangulare de tip mare din seria ZEISS. Aceste coordonatografe asigura raportarea coordonatelor rectangulare pe suporturi ale originalelor de teren cu suprafete utile maxime, de la 80 * 80 si pana la 90 * 120 cm, in limitele unei precizii de raportare grafica de la ± 0,1mm pana la ± 0,05 mm la scara de reprezentare

In procesul automatizat de intocmire si editare a planurilor topografice se realizeaza culegerea, prelucrarea, reprezentarea grafica si folosirea datelor topografice cadastrale sub forma digitala. Din punct de vedere practic, datele topografice cadastrale necesare la intocmirea hartilor si planurilor topografice se realizeaza in sistem automatizat, in functie de provenienta lor: date ale receptoarelor GPS, date ale statiilor totale de masurare , date fotogrammetrice si date digitizate dupa harti si planuri existente.

Raportarea cadrului interior al originalului de teren

Coordonatele colturilor trapezelor corespunzatoare foilor de harta si de plan se raporteaza pe baza urmatoarelor operatii pregatitoare si de raportare grafica:

a.       Pregatirea suportului originalului de teren, functie de dimensiunile grafice ale plansei foii de harta sau de plan;

b.      Intocmirea inventarului de coordonate rectangulare plane si de coordonate grafice de raportare ale colturilor trapezului

Pe baza coordonatelor rectangulare plane (X<70>, Y<70>) ale celor patru colturi ale unui trapez (1, 2, 3, 4) se stabilesc mai intai coordonatele punctului C₀ (X₀, Y₀) considerat origine ajutatoare de raportare, in functie de scara de reprezentare (tabelul 7.1)   

Tabelul 7.1 Inventarul de coordonate rectangulare plane si grafice de raportare ale colturilor unui trapez, la scara 1: 50000 si la scara 1:5000.

Pe baza celor doua conditii X₀ < Xmin si Y₀ < Ymin si a unei rotunjiri de pana la 1000 . 1500 m, se vor obtine coordonatele punctului origine C₀ (X₀, Y₀), care pe formatul de desen se amplaseaza in apropierea coltului de sud - vest al trapezului care se raporteaza.

Calculul coordonatelor grafice de raportare (X′, Y′) la scara 1:5000 se efectueaza cu ajutorul relatiilor:

X′_i = 100 s₀ (X_i - X₀) (cm) si Y′_i = 100s₀ (Y_i - Y₀) (cm)

unde: i = 1, 2, 3, 4 - colturile trapezului

s₀ = 1 / N - scara de reprezentarea originalului de teren

(X_i, Y_i) - coordonatele rectangulare plane STEREO - 70

(X₀, Y₀) - coordonatele rectangulare plane STEREO - 70 ale originii ajutatoare de raportare.

In cazul scarii de reprezentare 1: 5000, se folosesc relatiile:

X′_i = 0,02 (X_i - X₀) (cm)

Y′_i = 0,02 (Y_i - Y₀) (cm)

S = 549,6287 ha

47,47 cm

66,32 cm

47,45 cm

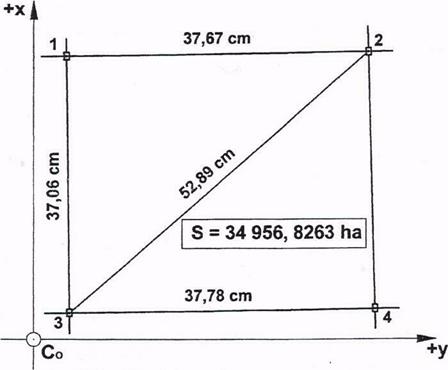
Fig. 7.1 - Cadrul interior cu dimensiunile si aria unui trapez la scara 1 : 5 000

c.       Raportarea coordonatelor rectangulare ale colturilor trapezului

Raportarea coordonatelor grafice (X′₁, Y′₁) ale colturilor trapezului (tabelul 7.1), ce s-au calculat in raport cu originea ajutatoare C₀ (X₀, Y₀), se efectueaza astfel:

se stabileste pozitia originii ajutatoare in coltul din stanga jos a plansei printr-o intepatura fina cu diametrul de 0,1 mm, care se marcheaza in creion, printr-un cerculet cu diametrul de 2mm, iar in partea dreapta se va scrie denumirea punctului.

se raporteaza cele 4 colturi ale trapezului conform inventarului grafic de coordonate cu precizia de ± 0,2 mm la scara de reprezentare, care se evidentiaza mai intai printr-o intepatura foarte fina cu diametrul de 0,1 mm in creion, apoi intr-un patrat de 2mm langa care se va scrie numarul punctului (fig. 7.1)

d.      Verificarea si definitivarea raportarii cadrului interior

Dupa raportarea celor 4 colturi ale cadrului interior, se trece la verificarea modului de raportare, care se face prin masurarea laturilor si a diagonalei trapezului (a_N, a_s, b, d) cu ajutorul riglelor de precizie si a compasului cu tija.

Precizia grafica a originalelor de teren raportate la scara 1: 5000 se verifica in limita erorii maxime admise la raportarea punctului prin coordonate rectangulare, care pentru colturile trapezelor este de ± 0,2 mm la scara de reprezentare. Pentru control, se compara elementele grafice masurate cu originalul de teren cu dimensiunile laturilor s ia diagonalei trapezului calculate in cm, in limita erorii de ± 0,2 mm.

Dupa verificarea raportarii, se traseaza in creion cadrul interior prin unirea celor 4 colturi cu linii drepte subtiri de grosime 0,1 mm, care se prelungesc cu cate 10 mm in afara cadrului interior, in vederea construirii cadrului geografic si a cadrului ornamental.

Trasarea cadrului geografic si ornamental al originalului de teren

Cadrul geografic se traseaza la o distanta de 7 mm de cadrul interior al hartii si respectiv la 8 mm de cel al planului, prin prelungirea acestuia in sens orizontal si vertical, printr-o linie dubla cu latimea de 1 mm si grosimea de 0,1 mm.

Pe lungimea grafica a cadrului geografic, care este egala cu cea a cadrului interior, se marcheaza prin segmente de dreapta innegrite alternativ valorile grafice din minut in minut pe latitudine si longitudine ale laturilor foilor de harta si de plan. Linia dubla a cadrului geografic se innegreste alternativ pe o grosime de 0,5 mm sau 1 mm, incepand din coltul de sud - vest in sensul de deasupra si spre dreapta pentru valorile pare ale latitudinii si ale longitudinii. In cazul valorilor impare ale latitudinii si longitudinii se traseaza mai intai segmentele albe si apoi cele innegrite.

In functie de caracterul hartii sau planului, se marcheaza prin puncte amplasate in spatiul cuprins dintre cadrul geografic si cadrul ornamental, reteaua geografica divizata in secunde pe lungimea grafica corespunzatoare unui minut de latitudine sau de longitudine:

din 20" in 20", pentru scara 1:50000;

din 10" in 10", pentru scara 1:25000;

din 10" in 10", pentru scara 1:10000;

din 5" in 5", pentru scara 1:50000;

Pentru exemplificare, se prezinta modul de trasare a cadrului geografic pe intervale de 1 minut si subintervale de 20" in cazul unei foi de harta la scara 1:50000 cu ∆φ = 10'00" si ∆λ = 15'00", in functie de urmatoarele coordonate geografice ale punctului de sud - vest al trapezului:

φ_SV = 47˚20'00" ; λ_SV = 26˚15'00"

Pe mijlocul celor 4 laturi ale cadrului geografic se va lasa un spatiu liber, unde se va scrie nomenclatura trapezelor vecine care sa fie citita in sensul normal (de la stanga la dreapta) si respectiv de jos in sus. In continuare se traseaza la o distanta de 9 mm de cadrul interior si la o distanta de 1 mm de cadrul geografic, un alt de punct 1 mm grosime, care formeaza cadrul ornamental al foii de harta sau de plan( Fig. 8.1 ).

Trasarea retelei rectangulare a originalului de teren

In functie de scara de intocmire a originalului de teren se traseaza si o retea rectangulara sau kilometrica in spatiul dintre cadrul interior si cadrul geografic sau pe intreaga suprafata a unei foi de harta sau plan.

Densitatea retelei rectangulare este cuprinsa intre valori ce se traseaza din 200 in 200 m pe scara 1: 2000 si din 10 in 10 km in cazul scarii 1: 500000 (tabelul 9.1).

Densitatea retelei rectangulare sau kilometrice pe originalul de teren al foilor de plan si de harta

Tabel 9.1

Pe foile de plan intocmite la scara 1: 2000, 1: 5000 si 1:10000 se traseaza reteaua rectangulara cu densitatea prezentata in tabelul 9.1 numai pe spatiul cuprins intre cadrul interior si cadrul geografic unde se vor inscrie valorile numerice conform valorii scarii de raportare

Pentru scara de raportare 1: 5000, reteaua rectangulara se traseaza din 0,5 in 0,5 km sau 500 in 500 m adica cu latura pe planul de 10 cm.

Se considera trapezul cu nomenclatura L-35-32-C-a-4-IV la scara 1: 5000 pe care se vor trasa mai intai cele patru drepte de baza X = X_N, X = X_S, Y = Y_V, Y = Y_E si apoi paralele intre ele la 10 cm , functie de inventarul de coordonate plane din figura 7.1.

Pentru trasarea dreptei X = X_N (1, 2) se traseaza arcele de cerc de raza l₁ = X₁ - X_N cu centrul in punctul 1 si raza r₂ = X₂ - X_N cu centrul in punctul 2 ce se calculeaza in cm pe baza relatiilor de mai jos:

X_N < X₁ ; X_N < X₂ r₁ = 0,02 * X_N

Pentru trasarea dreptei X = X_S se procedeaza asemanator stabilindu-se valorile X_S > X₃ , X_S >X₄, razele r₃ si r₄ se obtin cu relatiile:

r₃ = 0,02 * (X_S - X₃) (cm)    r₄ = 0,02 * (X_S - X₄) (cm)

Spatiul de pe cele 2 verticale din stanga si dreapta se imparte din 10 in 10 cm riguros si rezulta punctele pe care se traseaza reteaua rectangulara orizontala.

Valorile retelei se scriu in spatiul dintre cadrul interior si geografic cu 1 zecimala. In continuare se traseaza reteaua rectangulara verticala din punctul 13 si 24. Pentru trasarea dreptei Y =Y_W ce trece pe langa 1 si 3 se stabilesc valorile Y_W > Y₁, Y_W > Y₃, iar pe baza lor se calculeaza razele r₅ cu centrul in punctul 1 si r₀ cu centrul in punctul 6.

Pentru trasarea Y = Y_E se stabilesc valorile Y_E < Y₂, Y_E < Y₄ se calculeaza r₇ si r₈.

Raportarea punctelor de baza ale retelelor de triangulatie si nivelment din interiorul cadrului originalului de teren la scara 1: 5 000

Dupa raportarea cadrului originalului de teren si retelei kilometrice sau rectangulare din 10in 10 cm se trece la raportarea punctelor de baza ce au fost determinate cu precizie atat planimetric cat si altimetric pe suprafata terestra apoi pe suprafata elipsoidului sau geoidului.

Reteaua geodezica de baza a ridicarilor topo de detaliu de pe suprafata ce formeaza obiectul ridicarilor este calculata din urmatoarele categorii de puncte oricare ar fi reteaua geodezica de ordin superior I, II, III, IV in proiectia STEREO - 70 si plan de referinta altimetrica Marea Neagra.

Tab.10.1.Coordonatele rectangulare ale punctelor retelei de sprijin

- determinarea planimetrica a acestor puncte se face prin coordonatele geografice si coordonatele geografice / rectangulare;

- coordonatele rectangulare plane ale acestor puncte provin din transformarea coordonatelor plane determinate in proiectia Gauss - Kruger prin formule cu coeficienti constanti ce asigura o transformare de ± 1 cm realizat pe intregul teritoriul Romaniei.

Oricare ar fi reteaua geodezica de indesire ce cuprinde punctele de ordin V ce s-au determinat pe baza retelei de triangulatie de ordin superior si care impreuna cu reteaua I - IV formeaza reteaua de sprijin a tuturor retelelor la orice scara.

La reteaua de indesire se includ urmatoarele puncte:

punctele geodezice determinate in alte sisteme de proiectie prin transcalculare in proiectia STEREO - 70;

punctele retelelor locale ce se pot calcula prin transcalculare in proiectia STEREO - 70;

punctele retelelor poligonometrice ce au fost determinate pe baza retelelor determinate mai sus si cele determinate prin metoda trilateratiei;

reperele si marcile nivelmentului de strat I - V si a nivelmentul geometric executat pentru diferite lucrari tehnice.

Precizia de raportare a punctului de baza trebuie sa fie maxima si corespunzatoare planului ce se redacteaza. Reprezentarea acestor puncte se va face in conformitate cu atlasul de semne conventionale pentru planurile topo 1: 2000, 1: 5000, 1: 10000 din care se prezinta:

punct astronomic

punct de triangulatie geodezica

Raportarea punctului de pe conturul unui imobil sau corp de proprietate din interiorul cadrului originalului de teren la scara 1: 5 000

Incadrarea punctului de amplasament si delimitare al unui corp de proprietate in cadrul trapezului la scara 1: 5000 se va realiza prin raportarea punctelor de pe conturul imobilului pe baza inventarierii de coordonate din sistemul de proiectie STEREO - 70.

Tabelul 11.1

Inventarul de coordonate STEREO - 70 ale punctelor de pe conturul corpului de proprietate

Reprezentarea elementelor de continut ale planului topo - cadastral la scara 1: 5 000

Elementele de planimetrie se reprezinta pe planuri topografice la scarile 1: 2000, 1: 5000 si 1: 10000 potrivit formei si dimensiunilor ce le au in teren fie la scara respectiva daca acest lucru este posibil fie prin semne conventionale.

a. Elemente topografice in interiorul localitatilor

Pe planurile oraselor se reprezinta reteaua stradala conform sistemelor din teren:

strazile cu latimea mai mica de 5 m la scara 1: 5000 si 1: 10000 se reprezinta cu doua linii cu 0,5 mm intre ele;

- strazile cu latimea mai mare de5 m la scara 1: 5000 si 1: 10000 se reprezinta la scara planului;

spatiile verzi - in interiorul contururilor se aplica semnul conventional sau simbolul categoriei de folosinta corespunzatoare cu situatia din teren;

se delimiteaza prin linii de grosime 0,1 mm;

constructii industriale, agricole si social culturale se reprezinta pe plan, prin semne conventionale ale imprejmuirilor si elemente componente pastrandu-se pozitia, dimensiunea si orientarea lor. In interiorul localitatilor se ridica urmatoarele elemente hidro: paraie, rauri, canale, vaduri, poduri, castele de apa, maluri consolidate.

b. Instalatii

Din categoria instalatiilor se vor ridica: statii meteo, cosurile fabricilor si uzinelor, transformatoare electrice, relee de televiziune, statii de alimentare auto, silozuri, cariere, centrale electrice si hidroelectrice, sere, etc.

c. Conducte, retele, imprejmuiri si limite

Conductele si retelele se reprezinta pe planul 1: 5000 si 1: 10000 in exteriorul localitatilor, pe teren se vor ridica : ziduri de beton, piatra, caramida; grajduri metalice, din lemn, vii, diguri artificiale de pamant.

Pe planul 1: 2000, 1: 5000, 1: 10000 se reprezinta limite de stat, judete, municipii, orase si comune.

d. Retele de comunicatii

reteaua de cai ferate si constructii auxiliare se ridica cu indicarea caracterului constructiei necesare reprezentate pe plan din care fac parte:

cai ferate normale, electrificate, in constructie sau demontate;

ramblee, deblee si ziduri de sprijin;

tuneluri, statii de cai ferate, depouri.

reteaua de drumuri - in vederea reprezentarii pe plan topo la scara 1: 5000, 1: 2000 si 1: 10000 - autostrazi, sosele, drumuri imbunatatite, drumuri navale, poteci, alei in poarta si gradini;

e. Hidrografie si constructii hidrotehnice

Pentru reprezentarea hidrografiei si constructiilor hidrotehnice pe planul topo la scara 1: 2000, 1: 5000 si 1: 10000 se vor ridica pe teren urmatoarele detalii:

izvoare si fantani;

apele curgatoare (inclusiv canalele);

iazuri, balti, lacuri si marile;

diguri si baraje;

podurile, trecerile si vadurile;

instalatii de deservire a navigatiei;

posturile hidrometrice;

Apele cu latimea mai mica de 3 m se ridica pe axul longitudinal cu specificarea latimii. Apele cu latimea mai mare de 3 m se ridica pe ambele maluri. Se indica sensul de curgere printr-o sageata.

Dintre constructiile hidrotehnice ce se reprezinta pe plan topo 1: 2000, 1: 5000, 1: 10000 se vor ridica pe teren baraje de beton, lemn, pamant, ecluzele, castele de apa, apeducte, podurile, vadurile, etc.

e. Categoriile de folosinta ale terenului - se reprezinta pe plan topo la scarile 1: 2000, 1: 5000, 1: 10000 prin limitele respective cand suprafata lor depaseste 20 mm².

se reprezinta prin simboluri din atlasul de semne conventionale: arabil (A), pasuni (P), fanete (F), vii (V), livezi (L), paduri si alte terenuri cu regenerare forestiera (PD), hidrografie (H), neproductiv(N), drumuri si cai ferate (D), constructii si alte terenuri (C).

f. Inscriptii explicative

In scopul reprezentarii pe plan a detaliilor topo trebuie culese o serie de elemente suplimentare α - numerice pentru explicarea tipului sau caracteristicilor obiectelor ce vor fi reprezentate pe plan:

inaltimea terenului;

latimea terenului;

denumire a localitatilor, apelor, muntilor, dealurilor, etc.

a.      Culegerea pe teren a elementelor de toponimii

Planul topo la scarile 1: 2000, 1: 5000, 1: 10000, trebuie sa contina toate denumirile localitatilor, apelor, formelor de relief, padurilor. Deosebit de nomenclatura fiecare foaie de plan are o denumire stabilita functie de cel mai important detaliu cu denumirea topica ce-l contine.

13. Cartografierea originalelor de teren si planului topo - cadastral de baza la scara 1: 5 000

A.      Desenarea elementelor cadrului originalului de teren cadrul planului topo ce limiteaza reprezentarea grafica a suprafetei trapezului considerat cuprinde o serie de date grafice si numerice fiind format din urmatoarele parti:

Cadrul interior, se obtine prin raportarea coordonatelor rectangulare plane (X, Y) cu ajutorul coordonatografului sau in sistem automatizat, a colturilor trapezului corespunzator foii de harta sau de plan.

Cadrul geografic reprezinta dimensiunile grafice ale trapezului pe latitudine si pe longitudine, fiind format din imaginile plane ale arcelor de paralele si de meridiane, care delimiteaza in planul proiectiei cartografice suprafata unui trapez.

Cadrul ornamental sau exterior, se traseaza cu o linie continua de 1 mm grosime, la o distanta de 1 mm de cadrul geografic si de 9 mm de cadrul interior.

B.     Elemente si inscriptii ale originalelor de teren

Reteaua rectangulara (kilometrica) - se traseaza cu linii de 0,1 mm in spatiul dintre cadrul interior si cel ornamental, pentru planul 1: 5000 se traseaza din 10 in 10 cm.

Coordonatele geografice (φ, λ) ale celor 4 colturi se scriu in grade, minute, secunde si parti de secunde in punctul respectiv al foii de plan.

Valorile numerice ale retelei kilometrice se scriu in spatiul dintre cadrul interior si cadrul geografic di 0,5 in 0,5 km pentru scara 1: 5000.

Inscriptiile dintre cadrul interior si cel geografic se refera la urmatoarele elemente:

denumirea tarilor de pe o parte si alta a frontierelor;

denumirea localitatilor, judetelor, si a cadrului interior;

denumirea localitatilor reprezentate pe mai multe foi de plan insotite de prepozitia "de" in cazul cand denumirea respectiva nu este inscrisa pe plansa foii de plan, daca nu reprezinta titlul hartii sau planului;

denumirea localitatii ce indica directia spre care merg caile de comunicatii si distanta in kilometri pana la localitatea indicata;

Nomenclatorul foii de plan vecine se inscrie pe mijlocul ce formeaza cadrul geografic.

C.      Desene si inscriptii din afara cadrului

In afara cadrului ornamental se deseneaza o serie de elemente si se inscriu date grafice si numerice dupa cum urmeaza:

Inscriptii in afara cadrului pe latura de N:

proiectia stereografica - 1970;

sistem de cote Marea Neagra;

Romania, judetul Iasi.

Nomenclatura planului topografic.

Cadrul planului.

Caracterul planului:

Secret;

Nesecret;

Secret de serviciu;

Plan cadastral;

Desene si inscriptii sub latura de indicata.

Schema limitelor administrative si denumirea teritorial cadastrala cuprinse pe foaia de plan.

  1 - comuna Barnova

Schema si dimensiunile trapezului (latimea si diagonale in centimetri cu 2 zecimale), suprafata in hectare (4 zecimale) (de pe elipsoid).

Scara numerica cu mentiunea corespunzatoare unui centimetru de pe plan cu lungimea din teren in metri 1 cm plan = 50 m teren.

Scara grafica simpla corespunzatoare scarii numerice.

Indicatii redactionale se refera la date cu privire la intocmirea planurilor, originalelor de autori, editare, anul editarii, numele institutiei executante.

14.Verificarea lucrarilor de intocmire si redactare a originalelor de teren la scara 1: 5000

Verificarea originalelor de teren se executa pe grupe de elemente dupa cum urmeaza:

a.       La elementele de cadru si nomenclatura se vor verifica:

dimensiunile cadrului si suprafata trapezului;

trasarea si aplicarea valorilor retelei kilometrice;

trasarea si aplicarea valorilor cadrului geografic;

nomenclatura planului, scara si specificatiile referitoare la impartirea administrativa (scara grafica, 10 m harta =1 m teren, 1 comuna;

b.      La elementele de planimetrie se vor verifica:

felul, forma si dimensiunile punctului retelei de sprijin:

traseul si structura semnalelor de reprezentare a limitelor administrative;

conturul constructiilor inscriptiilor explicative in legatura cu acestea si reteaua de strazi din localitati;

caile de comunicatie si directiile lor;

reteaua hidrografica (latimile raurilor, confluenta, sensuri de scurgere);

uniformitatea grosimii si compactitatii tuturor liniilor;

respectarea structurii tuturor semnelor conventionale.

c.       Cu privire la scriere se vor verifica:

culegerea (cartografierea) corecta si completa a tuturor desenelor si inscriptiilor interioare si exterioare ale originalului;

folosirea corecta a caracteristicilor si corpurilor de litere stabilite in instructiuni si atlase;

amplasarea judicioasa si estetica a scrierii.

d.      Cu privire la racordari se vor verifica:

efectuarea racordarii pe cele 4 laturi ale trapezului pe toate elementele de planimetrie si hidrografie;

acolo unde in cazul transmiterii racordarii de la un trapez la altul apar abateri mai mari de 0,5 mm pentru elementele principale ale planului (cai de comunicatie, ape, etc.) si 1 mm pentru celelalte elemente (contur de proprietate, etc.) se vor lua masuri pentru remedierea abaterilor constatate.

Tabelul 4.1.

Calculul lungimii laturilor si a diagonalelor trapezelor de pe suprafata elipsoidului Krasovski in functie de coordonatele geografice(φ,λ)

Intocmit: ing. Popa Georgel

Verificat:Prof. univ. dr. ing. Valeriu Moca