Tabele de dispersie

Tabele de dispersie

Ne punem problema mentinerii unui set finit de date, fiecare dintre ele identificata printr-o cheie unica, si notam cu K multimea cheilor din acest set, numita multimea cheilor actuale. Prin natura lor, fie ca sunt intregi de lungime fixa, dar mare, fie ca sunt stringuri de caractere, cheile actuale K fac parte dintr-o multime U, de cardinalitate mult mai mare decat K, numita universul cheilor, lucru pe care il notam |K|<<|U|. Pe aceasta multime dorim sa facem operatii de inserare si stergere, si, de asemenea, foarte frecvent, operatii de cautare. Ideal ar fi ca operatia de cautare sa aiba timp O(1) sau apropiat de el, in orice caz timp constant (si mic) in raport cu cheile din U. Structura de date care ne permite accesul in timp O(1) la orice componenta este vectorul. Daca ne-am putea permite mentinerea in memorie a unui vector T a carui multime de indici sa fie chiar U, atunci pentru orice cheie actuala k Є K, in locatia T[k] am putea mentine data identificata de cheia k. Un asemenea T se numeste tabel cu adresare directa. Din pacate, pentru multe probleme concrete nu ne putem permite aceasta solutie deoarece ar conduce la o risipa de spatiu. Dam mai jos cateva exemple.

1.Vrem sa mentinem inregistrari cu date despre cei 68 de angajati ai unei firme. Fiecare angajat este identificat cu ajutorul unui numar de cod compus din 4 cifre. Cardinalul multimii cheilor actuale este |K|=68, dar universul cheilor U este format din multimea tuturor intregilor cu 4 cifre in scriere zecimala, deci |U|=10⁴=10000. Un tabel cu adresare directa ar insemna sa mentinem in memorie un vector cu 10000 de componente, dintre care doar 68 ar fi efectiv folosite.

2. Vrem sa mentinem inregistrari cu date despre populatia Romaniei. Fiecare locuitor este identificat cu ajutorul unor chei unice, codul numeric personal, un intreg compus din 12 cifre. Cardinalul multimii cheilor actuale este aproximativ 22 de milioane, |K|=22*10⁶. Universul cheilor va fi multimea tuturor intregilor de 12 cifre, deci va avea dimensiunea |U|=10¹².

3.Anuarul telefonic al unei localitati mentine informatii despre abonatii identificati cu ajutorul numelui si prenumelui, deci un sir de maximum 20 de caractere deci va avea dimensiunea |U|=26²°.

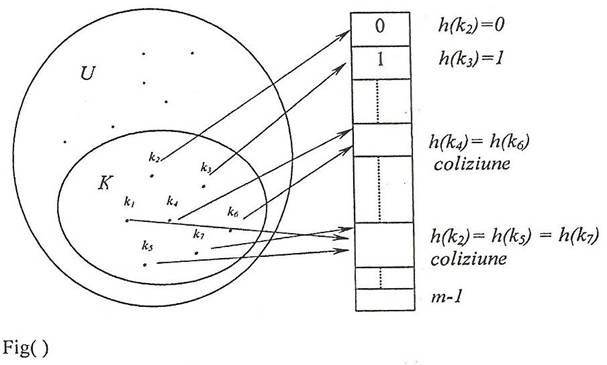
In toate situatiile descrise mai sus este nerealista folosirea unui tabel cu adresare directa, adica a unui tabel T indexat chiar dupa U. Trebuie sa gasim o multime de indici pentru T, de cardinal m, mult mai mic decat |U|, eventual apropiat de cardinalul lui K, si o metoda de a dispersa cheile din K pe multimea de indici . Cu alte cuvinte, avem nevoie de o functie, definita pe universul cheilor si cu valori in multimea indicilor T.

h:U→

cu ajutorul careia sa gasim locul fiecarei date din multimea noastra: data identificata printr-o cheie k, k Є K, sa se afle in locatia T[h(k)] a tabelului T.

O asemenea functie se numeste functie de dispersie. Pentru a fi o functie buna de dispersie, functia h trebuie sa indeplineasca anumite cerinte, si anume:

1. Sa se poata calcula rapid. Timpul de calcul al lui h(k) ne va da timpul de acces la componenta T[h(k)].

2. Codomeniul ei sa fie cat mai mic. Este dezirabil ca m sa fie cat mai apropiat de |K|, in orice caz diferenta dintre ele sa fie acceptabila ca dimensiune.

3. h sa fie cat mai aproape de o functie surjectiva, adica sa avem cat mai putine locatii goale. Aceasta cerinta se leaga de precedenta.

4. h sa fie cat mai aproape de o functie injectiva pe K. Cu alte cuvinte, pentru chei k₁, k₂ Є K, k₁≠k₂ sa avem h(k₁)≠h(k₂).

Numim coliziune a cheilor k₁ si k₂ situatia in care h(k₁)=h(k₂). Cerinta 4 se exprima si sub forma "ne dorim sa avem cat mai putine coliziuni". Din pacate coliziunile nu pot fi evitate complet si trebuie gasite metode de rezolvare a lor.

Pentru a folosi un tabel de dispersie programatorul trebuie sa rezolve doua probleme: sa aleaga o functie de dispersie si sa opteze pentru o metoda de rezolvare a coliziunilor. Aceasta din urma se imparte in doua mari clase : rezolvarea coliziunilor prin inlantuire(cand locatia T[h(k)] contine o lista inlantuita a tuturor inregistrarilor cu chei ce au colizionat cu k ) si rezolvarea coliziunilor prin adresare directa, cand se folosesc metode mai sofisticate de cautare a unei locatii libere in T pentru o cheie care colizioneaza.

Ne vom ocupa pe rand de cele 2 tipuri de probleme.

Functii de dispersie

Ne ocupam in acest paragraf de prezentarea catorva tehnici euristice de creare a unor functii de dispersie bune. Am exprimat informal in paragraful precedent cateva cerinte pentru o asemenea functie h:U→.

Vom lucra la ipoteza hashingului simplu uniform ( HSU ), care , informal, spune ca orice cheie este distribuita prin functia h cu probabilitate egala in oricare din locatiile . Mai precis, pentru oricare hЄK probabilitatea ca h(k)=i este 1/m pentru orice iЄ[0..m-1], si este independenta de restul cheilor.

Daca P este probabilitatea de distrubutie a cheilor din K in U, adica daca P(k)=probabilitatea de a extrage cheia k din U, atunci ipoteza HSU se formuleaza:

pentru orice i = 0,1,.,m-1

Deoarece P este de obicei necunoscuta , nu este in general posibil sa verificam ca ipoteza HSU este satisfacuta .

In cele ce urmeaza vom interpreta cheile si numerele naturale, adica vom considera ca U<N. Atunci cand cheile sunt stringuri, metoda folosita pentru a le converti la numere naturale este urmatoarea: se inlocuieste fiecare caracter cu codul sau ASCII si se calculeaza valoarea sirului rezultat ca intreg in baza 128.

De exemplu :

AB se scrie 65

ABC se scrie 65 66 =65*128² + 66 * 128 +67 = 1073605

Metoda diviziuni

Se numesc functii de dispersie obtinute prin metoda diviziunii functiile de forma

h:U→, h(k) = k mod m.

Ele sunt printre cele mai comune pentru ca sunt usor de calculat.

Alegerea unei astfel de functii revine practic la alegerea lui m, dimensiunea tabelului de dispersie. Deci , ea va fi guvernata, pe de o parte , de dimensiunile lui K si de modul in care rezolvam coliziunile. De exemplu, daca ne propunem sa le rezolvam prin inlantuire si sa mentinem in medie 3 date intr-o locatie, m ar putea fi apropiat de |K|/3. Daca insa vrem ca toate elementele din K sa-si gaseasca locul in tabel, atunci am putea alege un m apropiat de 3|K|/2 , acceptand deci o risipa de spatiu egala cu |K|/2.

Dar acestea nu sunt singurele considerente care guverneaza alegerea lui m. Important este ca cheile sa fie bine dispersate pe multimea si sa avem cat mai putine coliziuni. Vom evita valori pentru m de forma lui 2, deoarece , daca m=2 atunci h(k) = k mod reprezinta doar ultimii p biti din scrierea binara a lui k. Am pierdut in felul acesta informatia continuta in ceilalti biti, lucru nerecomandabil: daca nu avem indicatii contrare, trebuie sa facem ca h(k) sa depinda de toti bitii lui ?. Numerele apropiate de puteri ale lui 2 sunt si ele de evitat .Un exemplu de rezultat care ne conduce la aceasta decizie este urmatorul: daca m= si cheile k sunt siruri de caractere in baza , atunci 2 siruri care difera doar printr-o transpozitie a doua caractere adiacente vor avea aceeasi valoare prin h.

Vom evita si valori pentru m de forma puterilor lui 10 , caci daca am alege un asemenea m, atunci h(k) nu ar ? decat de o parte a caracterelor ce apar in scrierea lui k in baza 10. Valori bune pentru aceasta metoda sunt m, un numar prim si cat mai departe de puteri ale lui 2. Evident , ne putem propune sa indexam tabelul dupa multimea de indici , in caz in care functiile din aceasta clasa vor fi de forma h(k) = k mod m+1.

Sa consideram exemplul firmei cu 68 de angajati, identificati cu chei intregi cu 4 cifre in scrierea in baza 10. Sa presupunem ca alegem pentru tabel o dimensiune apropiata de 3|K|/2= 3/2*68. O buna alegere pentru m ar fi m=97, deoarece este prim , apropiat de 3/2*68 si destul de departe de puteri ale lui 2.

Sa consideram cheile k₁ = 3205, k₂=7148 si k₃=2345.

Cu functia de dispersie data de metoda diviziunii

h(k)=k mod 97

Obtinem pentru aceste chei urmatoarele adrese din tabel :

h(k₁) = 3205 mod 97 = 4

h(k₂) = 7148 mod 97 = 67

h(k₃) = 2345 mod 97 = 17

Metoda multiplicarii

Fie A o constanta pozitiva subunitara ,0<A<1.

Sa consideram functia data de

h(k) = |_ m ( kA mod 1)_|

kA mod 1 reprezinta partea fractionara a lui kA, kA - [kA], care se inmulteste cu m, iar rezultatul se trunchiaza la cel mai apropiat intreg.

Observam ca valoarea lui m nu e critica pentru aceasta metoda, iar puterile lui 2 sunt alegeri bune pentru m, pentru ca functia se va calcula usor. Fie m=. Atunci

h(k) =|_ (kA-[kA])_| = |_kA [kA]_|

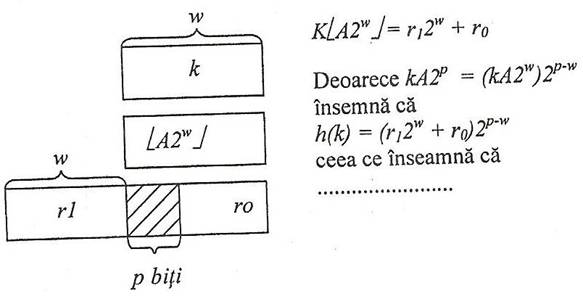
Fie w lungimea unui cuvant masina in biti si presupunem ca k se poate reprezenta pe w biti de forma

Knuth recomanda pentru A numarul de aur, , a carui valoare aproximata cu 7 zecimale este 0,6180339.

Revenind la exemplul nostru, sa alegem pentru aceasta metoda A=0,6180339 si m=2⁶=64. Atunci, pentru cele 3 chei din exemplu si functia h(k)=|_m(kA mod 1)_|, avem:

h(k₁)=h(3205)=51

deoarece partea fractionala a lui 3205, A este 0,7986, care, inmultit cu 64 ne da 51,1107, a carui parte intreaga este 51.

Analog, obtinem

h(k₂)=h(7148)=45 si h(k₃)=h(2345)=18

Metoda impachetarii

Metoda impachetarii sau folding genereaza functii de dispersie in felul urmator. Fiecare cheie k, despre care am facut presupunerea ca este intreg, este partitionata in bucati de lungimi egale (eventual cu exceptia ultimei), k₁, k₂,,. Daca k este un intreg scris in baza 10 bucatile vor fi siruri de caractere in baza 10, de aceeasi lungime fixa, l, pe care din nou le putem considera intregi. O functie de dispersie

h:U→[0 10²-1] este data de formula

h(k)=(k₁+k₂++)mod

ceea ce inseamna ca se aduna cele r bucati, ca intregi, si din suma se pastreaza doar l cifre, cele mai putin semnificative. Alte functii de dispersie se obtin inversand ordinea cifrelor in toate bucatile pare sau in toate bucatile impare. De exemplu:

h(k)=(+k₂++) mod

unde k este intregul obtinut prin inversarea ordinii caracterelor.

Pe exemplul nostru metoda impachetarii se aplica in felul urmator: spargem fiecare cheie de 4 caractere in 2 bucati de cate 2 caractere, pe care le adunam si omitem, daca e cazul, cifra cea mai nesemnificativa pentru ca rezultatul sa aiba lungimea tot de 2 caractere. Avem deci

h(k₁)=h(3205)=32+5=37

h(k₂)=h(7148)=(71+48)mod 100=19

h(k₃)=h(2345)=23+45=68

Pentru functia h'(k)=k₁+ in care a doua functie o inversam in oglinda inainte de adunare, obtinem

h'(3205)=32+

h'(7148)=71+=(71+84)mod 100= 55

h'(2345)=23+

Metoda patratului

Presupunem ca l este lungimea fixata a lui h(k) ca intreg in baza 10. Fie h:U→[0], h(k)=(k² div ) mod

Se ridica la patrat, iar din intregul lung astfel obtinut se elimina cifre dintre cele mai putin semnificative si cifre dintre cele mai semnificative, pastrandu-se exact l cifre din 'centrul' lui k². Cu alte cuvinte si l sunt fixate, iar se obtine din formula l = lung(k²)-

Sa aplicam aceasta metoda exemplului nostru. O cheie de 4 cifre va avea patratul de 7 sau 8 cifre, dintre care sa eliminam =3 dintre cele din dreapta, sa pastram l=2 cifre, si sa eliminam si restul de cifre 'centrale', adica a 4-a si a 5-a din stanga.

k₁=3205 : k₁²=3205²=102025 si h(k₁)=72

k₂=7148 : k₂²=7148²=510904 si h(k₂)=93

k₃=2345 : k₃²=2345²=54025 si h(k₃)=99