 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
ing. mecanica
Modelare, simulare in dinamica sistemelor mecanice II
Se da :
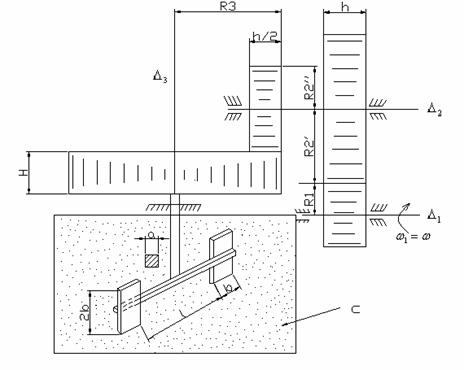
Sistemul mecanic din figura transmite
miscarea de la un motor la un rotor montat pe axul ![]() si care se gaseste intr-o incinta cu un fluid.
Caracteristica mecanica
a motorului e liniara,
si care se gaseste intr-o incinta cu un fluid.
Caracteristica mecanica
a motorului e liniara, ![]() .Fluidul dezvolta
pe suprafata de atac a rotrului o presiune opusa miscarii, proportionala
cu viteza punctului de pe suprafata sa, coeficientul de proportionalitate fiind
.Fluidul dezvolta
pe suprafata de atac a rotrului o presiune opusa miscarii, proportionala
cu viteza punctului de pe suprafata sa, coeficientul de proportionalitate fiind
![]()
Se cere:
Sa se stabileasca ecuatia diferentiala a miscarii sistemului;
Sa se integreze analitic ecuatia
diferentiala a miscarii trasandu-se diagrama ![]() ;
;
Sa se integreze numeric ecuatia diferentiala prin metoda Runge-Kutta.
Miscarea relative a rotilor de transmitere a miscarii e o rostogolire fara alunecare.
![]()
|
Nr. |
|
|
|
|
|
|
|
|
|
|
|
rad/s |
|
1 |
60 |
140 |
60 |
300 |
20 |
100 |
200 |
40 |
60 |
15 |
30 |
80 |
Studiul cinematic:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
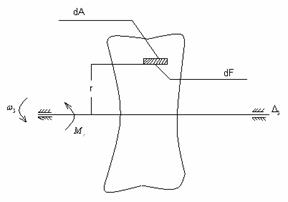
Evaluarea momentului rezistent la axul de iesire:
![]()
![]()
![]()
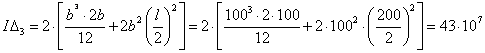
Studiul ecuatiei miscarii folosind teorema energiei cinetice:
![]()
![]()
![]()
![]()
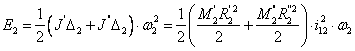
![]()
![]()
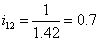
![]()
![]()
![]()
![]()
![]()
![]()
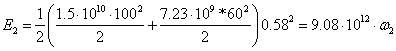
![]()
![]()
![]()
![]()
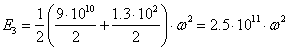
![]()
Sa se integreze analitic ecuatia diferentiala a miscarii trasandu-se
diagrama ![]()
![]() ;
; ![]() ;
; ![]()
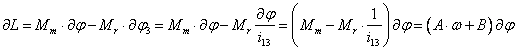
![]() momentul motor ;
momentul motor ;
![]() momentul rezistent .
momentul rezistent .
![]() ;
; ![]()
![]()
![]()
![]()
![]() ;
; ![]()
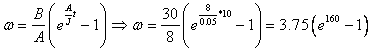
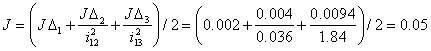
![]()
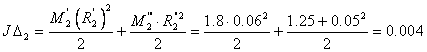
![]()
Graficul unghiului de pozitie
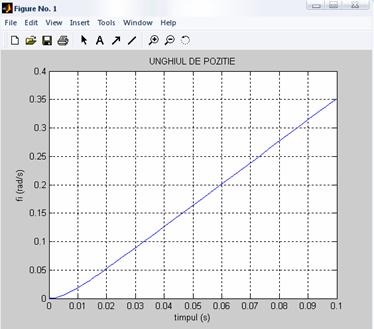
Graficul vitezei unghiulare
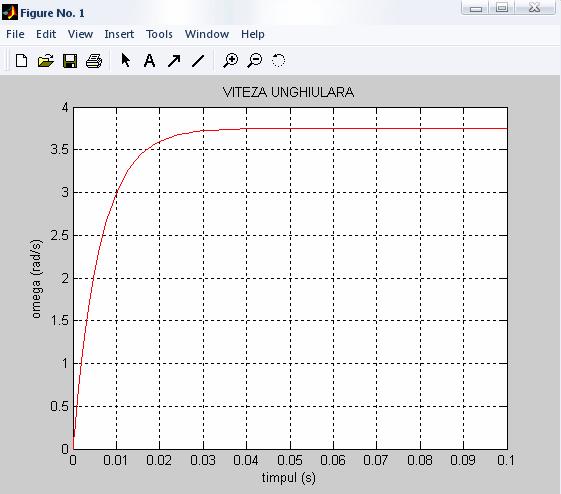
Copyright © 2026 - Toate drepturile rezervate