 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
PROBLEMELE REZISTENTEI MATERIALELOR
OBIECTUL SI PROBLEMELE "REZISTENTEI MATERIALELOR "
Rezistenta materialelor este o disciplina de cultura tehnica generala , care continua si dezvolta " Mecanica teoretica " prin introducerea in calcule a proprietatilor de deformabilitate ale solidelor . In " Mecanica teoretica " ,solidul rigid este considerat nedeformabil , actionat de forte , care sunt vectori alunecatori . "Rezistenta materialelor " studiaza solidul rigid real - pe care il numeste element de rezistenta , piesa sau simplu corp ,- actionat de forte ( ce se numesc incarcari si sunt vectori legati ( au punctul de aplicatie fix ) . Elementul de rezistenta , sub actiunea incarcarii , isi schimba forma geometrica si dimensiunile initiale , devenind deformabil , la anumite valori ale incarcarii , rupandu-se . Prin calculele de rezistenta se determina dimensiunile sectiunilor transversale ale corpului , in functie de marimea , pozitia , modul de actionare al fortelor exterioare , de proprietatile mecanice ale corpului , de importanta ansamblului din care face parte corpul ,prin coeficienti de siguranta , uneori tinand cont de durata de functionare a acestuia .
Elementele de rezistenta terbuie sa indeplineasca urmatoarele conditii de baza
Conditia de rezistenta
tensiunile
sa nu produca ruperea ![]()
Conditia de rigiditate
deformatia efectiva sa nu depaseasca deformatia admisa![]()
Conditia de stabilitate
elementul de rezistenta sa-si mentina forma de echilibru stabil pentru o anumita incarcare .
Problemele " Rezistentei materialelor " se rezolva pe baza urmatoarelor criterii :
criteriul economic
orice piesa proictata trebuie sa se realizeze cu solutia cea mai economica ;
criteriul de buna functionalitate
pe baza acestui criteriu ,intreg ansamblul din care face parte piesa proiectata trebuie sa aiba o buna functionare , aceasta , respectand ,conditiile de rezistenta , rigiditate si stabilitate .
" Rezistenta materialelor " permite rezolvarea urmatoarelor categorii de probleme :
Probleme de dimensionare
prin care se stabilesc dimensiunile optime si forma geometrica ale pieselor proiectate , in functie de incarcarea exterioara si caracteristicile mecanice ale materialului din care este confectionata piesa , din conditiile de rezistenta , rigiditate sau stabilitate cerute , respectand criteriile enuntate anterior .
2 .Probleme de verificare
prin care se
stabileste
daca
piesa , de dimensiuni cunoscute si
material dat , satisface conditia
de rezistenta
, rigiditate sau stabilitate ceruta
, cunoscand
incarcarea
exterioara
.![]()
![]()
3 .Probleme de calcul a incarcarii capabile
prin care , pentru un element de rezistenta , ale carui dimensiuni ,caracteristici mecanice ale materialului sau , respectiv modul de solicitare sunt cunoscute , se determina incarcarea capabila
In rezolvarea problemelor de " Rezistenta materialelor " se intalnesc urmatoarele aspecte :
- aspectul geometric - furnizeaza expresii de calcul pentru determinarea deformatiilor ce apar ca urmare a solicitarilor exterioare ale piesei ;
- aspectul static - prin care se determina fortele de legatura (reactiunile) elementului de rezistenta cu mediul exterior , fortele interioare ,iar in final intensitatea solicitarii ;
- aspectul fizic - stabileste legatura intre cele doua aspecte enuntate anterior . Aceasta legatura se stabileste prin incercari de laborator.
1 .2 LEGATURA " REZISTENTEI MATERIALELOR "
CU ALTE DISCIPLINE
a )In " Mecanica teoretica " doua forte care actioneaza pe acelasi suport in sensuri contrare , de module egale ( oricat de
mari )sunt in echilibru ( figura 1.1 ) ![]()
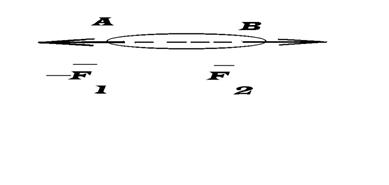
Fig 1 . 1
In "Rezistenta materialelor " acest echilibru exista , atata timp cat elementul de rezistenta ramane intreg. La valori mari ale fortelor , sunt depasite conditiile de rezistenta si rigiditate stabilite , elementul rupandu - se .
b ) In " Statica " forta " este considerata vector alunecator ,
iar momentul vector liber. In " Rezistenta
materialelor " atat
forta cat si momentul sunt vectori legati de punctul de aplicare . In figura l . l , forta ![]() actioneaza in punctul A iar
actioneaza in punctul A iar ![]() in punctul B ,
elementul de rezistenta fiind astfel intins . Daca se deplaseaza cele doua forte pe suportul lor astfel incat punctele de aplicatie sa se inverseze , respectiv ,
in punctul B ,
elementul de rezistenta fiind astfel intins . Daca se deplaseaza cele doua forte pe suportul lor astfel incat punctele de aplicatie sa se inverseze , respectiv , ![]() in B si
in B si ![]() in A ,echilibrul nu se modifica dar se schimba sensul de actiune al acestora , elementul devenind in
acest caz comprimat , deci solicitarea este diferita
in A ,echilibrul nu se modifica dar se schimba sensul de actiune al acestora , elementul devenind in
acest caz comprimat , deci solicitarea este diferita
c ) In " Mecanica teoretica " solidul rigid este considerat nedeformabil ( cu rigiditate infinita in ", " Mecanica fluidelor " corpurile au rigiditate nula ( de exemplu apa ) . In " Rezistenta materialelor " corpurile au rigiditate finita . Ele au o anumita elasticitasticitate .
CLASIFICAREA CORPURILOR IN REZISTENTA MATERIALELOR
In general , corpurile sau elementele de rezistenta au forme constructive complicate . In " Rezistenta materialelor " ele se schematizeaza , pentru simplificarea calculelor . In functie de raportul dintre dimensiunile geometrice principale ale acestora , se face urmatoarea clasificare :
barele - sunt elemente de rezistenta la care doua dimensiuni geometrice , comparabile intre ele sunt mult mai mici in comparatie cu a treia , numita lungime . Dupa forma sectiunii transversale exista bare de sectiune circulara , dreptunghiulara , patrata sau alte forme geometrice ( de exemplu profilele laminate )
Locul geometric al centrelor de greutate ale sectiunilor transversale se numeste axa geometrica a barei . Dupa forma geometrica a acestei axe , barele pot fi : drepte , curbe in plan sau in spatiu , cotite. Dupa modul de solicitare barele poarta diferite denumiri conventionale :
n tiranti - bare solicitate la intindere :
n stilpi - bare solicitate la compresiune :
n grinzi - bare solicitate la incovoiere ;
n arbori - bare solicitate la torsiune ( rasucire ) .
Daca , dimensiunea sectiunii transversale este foarte mica , bara avand rigiditate foarte mica neputand prelua solicitari de incovoiere , bara se numeste fir .
placile sunt elemente de rezistenta la care doua dimensiuni geometrice , comparabile intre ele , sunt mai mari in raport cu a treia , numita grosime .In interiorul placii (fig.1.2 ), la egala distanta de fetele acesteia , se gaseste suprafata mediana a placii .In functie de forma acestei suprafete mediane , se deosebesc : placi plane , curbe ( invelitori ) , vase , tuburi .
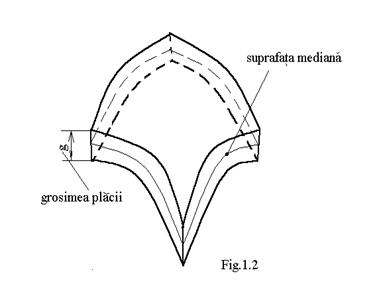
Daca grosimea placii este foarte mica , rigiditatea placii fiind de asemenea mica , placa se numeste membrana
masivele sunt elemente de rezistenta la care toate cele trei dimensiuni geometrice sunt comparabile intre ele ( au aproximativ acelasi ordin de marime - de exemplu : bilele sau rolele rulmentilor , batiul unei masini unelte , tuburile cu pereti grosi s.a. )
1 . 4 CLASIFICAREA INCARCARILOR EXTERIOARE
Elementele de rezistenta sunt supuse actiunii sarcinilor exterioare , care pot fi forte sau momente ( cupluri de forte ) , si care pot fi clasificate dupa diferite criterii :
Dupa modul de actiune al incarcarii :
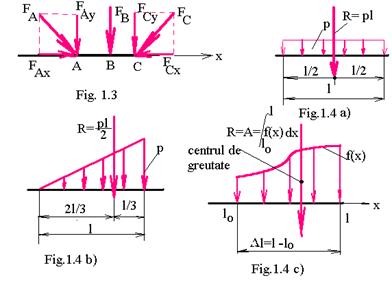
sarcini concentrate aplicate teoretic intr-un punct ( fig. 1 .
sarcini distribuite uniform ( fig . 1.4 a ) sau cu intensitati variabile in lungul axei barei ( fig . 1.4 b , c )
Conform principiului lui Saint -Venant ( principiu ce va fi enuntat ulterior ) aceste sarcini distribuite se inlocuiesc prin rezultanta ce actioneaza in centrul de greutate al suprafetei ce reprezinta modul de distributie al sarcinii respective , si de intensitate egala cu aria acestei suprafete ( fig . 1 .
Dupa modul de actionare in timp :
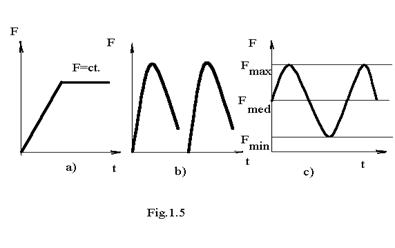
sarcini statice care se aplica lent si progresiv pana la valoarea maxima , apoi raman constante ( fig 1 . 3 ) pe tot parcursul actiunii ;
sarcini dinamice care se aplica cu viteze de incarcare relativ mari . Se deosebesc : sarcini aplicate prin soc cu variatie brusca de viteza ( fig 1 . 5 b ) sarcini variabile periodic intre o valoare maxima si una minima ( fig 1 . 5 c )
1 . 5 EFORTURI . SOLICITARI SIMPLE . SOLICITARI COMPUSE .
SEMNE CONVENTIONALE . CONVENTII DE SEMNE .
Pentru a determina eforturile in centrul sectiunii unui element de rezistenta , se utilizeaza metoda sectiunilor . Se sectioneaza elementul de rezistenta cu un plan imaginar , si se scriu ecuatiile de echilibru static pentru elementul din stanga planului de sectiune sau din dreapta . Elementele torsorului astfel obtinut , se proiecteaza pe axele sistemului de referinta si se obtin :
n componenta rezultantei dupa axa barei ( sau dupa o tangenta la axa barei in cazul barelor curbe ) se numeste forta axiala In mod conventional , aceasta se considera pozitiva cand intinde elementul de rezistenta si negativa cand il comprima
n componenta rezultantei continuta in planul sectiunii transversale se numaste forta taietoare In mod conventional , se considera forta taietoare pozitiva cand rasuceste elementul de rezistenta in sens orar, si negativa cand rasuceste in sens trigononetric .
n componenta momentului dupa axa barei se numeste moment de torsiune sau de rasucire In mod conventional , acesta are acelasi semn ca si forta axiala : pozitiv, cand iese din sectiune , negativ , cand intra in sectiune .
n componenta momentului continuta in planul sectiunii transversale , se numeste moment incovoietor In mod conventional , momentul incovoietor se considera pozitiv , cand intinde fibra inferioara si negativ cand intinde fibra superioara
Conventiile de semne ale tuturor eforturilor sunt exprimate sugestiv in figura 1.6.
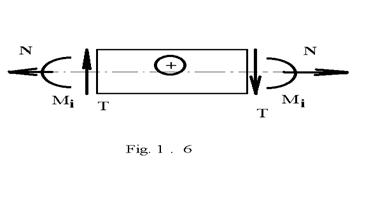 Daca sistemul de forte ce
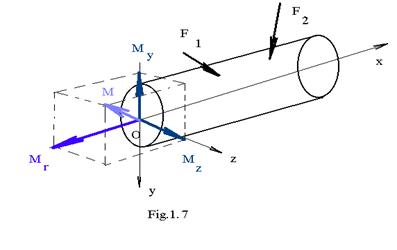
actioneaza asupra elementului de rezistenta este unul oarecare , nemai actionand intr-unul din planele principale de inertie
(xOy sau xOz ), momentul incovoietor va avea doua componente ( in planul sectiunii transversale ) una dirijata dupa Oz - Mz si una dirijara dupa Oy - My ( fig .1.
Daca sistemul de forte ce
actioneaza asupra elementului de rezistenta este unul oarecare , nemai actionand intr-unul din planele principale de inertie
(xOy sau xOz ), momentul incovoietor va avea doua componente ( in planul sectiunii transversale ) una dirijata dupa Oz - Mz si una dirijara dupa Oy - My ( fig .1.
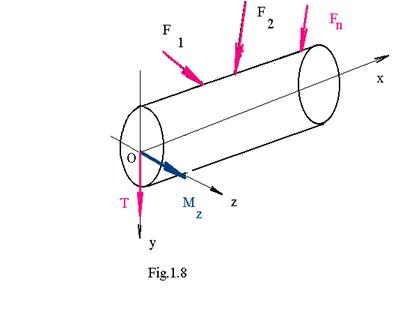
In cazul in care elementul de rezistenta este actionat de un sistem de forte coplanare ( de exemplu situat in planul xOy) momentul incovoietor este dirijat dupa axa perpendiculara pe planul fortelor , respectiv Oz , se noteaza Mz ( fig. 1.8 ) .
Marimile : N , T , M , Mt poarta numele de eforturi . Fiecare dintre ele , daca actioneaza asupra elementului de rezistenta singure , produc solicitari simple . Astfel :
n forta axiala N produce solicitarea de intindere sau compresiune ;
n forta taietoare T produce solicitarea de taiere sau forfecare ;
n momentul incovoietor ( dirijat dupa una din axele principale de inertie Mz sau My ) produce solicitarea de incovoiere - pura cand apare singur , sau simpla cand apare insotit de forta taietoare ;
n momentul de torsiune sau de rasucire Mt produce solicitarea de torsiune sau de rasucire .
Prezenta simultana a doua sau mai multe eforturi in centrul de greutate al sectiunii transversale , da nastere la solicitari compuse ( face exceptie momentul incovoietor insotit de forta taietoare in cazul incovoierii simple , care se considera solicitare simpla ).
1.6 TENSIUNI
( ASPECTUL STATIC AL PROBLEMELOR DE REZISTENTA MATERIALELOR )
Pentru a studia problemele rezistentei materialelor sub aspect static , s-a introdus notiunea de : tensiune , sau efort specific , sau efort unitar .( Sunt trei denumiri ce definesc aceeasi marime fizica
Tensiunea reprezinta intensitatea solicitarii unui sistem de forte inrt-un anumit punct al sectiunii transversale a elementului de rezistenta
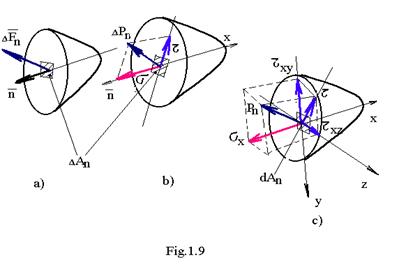
Se considera un element de rezistenta , din care , prin metode sectiunilor se seectioneaza cu un plan imaginar in locul in care se doreste determinarea tensiunilor . Se considera partea
din dreapta sectiunii de arie An , caracterizata de
vectorul normalei ![]() si al tangentei ( continute in planul sectiunii transversale )
si al tangentei ( continute in planul sectiunii transversale ) ![]() . Pe aceasta sectiune , se considera un element de arie A An pe care actioneaza forta interioara AFn , de directie oarecare ( diferita de cea a normalei )- figura 1.9 .
. Pe aceasta sectiune , se considera un element de arie A An pe care actioneaza forta interioara AFn , de directie oarecare ( diferita de cea a normalei )- figura 1.9 .
Valoarea raportului :
![]() ( 1 . 1 )
( 1 . 1 )
se numeste tensiune medie ( efort unitar mediu )
Trecand la limita se obtine :
![]() (
1 . 2 )
(
1 . 2 )
vectorul tensiune totala ( efort unitar total ). Unitatea de masura in sistem international este N/m2. O unitate de masura mult mai convenabila in practica este N/mm2 , sau mega pascalul ;
![]() ( 1 . 3 )
( 1 . 3 )
Tensiunea totala pn se poate descompune dupa normala la sectiune in tensiune normala sau efort unitar normal - cu efect de intindere sau compresiune a fibrelor elementului de rezistenta , si dupa tangenta la sectiune , in efort unitar tangential sau tensiune tangentiala - cu efect de taiere sau forfecare. Astfel intre aceste marimi se poate scrie relatia vectoriala :
![]() ( 1 . 4 )
( 1 . 4 )
sau scalar :
![]() ( 1 . 5 )
( 1 . 5 )
In cazul in
care se considera
un sistem cartezian cu originea in punctul considerat , astfel incat
, axa Ox sa
coincida
cu normala la sectiune
( ![]() ) ( figura 1.9-c ), se poate scrie :
) ( figura 1.9-c ), se poate scrie :
![]() ( 1 . 6 )
( 1 . 6 )
In jurul unui punct se pot duce o infinitate de suprafete elementare . Totalitatea tensiunilor care actioneaza in jurul unui punct al unui element de rezistenta reprezinta starea de tensiune din jurul acelui punct .
OBSERVATIE : Toate ecuatiile de echilibru static ( ecuatiile de echivalenta statica ) , de proiectii sau de momente se scriu cu forte ( eforturi ) nu cu tensiuni ( eforturi unitare ).
1.7 IPOTEZE DE BAZA IN REZISTENTA MATERIALELOR
Pentru a putea stabili formule de calcul in rezistenta materialelor , se introduc anumite ipoteze simplificatoare , ce permit dezvoltarea matematica a unor calcule si gasirea unor solutii relativ simple , cu o buna verificare in calculele practice.
O prima
simplificare s-a facut impart
a) Ipoteza mediului continuu si uniform ( ipoteza izotropiei )
In rezistenta materialelor se considera corpurile a fi continui , omogene , materialul ocupand tot volumul determinat de suprafata exterioara Proprietatile materialelor sunt aceleasi in toate directiile .
b) Ipoteza elasticitatii perfecte
In domeniul in care se stabilesc formulele din rezistenta materialelor se considera elementul de rezistenta confectionat din materiale perfect elastice , adica , dupa incetarea fortelor exterioare care il deformeaza , materialul revine la forma si dimensiunile initiale .
c) Ipoteza proportionalitatii dintre forta si deformatie
Se considera valabila legea lui Hooke , conform careia , deformatiile unui element de rezistenta se considera a fi proportionale cu fortele ce le produc .
d) Ipoteza micilor deformatii
conform careia , deformatiile elastice sunt mici in comparatie cu dimensiunile initiale ale pieselor astfel incat , la scrierea ecuatiilor de chilibru static , ele se neglijeaza .
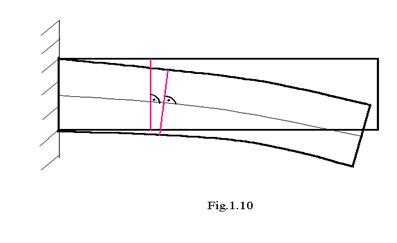
e) Ipoteza lui Bernoulli sau ipoteza sectiunilor plane
O sectiune plana normala pe axa elementului de rezistenta inainte de deformare ramane plana si normala pe axa si dupa deformare( fig. 1.10 )
f) Ipoteza suprapunerii efectelor
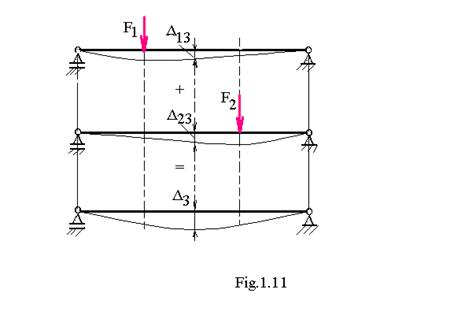
Deformatiile si tensiunile ce apar intr-un element de rezistenta sunt independente de ordinea aplicarii fortelor exterioare .Efectul total rezultand ca suma efectelor partiale produse de fiecare cauza .
Efectul total ( sageata , respectiv deformatia A ) rezulta ca suma a efectelor partiale produse de forta F3 (A
si efectul produs de forta F2 (A ),( fig.1.11) indiferent de modul sau succesiunea aplicarii fortelor
Rezultatul A este intotdeauna acelasi , indiferent de ordinea aplicarii fortelor , adica daca se aplica intai forta F3 si apoi F2 sau invers .
 ( 1 . 7 )
( 1 . 7 )
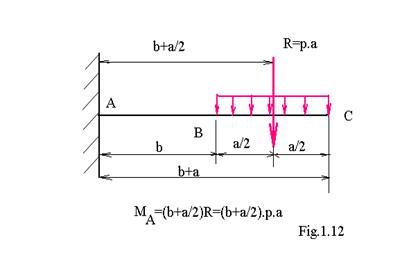
g) Ipoteza lui Saint Venant ( sau principiul lui Saint Venant )
Conform acestui principiu , inlocuirea unui sistem de forte prin rezultanta sa , cu toate ca produce modificari in starea locala de solicitare ( pe domeniul a - figura 1.12 ), aceasta ramane fara efect la distante mai mari . Aceasta ipoteza , permite , inlocuirea unei sarcini distribuite , prin rezultanta sa , rezultanta cu care se scrie apoi ecuatia de echilibru static .
1.8 DEFORMATII Si DelpasAri .
(aSPECTUL GEOMETRIC AL PROBLEMELOR DE REZISTENTA MATERIALELOR)
Sub actiunea fortelor exterioare corpurile solide se deformeaza , punctele lor deplasandu-se .Deformatia corpurilor poate fi elastica , daca dupa indepartarea cauzelor ce au produs defprmarea , corpul revine la forma si dimensiunile sale initiale .Deformatia poate fi elasto-plastica , sau plastica , daca corpul nu revine la forma si dimensiunile initiale , cand inceteaza actiunea fortelor exterioare , ramanand cu deformatii numite remanente .Deformatiile corpurilor depind de o serie de factori precum : caracteristicile mecanice ale materialului din care este confectionat , forma si dimensiunile sale , marimea si modul de aplicare al fortelor exterioare .
DEFORMATII LINIARE
Se considera bara din figura 1.13 , solicitata la intindere de o forta axiala F . In bara se produc :
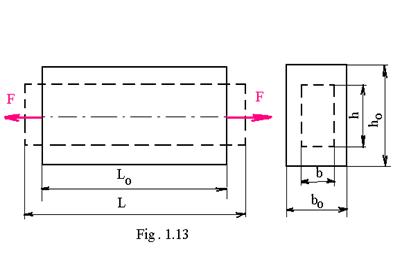
n o deformatie longitudinala - lungire
![]() ( 1 . 8 )
( 1 . 8 )
n o deformatie transversala - scurtare
![]() ( 1 . 9 )
( 1 . 9 )
Dimensiunile Lo , bo , ho , L , b , h sunt dimensiunile initiale , respectiv finale ale barei .
Deformatia unitatii de lungime a barei poarta numele de deformatie specifica a - lungire specifica sau alungire .
![]() ( 1 . 10 )
( 1 . 10 )
S-a demonstrat experimental , ca deformatiile specifice transversale atr ( contractii specifice sau scurtari specifice ) sunt proportionale cu deformatia specifica longitudinala prin intermediul coeficientului lui Poisson , sau , coeficientul de contractie transversala in urmatorul mod :
![]() ( 1 . 11 )
( 1 . 11 )
Coeficientul lui Poisson are pentru cele mai multe materiale valoarea 0,3 .
In cazul in care , forta F solicita bara la compresiune , marimile AL , si a poarta numele de scurtare , respectiv scurtare specifica
Deformatiile specifice sunt marimi adimensionale .
LUNECAREA SPECIFICA
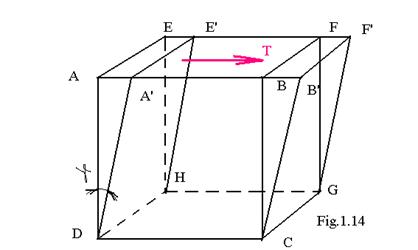
Se considera un element de volum paralelipipedic ABCDEFGH ( fig.1.14 ) cu latura egala cu unitatea . Fata de jos este fixa ( imobilizata ) . Pe fata de sus actioneaza o forta taietoare , ce produce pe fetele cubului tensiuni tangentiale , cu sensurile indicate in figura 1.14 . Datorita acestor tensiuni , fata ABFE luneca paralel cu ea insasi , ajungand in pozitia A'B'F'E'. Aceasta lunecare poate fi masurata prin unghiul g dintre fetele , si masoara variatia unghiului de 90 si se numeste lunecare specifica , sau deformatie unghiulara specifica
Lunecarea specifica se considera pozitiva cand are loc o micsorare a unghiului de 90 si negativa in caz contrar . Este o marime adimensionala ( se masoara in radiani ).
1.8.3 DEPLASARI
Sub actiunea fortelor exterioare , corpurile solide se deformeaza . Punctele lor isi schimba pozitia in timpul solicitarilor exterioare . Drumul parcurs in decursul procesului de deformatie de un punct al unui element de rezistenta , se numeste deplasare .
1.9 RELATII Intre tensiuni Si deformaTii SPECIFICE .
CURBA CARACTERISTICA . LEGEA LUI HOOKE
( ASPECTUL FIZIC AL PROBLEMELOR REZISTENTEI MATERIALELOR )
Aspectul fizic al problemelor rezistentei materialelor stabilesc legatura dintre aspectul static , adica dintre tensiunile ce apar : sau si aspectul geometric , adica deformatiile specifice . Aceasta dependenta se determina prin incercari de laborator , pentru fiecare tip de material in parte .
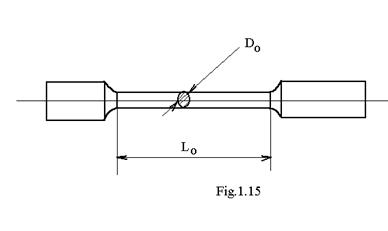
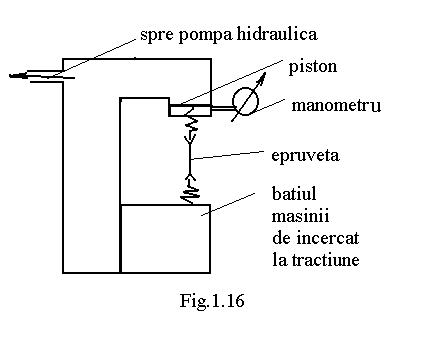
Legatura dintre si a se stabileste prin incercarea la tractiune , prevazuta in STAS 200/87. Incercarea se realizeaza pe esantioane de material , numite epruvete (fig.1.15) , a caror forma si dimensiuni este stabilita prin STAS-ul amintit , la fel ca si , modul lor de prelucrare al suprafetelor , temperatura mediului inconjurator , la momentul si in locul in care se face incercarea , umiditatea aerului , viteza de incarcare , utilajul cu care se realizeaza incarcarea , precum si elementele ce trebuiesc determinate , definirea si modul lor de determinare .
Epruvetele se fixeaza in batiul unei masini de incercat la tractiune ( fig.1.16 ) ce aplica epruvetei o forta uniform crescatoare , dirijata dupa axa acesteia . Masina este inzestrata cu un dispozitiv de masurate a fortei ( in Newtoni ) si a deformatiilor ( extensometru ) in fiecare moment i:
 ( 1 . 12 )
( 1 . 12 )
( Vezi lucrarea de laborator nr.1 )
Exista
masini
la care in
urma inregistrarilor
efectuate se poate direct trasa diagrama de variatie ![]() , diagrama care pentru otelul de uz
general , sau otelul
moale are aliura din figura 1.17 .
, diagrama care pentru otelul de uz
general , sau otelul
moale are aliura din figura 1.17 .
Valorile punctelor caracteristice din diagrama sunt diferite in functie de dimensiunile pe care le are epruveta .
Pe aceasta diagrama se disting urmatoarele zone :
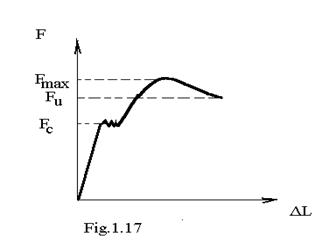
a) - forta este proportionala cu deformatia : ![]() ; este
aplicabila legea lui Hooke ( ce urmeaza a fi enuntata
; este
aplicabila legea lui Hooke ( ce urmeaza a fi enuntata
b) - o portiune de palier orizontal , cand deformatia creste fara ca forta sa creasca vizibil , eventual , sa oscileze in jurul unei valori constante - Fc - numita forta de curgere ;
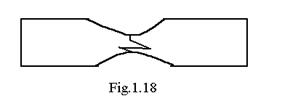
c) -urmeaza un proces de intarire a materialului - ecruisare - forta creste pana la valoarea maxima Fmax , moment in care apare g ituirea epruvetei (fig.1.18 ) adica micsorarea sectiunii acesteia . Rezistenta epruvetei scazand datorita micsorarii sectiunii acesteia , forta de tractiune a masinii scade, epruveta rupandu-se la o valoare ultima a fortei Fu , mai mica decat cea maxima . In figura 1.18 , se observa modul de rupere al epruvetei : in centru , spre exa acesteia , sectiunea de rupere este perpendiculara pe axa epruvetei ( caracter de rupere al materialelor ductile ) iar spre exterior , sectiunea de rupere este inclinata fata de axa epruvetei ( caracteristic materialelor fragile ) . Deci , caracterul ruperii este mixt : ductilo-fragil .
Diagrama : ![]() poate fi
trasata in marimi specifice :
poate fi
trasata in marimi specifice :
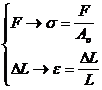 ( 1 . 13 )
( 1 . 13 )
Se va
obtine
diagrama ![]() , care va avea aceasi aliura
ca si diagrama F=f( AL ) , deoarece , atat
abscisa AL cat
si
ordonata F au fost impartite
la niste
valori constante : Ao , si
Lo .
, care va avea aceasi aliura
ca si diagrama F=f( AL ) , deoarece , atat
abscisa AL cat
si
ordonata F au fost impartite
la niste
valori constante : Ao , si
Lo .
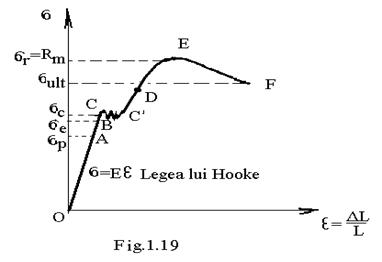
Se obtine astfel , caracteristica conventionala( fig.1.19) , numita astfel , deoarece , asa cum s-a vazut , impartirea se face la niste marimi constante , marimile initiale , ele variind in timpul incercarii in fiecare moment .
In aceasta caracteristica conventionala se deosebesc urmatoarele zone :
-de la O la A: caracterizata prin proportionalitatea dintre tensiune si deformatie a Este valabila legea lui Hooke , pana la o valoare a tensiunii , notata p , nimita limita de proportionalitate ;
Ecuatia liniei drepte OA , din figura 1.19 se scrie :
![]() ( 1 . 14 )
( 1 . 14 )
si arata , ca , pana la limita de proportionalitate , tensiunea este proportionala cu deformatia , prin intermediul unui coeficient E , numit modul de elasticitate longitudinala sau modulul lui Young ( deoarece , a este adimensional , E are aceasi ecuatie de dimensiuni , respectiv unitate de masura ca si tensiunea , respectiv , N/mm2 ) .
Aceasta enuntare reprezinta legea lui Hooke , si reprezinta relatia fundamentala a teoriei elasticitatii . Pentru oteluri , valoarea medie a modulului de elasticitate longitudinala E , este 2,1.105 N/mm2 .In tabelul 1 .1 sunt date caracteristicile mecanice , constantele elastice si fizice ale diferitelor materiale .
-de la A la B materialul se comporta elastic , adica , dupa incetarea actiunii fortei , epruveta deforata , revine la forma si dimensiunile initiale , ne prezentand deformatii remanente . Ordonata punctului B se numeste limita de elasticitate e . Practica a demonstrat ca nu exista materiale perfect elastice , si ca ,sub orice sarcina , oricat de mica , materialul primeste deformatii permanente ;
intre punctele C si C' , alungirea epruvetei are loc la sarcina constanta , sau usor variabila in jurul unei valori . Curba prezinta un palier orizontal in primul caz , sau sinuos in cel de al doilea caz , numit palier de curgere , valoarea tensiunii se numeste limita de curgere c
-din punctul C' , curba caracteristica are un traseu ascendent CE numit zona de intarire .Valoarea tensiunii corespunzatoare fortei maxime de rupere :
![]() ( 1 . 15 )
( 1 . 15 )
se numeste limita de rupere r sau rezistenta la rupere Rm
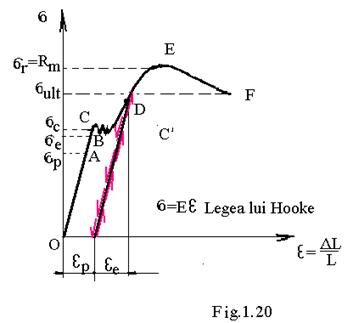
Daca in punctul D din intervalul C'E inceteaza actiunea fortei , epruveta nu mai revine la forma si dimensiunile initiale ( curba de descarcare reincarcare fiind cea din figura 1.20 pe o portiune paralela cu zona de proportionalitate ) . Deci , deformatia specifica totala at corespunzatoare punctului D este formata dintr-o deformatie specifica elastica ae si una plastica , remanenta ap
![]() ( 1
. 16 )
( 1
. 16 )
- cand sarcina se apropie de valoarea maxima Fmax epruveta se gatuie , gatuire ce se dezvolta din ce in ce mai mult , pana se produce ruperea . Dupa aparitia gatuirii , forta aplicata epruvetei scade , ceea ce duce la portiunea descendenta a curbei .Daca in aceasta zona , forta s-ar imparti la sectiunea din zona gatuita , raportul lor ar creste , ne-am situa in zona ascendenta , corespunzatoare liniei punctate din digrama din figura 1.20- ceea ce ar corespunde situatiei reale . Daca dupa rupere , se aseaza cele doua bucati de epruveta cap la cap , si se masoara distanta ultima dintre repere Lu , se determina alungirea , sau lungirea specifica la rupere :
![]() (1 . 17 )
(1 . 17 )
In practica , alungirea la rupere se da in procente , se noteaza cu A , insotit de 5 , sau 10 :
![]() ( 1 . 18 )
( 1 . 18 )
Indicele n se ia
egal cu 10 la epruveta lunga , la care ![]() , si
respectiv , 5 cand
acest raport este egal cu cinci .
, si
respectiv , 5 cand
acest raport este egal cu cinci .
Masurand diametrul dupa rupere du , se calculeaza aria ultima Au , iar cu ajutorul ei se determina gatuirea la rupere :
![]() ( 1 . 19 )
( 1 . 19 )
Cele patru marimi definite anterior , limita de curgere , limita de rupere , alungirea la rupere , gatuirea la rupere , poarta numele de caracteristici mecanice ale materialului . Determinarea lor se face in laborator , iar cunoasterea lor este foarte importanta pentru calculul de rezistenta si pentru utilizarea corecta a materialului .
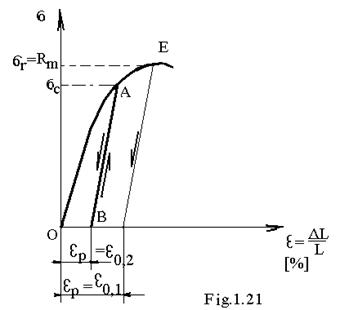
Pentru otelul aliat , curba caracteristica , nu prezinta palier orizontal , ceea ce face ca limita de curgere aparenta c sa nu poata fi stabilita In asemenea cazuri , se defineste limita de curgere conventionala sau Rp0,2 ,(sau limita de curgere tehnica ) ca valoare a tensiunii careia il corespunde dupa descarcare o lungire specifica permanenta de 0,2 % (fig.1.21) . Se constanta ca in cursul descarcarii , intre si a exista o relatie de legatura liniara , paralela cu portiunea de proportionalitate initiale .
PROPRIETATILE MECANICE ALE MATERIALELOR
Proprietatile mecanice ale materialelor se pot clasifica dupa cum urmeaza :
a) dupa comportarea materialului in urma indepartarii sarcinilor se deosebesc :
- materiale elastice a caror deformatii dispar in urma incetarii actiunii fortei ;
- materiale plastice , care se caracterizeaza prin ezistenta deformatiilor remanente (permanente ) deformatii ce nu dispar o data cu indepartarea sarcinilor exterioare ;
- materiale elasto-plastice cu deformatii atat elastice cat si plastice ( fiind valabila relatia 1.16 );
b) dupa marimea deformatiilor inainte de rupere exista
-materiale tenace care sufera deformatii mari inaintea ruperii ( se mai numesc materiale ductile ) ele prezentand in caracteristica conventionala palier de curgere (fig.1.20 );
-materiale fragile caracterizate prin deformatii foarte mici ( sau deloc ) inaintea ruperii ( fig.1.21);
c) dupa valoarea constantelor elastice E , G si masurate pe diferite directii :
-materiale izotrope , la care constantele elastice au aceleasi valori dupa toate directiile ;
-materiale anizotrope , cu comportari elastice diferite .
1.11 REZISTENTE ADMISIBILE
COEFICIENTI DE SIGURANTA
In timpul functionarii elementele de rezistenta , piesele unui mecanism , a unei masini sunt solicitate . Se ridica intrebarea : pana la ce valoare poate ajunge incarcarea piesei : pana cand in elementul de rezistenta se atinge valoarea tensiunii de curgere c sau pina la rupere ?
Daca s-ar ajunge la valoarea tensiunii de curgere ,piesa ar prezenta deformatii remanente ce ar afecta dimensiunile acesteia , modificind conditiile initiale , iar pana la rupere nici nu poate fi vorba !
Pe baza unei indelungate experiente , de proiectare si exploatare , s-a ajuns la concluzia ca , tensiunile efective (reale ) din elementul de rezistenta , sa fie mai mici decat a valoare maxima , numita rezistenta admisibila aleasa astfel incat sa fie respectate conditiile de rezistenta , rigiditate si stabilitate ale elementului de rezistenta
Rezistenta admisibila se noteaza cu a ( sau a si este :
![]() ( 1 . 20 )
( 1 . 20 )
in care crit se ia in functie de material, din curba caracteristica in modul urmator :
-pentru materiale ductile sau tenace ( oteluri de rezistenta mica si mijlocie , cu deformatii mari inaintea ruperii ) , crit c , respectiv:
![]() ( 1 . 21 )
( 1 . 21 )
-pentru materiale fragile ( materiale ceramice ,fonta , otelurile aliate ) fara deformatii inaintea ruperii . crit r, respectiv :
![]() ( 1 . 22 )
( 1 . 22 )
Cc si Cr sunt coeficienti de siguranta la alegerea carora se tine seama de o serie de factori precum : importanta piesei , natura , temperatura si durata de functionare , felul , tipul sarcinii aplicate , etc.
Copyright © 2025 - Toate drepturile rezervate