 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
DEFORMATIILE BARELOR DREPTE SOLICITATE LA INCOVOIERE
1 generalitATi
Prin solicitarea de incovoiere , barele se deformeaza si iau forme curbe . Studiul acestor deformatii se impune datorita urmatoarelor considerente :
-in toate cazurile de rezolvare a problemelor static nedeterminate la incovoiere este necesar sa apelam la relatiile de deformare ;
-exista situatii in care barele solicitate la incovoiere trebuie sa indeplineasca unele conditii limita de deformare .
Studiul deformatiilor barelor drepte solicitate la incovoiere se face asupra axei barei , care dupa deformare poarta numele de fibra medie deformata .
Se considera o bara dreapta , simplu rezemata , solicitata la incovoiere de un sistem de forte ce actioneaza in planul sectiunii transversale : Fi ( i=1,2,.,n) , ( figura 1 ).
Starea de deformatie a unei sectiuni de abscisa x (fig.1 ) :, se caracterizeaza prin urmatoarele marimi geometrice
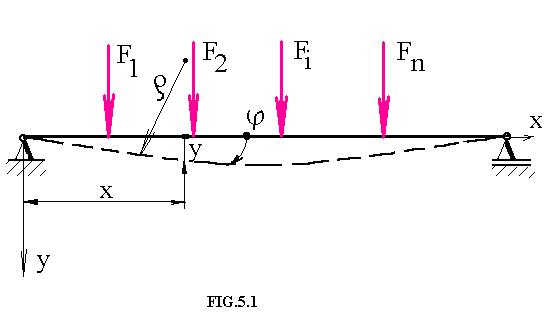
- deplasarea pe verticala
y=v , denumita sageata
, si
care rezulta
din ecuatia
fibrei medii deformate : ![]() ( 5 . 1 )
( 5 . 1 )
-rotirea sectiunii j , sau inclinarea fibrei medii deformate , care se obtine din derivarea ecuatiei fibrei medii deformate :
![]() ( 5 . 2 )
( 5 . 2 )
-raza de curbura r a fibrei medii deformate .In geometria diferentiala se demonstreaza:
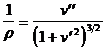 ( 5 . 3 )
( 5 . 3 )
unde : 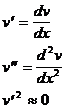 ( 5
. 4 )
( 5
. 4 )
relatia ( 3 ) devine :
![]() ( 5
. 5 )
( 5
. 5 )
Dar din relatia lui Navier se poate scrie :
![]() ( 5 . 6 )
( 5 . 6 )
rezulta ca :
![]() ( 5 . 7 )
( 5 . 7 )
Din figura ( 5 . 1 ) rezulta ca derivata a doua a ecuatiei fibrei medii deformate este negativa , cand momentul incovoietor este pozitiv.Prin urmare in relatia ( 5 .7 )trebuie introdus semnul ( - ) :
![]() (5 . 7' )
(5 . 7' )
unde M , reprezinta momentul incovoietor ce deformeaza bara.
In cazul solicitarii de incovoiere pura , M=const , deci deformatia are loc dupa un arc de cerc .
Daca modulul de rigiditate la incovoiere E Iz este constant , tinand cont de relatiile diferentiale intre eforturi ,ecuatiile diferentiale aproximative de ordin superior ale fibrei medii deformate sunt :
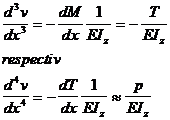 ( 5 . 8 )
( 5 . 8 )
Studiul deformatiilor se bazeaza pe efectuarea integrarii ecuatiei ( 5 . 7' ) .Se obtin astfel :
Deformatia unghiulara
![]() ( 5 . 9 )
( 5 . 9 )
Sageata
![]() ( 5 . 10 )
( 5 . 10 )
C1 ,C2 fiind constante de integrare ce se determina din conditiile initiale :
- in articulatie si reazem simplu , sageata este nula ;
- in incastrare , unghiul si sageata sunt nule .
Integrarea analitica a ecuatiei fibrei medii deformate se recomanda in cazurile in care bara are o incarcare simpla , unul , doua campuri ( tronsoane ) . La trecerea de la un tronson la altul , trebuiesc respectate conditiile de continuitate: sageata si unghiul de ratatie sa aibe aceleasi valori la limita dintre cele doua tronsoane .
In punctul in care momentul invovoietor se anuleaza , fibra medie deformata are punc de inflexiune ( isi schimba curbura ).
Exemple DE CALCUL
In continuare se vor studia cateva exemple simple de calcul al deformatiilor la incovoiere :
EXEMPLUL 1
Calculul deformatiilor la o bara incastrata la un capat , libera la celalalt , solicitata de o forta concentrata la capatul liber .( figura 5 . 2)
In sectiunea situata la distanta x de capatul liber B , momentulincovoietor este :
![]() ( 5
. 11 )
( 5
. 11 )
Ecuatia fibrei medii deformate devine :
![]() ( 5 .12 )
( 5 .12 )
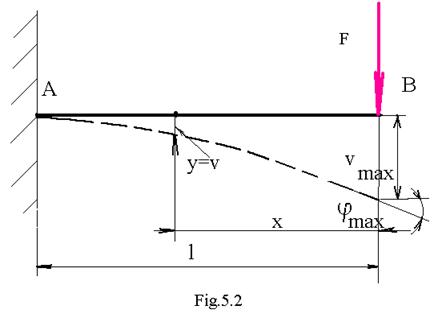
Calculul deformatiei unghiulare :
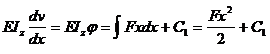 (5 . 13 )
(5 . 13 )
x=l => j
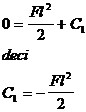 (5 . 14 )
(5 . 14 )
Deci : 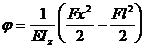 ( 5 . 15 )
( 5 . 15 )
Rotirea maxima se produce in incastrare , pentru x=0 :
![]() ( 16
)
( 16
)
Calculul deformatiei pe verticala ( sagetii )
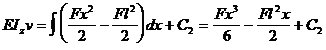 (5 . 17 )
(5 . 17 )
x=l => v=0 :
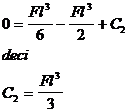 (5 . 18 )
(5 . 18 )
Deci : 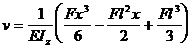 (5 . 19 )
(5 . 19 )
Sageata maxima are loc la capatul liber , pentru x=0:
![]() (5 . 20 )
(5 . 20 )
EXEMPLUL 2
Calculul deformatiilor la o bara dreapta incastrata la un capat , libera la celalalt , actionata de o forta uniform distribuita pe toata lungimea ( Fig.3):
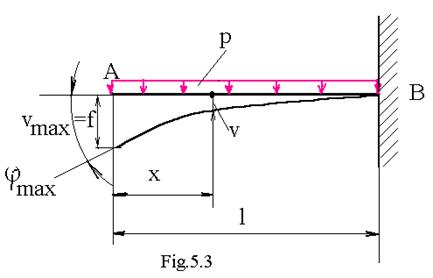
Momentul incovoietor in sectiunea x este :
![]() (5 . 21 )
(5 . 21 )
Ecuatia fibrei medii deformate devine :
![]() ( 22 )
( 22 )
1) Calculul deformatiei unghiulare :
![]()
x=l => j
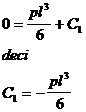 ( 23
)
( 23
)
Deci : 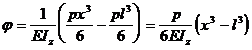 ( 5
. 24 )
( 5
. 24 )
Rotirea maxima are loc in incastrare , pentru x=0:
![]() ( 25 )
( 25 )
. Calculul deformatiei pe verticala ( sagetii )
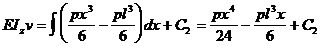 (5 . 26 )
(5 . 26 )
x=l => v=0
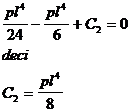 (5 . 27 )
(5 . 27 )
Deci sageata este :
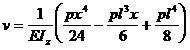 ( 5 . 28 )
( 5 . 28 )
iar sageata maxima din capatul liber este :
![]() (5 . 29 )
(5 . 29 )
EXEMPLUL 3
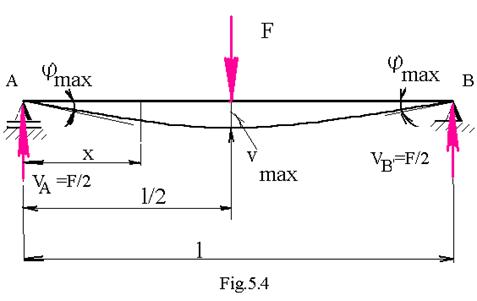
Calculul deformatiilor pentru bara simplu rezemata , solicitata de o forta concentrata la mijloc(fig.4 ).
Intr-o sectiune curenta situata la distanta x de reazemul simplu , momentul incovoietor este :
![]() ( 5 . 30 )
( 5 . 30 )
Ecuatia fibrei medii deformate devine :
![]() ( 5 . 31 )
( 5 . 31 )
Calculul deformatiei unghiulare
![]() ( 5 . 32 )
( 5 . 32 )
x=l/2 , j
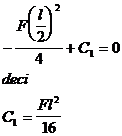 ( 33 )
( 33 )
deci:
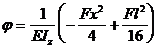 ( 34 )
( 34 )
Rotirile maxime se obtin in reazeme :
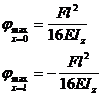 ( 35 )
( 35 )
Calculul deplasarii pe verticala ( sagetii)
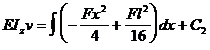 ( 5
.36)
( 5
.36)
( 5 . 36')
Din conditiile
la limita
se determina
x=0 , x=l , => C2=0.
Deci:
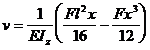 ( 37 )
( 37 )
Sageata maxima se obtine la jumatatea barei , pentru x=l/2 :
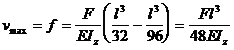 (5 . 38 )
(5 . 38 )
EXEMPLUL 4 Calculul deformatiilor pentru o bara simplu rezemata , solicitata de o sarcina uniform distribuita pe toata lungimea ei ( fig.5 ):
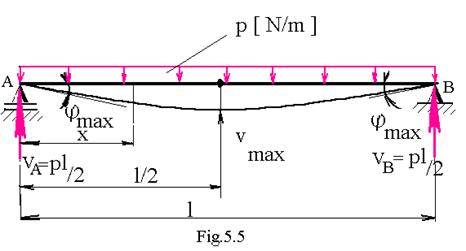
Momentul incovoietor in sectiunea situata la distanta x de reazemul simplu este :
![]() ( 39
)
( 39
)
Ecuatia fibrei medii deformate devine :
![]() ( 40
)
( 40
)
Calculul deformatiei unghiulare
![]()
![]() ( 5 . 41 )
( 5 . 41 )
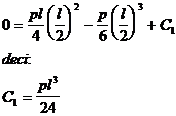 ( 5 . 42 )
( 5 . 42 )
Deci : 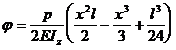 ( 5 . 43 )
( 5 . 43 )
Rotirea maxima are loc in reazeme :
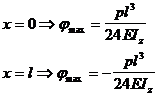 (5 . 44 )
(5 . 44 )
Calculul deplasarii pe verticala ( sagetii )
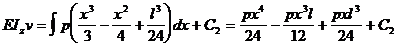 ( 45 )
( 45 )
Deci : 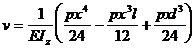 (5 . 46 )
(5 . 46 )
Sageata maxima se obtine la mijlocul barei , pentru x=l/2 :
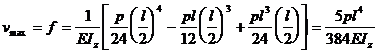 (5 .47)
(5 .47)
OBSERVATII
Calculul deformatiilor prin integrarea ecuatiei diferentiale a fibrei medii deformate este dificil in cazul in care apar mai multe solicitari in lungul barei . De aceea se adopta metode mai simple de calcul . Una dintre aceste metode este cea a barei conjugate sau metoda barei reciproce .
METODA BAREI RECIPROCE PENTRU CALCULUL DEFORMATIILOR
Prin bara reciproca sau bara conjugata se intelege , bara data initial incarcata cu o sarcina fictiva , sarcina fictiva pf , fiind diagrama de moment incovoietor din lungul barei:
![]() (5 . 48 )
(5 . 48 )
Ecuatia fibrei medii deformate devine :
![]() ( 5 . 49 )
( 5 . 49 )
Dar se cunoasc pentru incarcarea fictiva urmatoarele relatii diferentiale intre eforturi :
![]() ( 50 )
( 50 )
Daca pentru sarcina fictiva se construiesc diagramele de eforturi in lungul axei barei Tf si Mf rezulta :
![]() ( 51 )
( 51 )
Deci prin integrare :
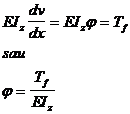 ( 52 )
( 52 )
sau : variatia deformatiei unghiulare in lungul axei barei solicitate la incovoiere , se obtine prin impartirea diagramei de forta taietoare fictiva la modulul de rigiditate la incovoiere Eiz .
Prin derivarea primei forme a relatiei ( 5 . 52 ) se obtine :
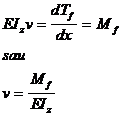 ( 53 )
( 53 )
sau : sageata
in
lungul axei barei solicitate la incovoiere
se obtine
impart
Aceste relatii sunt valabile in cazul in care constantele de integrare sunt nule . Cercetarile arata ca in cazul arelor incastrate le un capat , libere la celalalt , unghiul si sageata sunt nule in incastrare .Aceasta implica ca grinda reciproca sa aibe in acel punct forta taietoare si momentul incovoietor nule . Acest rezultat se obtine daca grinda reciproca are capatul liber acolo unde grinda reala are incastrarea , si incastrarea la capatul liber (figura6).
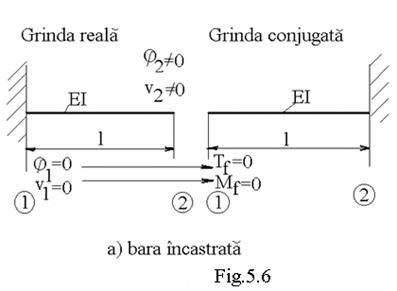
Deci :
-reciproca barei incastrate este tot o bara incastrata la capatul liber al grinzii reale si libera la capatul incastrat ( figura 6 );
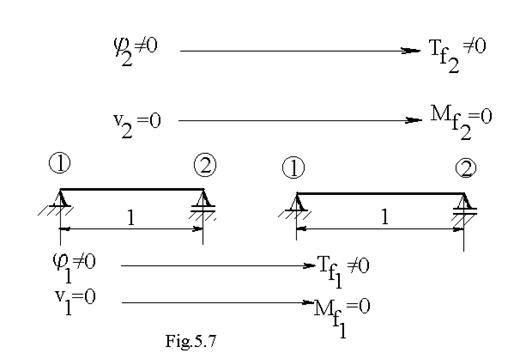
-reciproca barei simplu rezemata este tot o bara simplu rezemata ( figura 7 );
-reciproca unei bare cu doua reazeme simple si cu o consola la un capat este o grinda la care reazemul simplu de la capat ramane reazem simplu , reazemul simplu intermediar devine articulatie , iar capatul liber al consolei devine incastrare .in mod analog se procedeaza la grinda cu doua console .
Metoda grinzii conjugate are dezavantajul ca , diagrama de moment devine o incarcare complexa , calculul fortei taietoare fictive si a momentului incovoietor fictiv devin dificil de calculat , deci , cu toate ca nu trebuiesc calculate constante de integrare,metoda se foloseste doar in cazul unor ncarcari simple .
EXEMPLUL NR . 1Calculul deformatiilor pentru bara simplu rezemata solicitata de o forta concentrata la mijloc ( figura 8 ) , prin metoda grinzii reciproce .
Sarcina totala ce actioneaza asupra grinzii reciproce( sarcina fictiva totala) :
![]() ( 5 . 54 )
( 5 . 54 )
Reactiunile grinzii reciproce sunt:
![]() ( 55 )
( 55 )
( grinda reciproca fiind simetrica din punct de vedere geometric si mecanic )
Prin urmare , unghiul pe reazem al grinzii este egal cu forta taietoare fictiva ( deci cu reactiunea grinzii reciproce ) impartite prin EIz :
![]() ( 5 .56)
( 5 .56)
Forta taietoare fictiva intr-o sectiune situata la distanta x de reazemul 1 va fi :
![]() (5 . 57 )
(5 . 57 )
Panta fibrei medii deformate intr-o sectiune oarecare va fi :
( 58 )
Se verifica in reletia ( 58 ) ca pentru x=l/2 => j
Momentul incovoietor fictiv este :
![]() (5 . 59 )
(5 . 59 )
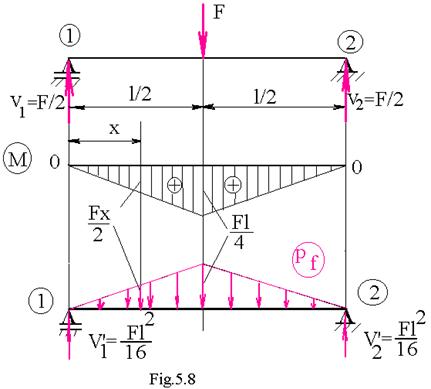
Sageata intr-o sectiune oarecare va fi :
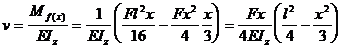 (5 . 60)
(5 . 60)
Sageata maxima se obtine pentru x=l/2:
![]() (5 . 61 )
(5 . 61 )
4 CALCULUL DEFORMATIILOR DE INCOVOIERE
CU AJUTORUL PRINCIPIULUI SUPRAPUNERII EFECTELOR
In cazul in care incarcarea este complexa , diagramele de eforturi de asemenea devin complexe , calculul deformatiilor este greoi . De aceea se poate aplica cu succes principiul suprapunerii efectelor :
Daca asupra unui element de rezistenta actioneaza sistemul de forte F1 ,intr-o sectiune sageata este v1 , daca asupra aceluiasi element actioneaza sistemul de forte F2 , sageata in aceeasi sectiune este v2. Cand cele doua sisteme de forte actioneaza simultan , in sectiunea mentionata , sageata se va putea calcula prin insumarea celor doua sageti calculate in mod independent :
![]() ( 62 )
( 62 )
EXEMPLU Pentru bara incastrata din figura 9 sa se calculeze sageata maxima .
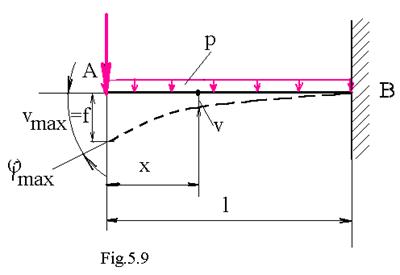
Asa cum s-a spus , deformatia maxima se poate calcula insumand relatiile : (5 . 20 ) si (5 . 29 ) pentru calculul sagetii maxime :
![]() ( 5 . 63 )
( 5 . 63 )
si a relatiilor ( 16 ) cu (5 . 25 ) pentru calculul rotirii maxime :
![]() ( 5 . 64 )
( 5 . 64 )
Copyright © 2026 - Toate drepturile rezervate