Asamblari demontabile - clasificare, utilizare, material

ASAMBLARI DEMONTABILE

Prin asamblare demontabila se intelege un ansamblu, o piesa complexa, instrument, care se poate desface in piesele componente, fara a modifica forma sau caracteristicile functionale ale pieselor.

In cadrul acestei categorii, fac parte :

- asamblari filetate - deja analizate la capitolul 3 ;

- asamblari prin pene ;

- asamblari cu bolturi si stifturi ;

- asamblari conice prin presare ;

- asamblari cu inele tronconice ;

- asamblari prin caneluri ;

- asamblari bazate pe diferenta de dimensiuni.

1. ASAMBLARI PRIN PENE

Penele sunt organe de imbinare demontabile, care fixeaza sau regleaza pozitia a doua piese. Folosirea penelor prezinta avantajul realizarii unor asamblari simple si ieftine, dar, in acelasi timp slabesc rezistenta prin introducerea unor concentratori mari de tensiuni.

1.1. CLASIFICARE, UTILIZARE, MATERIAL

In tabelul 1. se prezinta o clasificare a penelor.

Datorita faptului ca sunt supuse la solicitari mari de incovoiere, forfecare, presiune de contact, penele se executa din OL60, OL70 si OLC45.

Rezistenta minima de rupere a materialelor din care se realizeaza penele trebuie sa fie de 60daN/mm˛.

Tabelul 1.

1.2. PENE TRANSVERSALE

Se prezinta in continuare cateva exemple de utilizare a penelor transversale.

In figura 1.- pene transversale pentru asamblare fara prestrangere. Se observa ca intre elementele 1 si 2 care trebuie asamblate cu ajutorul mansonului 5, exista un joc 'j'.

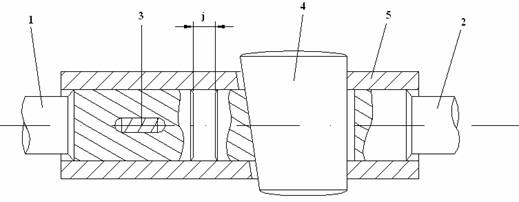
Fig 1.

Un exemplu de asamblare cu strangere este prezentata in figura 2. Pana 3 este presata astfel incat asigura contactul piesei 2 cu subansamblul 1 in care se monteaza.

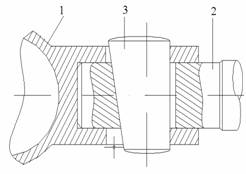
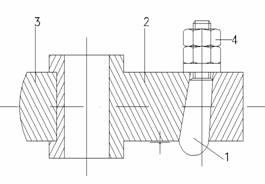
Fig 2.    Fig 3.

In figura 3. se prezinta un exemplu de asamblare de reglare. Pana 1 a carei pozitie poate fi riguros controlata cu ajutorul piulitelor 4, prin deplasarea sus-jos, imprima cuzinetului 2 o miscare stanga-dreapta in lagarul 3, obtinandu-se astfel reglarea la pozitie a cuzinetului.

1.2.1. CONSIDERATII TEORETICE SI ELEMENTE DE CALCUL

Pentru buna functionare a penelor transversale, este necesar ca acestea sa se mentina in imbinare in timpul exploatarii, sa se asigure deci autofixarea, sau autofranarea penelor in locasul lor.

Constructiv, acest lucru se poate realiza prin limitarea unghiurilor de inclinare a fetelor penei la valorile obisnuite din conditia de autofranare.

Schema de calcul se prezinta in figura

Fig 4

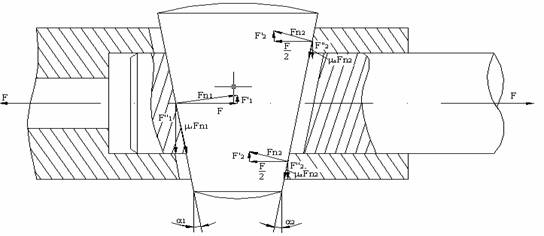
Dupa cum se poate observa, in figura sunt prezentate fortele intr-o asamblare fara pre-strangere.

Se face ipoteza simplificatoare ca se pot neglija componentele orizontale ale fortelor de frecare.

In aceasta situatie, conditia de autofixare devine:

F'1 + 2 F'2 ≤ F''1 + 2 F''2    (1)

Dar,

F'1 = F·tg α1

2 F'2 = 2 tg α2 = F·tg α2

F''1 = μ1·Fn1·cos α1

2 F''2 = 2 μ2·Fn2·cos α2

Dar,

Fn1 =

Fn2 =

Deci relatia (1.) devine :

F·tg α1 + F·tg α2 ≤ F·μ1 + F·μ2    (2)

In relatia (2) : μ1 = tg ρ1 si μ2 = tg ρ2 unde ρ1 si ρ2 sunt unghiuri de frecare.

In final se obtine :

tg α1 + tg α2 ≤ tg ρ1 + tg ρ2

(3)

Relatia (3) prezinta conditia de autofranare, si spune ca autofranarea este asigurata atunci cand suma unghiurilor de inclinare este mai mica decat suma unghiurilor de frecare.

Pentru penele cu o singura fata inclinata :

α1 = α ; α2 = 0 si (3) devine :

α ≤ ρ1 + ρ2 ; sau (4)

α ≤ 2ρ , daca ρ1 = ρ2 = ρ

In tabelul 2 se prezinta valorile recomandate pentru unghiurile de inclinare a penelor.

Tabel 2.

In cazul asamblarilor cu prestrangere initiala, trebuie determinata forta de introducere a penei, F' care este necesara realizarii fortei de prestrangere F0. Schema de calcul este prezentata si in figura 5.

Fig 5.

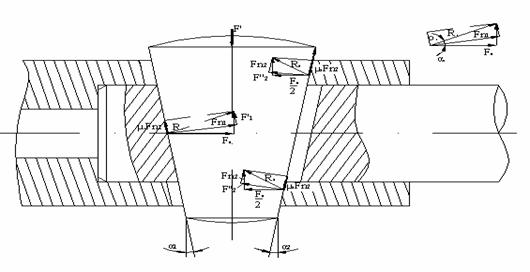
Forta F0 de prestrangere este proiectia pe orizontala a rezultantelor R1 si R2. Aceste rezultante, se obtin din suma vectoriala a fortelor Fn1, Fn2 cu fortele de frecare μ1Fn1 si μ2Fn2, care apar la introducerea frontala a penei sub actiunea fortei F'.

Din conditia de echilibru, se scrie :

F' = F'1 + 2 F'2 (5)

Dar :    F'1 = F0·tg (α1 + ρ1)

F'2 = ˝ F0· tg (α2 + ρ2)

Relatia (5) devine : F' = F0·tg (α1 + ρ1) + F0· tg (α2 + ρ2) (6)

In situatia cea mai des intalnita, α1 = α , α2 = 0 , ρ1 = ρ2 = ρ si atunci relatia (6) devine :

F' = F0 [tg (α + ρ) + tg ρ]

Penele transversale fara strangere, si la care α1 = α2 = 0 prezinta o schema de incarcare ca cea din figura 6 , si se calculeaza la :

incovoiere, relatia de calcul fiind :

σi = = ≤ σai

forfecare, relatia de calcul fiind :

ζf = ≤ ζaf

solicitari de contact, cu relatia :

σs = ≤ σas    - manson-pana

σs = ≤ σas - arbore-pana

In relatiile de mai sus :

σai = ; c = 1,45.1,8

σaf = (0,2 + 0,3) σ 0,2

σas = 0,8 σ 0,2

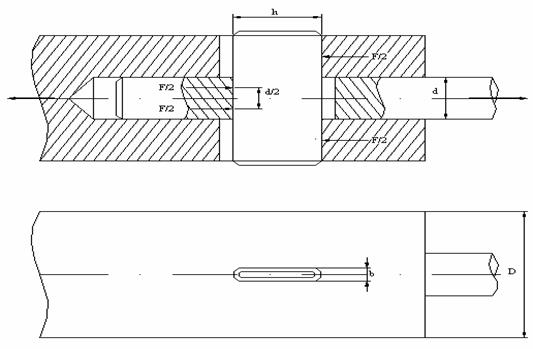
Fig 6.

1.3. PENE LONGITUDINALE

Forma de baza a penelor longitudinale este prezentata in figura 7.

Penele longitudinale se caracterizeaza prin faptul ca se monteaza paralel cu axa pieselor de imbinat.

Aceasta categorie de pene, se foloseste la asamblarea a doua piese coaxiale, cu scopul de a transmite miscarea de rotatie si moment.

Tipurile de pene longitudinale sunt reglementate de STAS 430-74, iar dimensiunile penelor in sectiune transversala, de STAS 431-81, 433-73, 434-73, 1004-81, 1007-81, 1006-71.

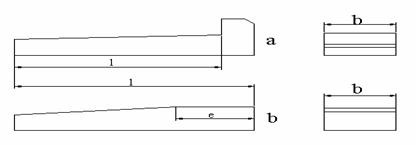
Fig 7.

In tabelul 3. se prezinta o clasificare mai detaliata decat cea din tabelul 1.

In continuare se prezinta pe scurt cateva tipuri de pene longitudinale :

a) - Pene inclinate

Acestea au fata dinspre butuc inclinata. Sub actiunea fortei de strangere, pana strange radial arborele si butucul. Aceste pene prezinta siguranta in exploatare, transmit momente mari, dar au dezavantajul ca produc ovalizari, dezaxari.

Penele inclinate pot avea diferite forme, capete drepte sau inclinate, cu nas sau fara nas. La penele cu nas, accesul pentru montare/demontare este posibil pe o singura parte.

b) - Pene inclinate subtiri

Aceste pene transmit momente mai mici decat cele anterioare, deoarece se inlocuieste canalul de pana din arbore cu o tesitura. Introduc concentratorii mici de tensiune, se recomanda pentru valori de diametru de pana la 230 mm. Se pot executa si in varianta cu nas.

c) - Pene inclinate concave

Acestea se ingroapa numai in butuc, transmit momente mici, se folosesc la diametre mai mici de 150 mm.

d) - Pene tangentiale

Se monteaza perechi, inclinarea fiind data suprafetei de contact dintre cele doua pene. Prin bataie una contra celeilalte, se produce o forta de apasare foarte mare, de aceea pot transmite momente foarte mari.

e) - Pene paralele

Au forma paralelipipedica si se monteaza cu joc radial.

Nu produc dezaxari, permit deplasarea pe arbore.

In cazul solicitarilor mari, pentru a evita smulgerea, penele paralele se fixeaza pe arbore cu suruburi.

f) - Pene disc

Partea ingropata in arbore este in forma de disc.

Avantajul este ca pot lua pozitia dupa butuc, prin balansare in locasul circular. Se recomanda la diametre de pana la 38 mm.

Formele constructive pentru penele de la punctele a.f sunt prezentate in anexa (A.1, figura AI.Ax).

Tabelul 3.

1.3.1. ELEMENTE DE CALCUL

a). Calculul asamblarilor cu pene inclinate

Datorita inclinarii penei, sub actiunea fortei de introducere F (figura 8) se creeaza forta de strangere Fr ce produce o reactiune intre butuc si arbore pe partea opusa.

In stare de repaos, Fr se poate considera uniform repartizata pe latimea penei - figura 9.a.

Sub actiunea momentului motor Mt si a celui rezistent, Mr, apare tendinta de rotire dintre butuc si arbore. In aceste conditii, luand in considerare si fortele de frecare, starea de repartizare a presiunilor pe latimea penei se modifica - figura 9.b.

In calcule, se neglijeaza fortele de frecare, si se considera o repartitie triunghiulara - figura 9.c.

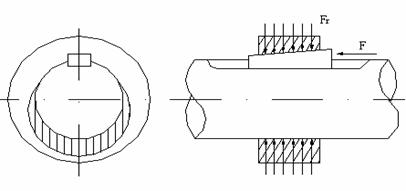
Fig 8.

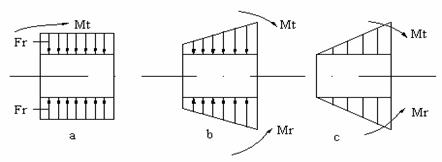
Fig 9.

a.1). Pana inclinata

In ipoteza ca pana asigura strangerea radiala necesara, schema de calcul este cea din figura 10.

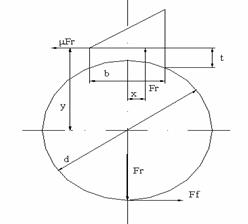
Fig 10.

Mt = Fr ·x + μ·Fr ·y + ˝ d·Ff    unde : (8)

Fr = ˝ b·l·p    p - presiunea de contact

l - lungimea penei

Daca    x = b ; y = d ; Ff = μ·Fr atunci :

Mt = b·l·pb + μb·l·pd + d·μb·l·p

Mt = b˛·l·p + μ· b·l·d·p + μ· b·l·d·p

Mt = b˛·l·p + μ· b·l·p·d

In final : Mt = b·l·p (9)

Mt - moment de torsiune transmisibil

Deoarece penele sunt standardizate, ele se aleg si se verifica, nu se dimensioneaza.

Verificarea se face in doua moduri :

calculand cu relatia 9. pe Mt care se compara cu momentul transmis in realitate, sau

se verifica presiunea de contact cu relatia :

pa (10)

a.2) Pana inclinata subtire

In fig. 11 se reprezinta repartizarea fortelor

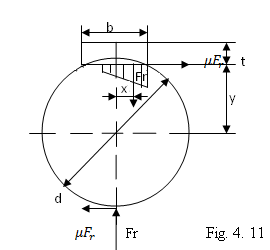
In aceleasi conditii, adica

Se obtine relatia de calcul 9.

Verificarea la presiunea de contact se face cu relatia 10.

Momentul transmisibil reprezinta aprox. 40% din momentul pe il poate transmite arborele.

a.3) Pana inclinata concava

Forta de strangere se repartizeaza uniform pe latimea penei,

(11)

Momentul transmisibil, se calculeaza cu relatia:

(12)

a.4) Pene tangentiale

Schema de calcul, se reprezinta in fig. 12.

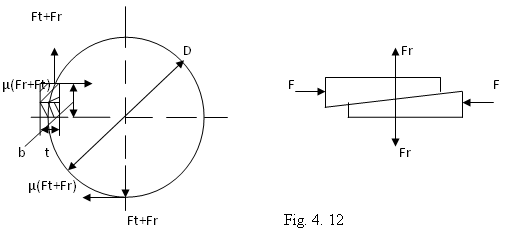
Daca Ft - forta periferica corespunzatoare momentului transmis, neglijand forta de stragere initiala Fr, valoarea momentului transmisibil va fi:

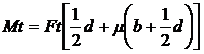(13)

In relatia 13, l - lungimea penei.

b) Indicatii privind pozitia penelor longitudinal cu strangere

In cazul cand o singura pana nu poate transmite momentul dat, sau cand lungimea necesara pentru o singura pana ar depasi valorile recomandate, 1<(1,5-2)d, se utilizeaza montarea mai multor pene.

Utilizarea a doua sau trei pene cu strangere, nu inseamna dublarea sau triplarea momentului de strangere, deoarece reactiunea rezultanta intre butuc si arbore nu creste in aceeasi masura. (fig. 13).

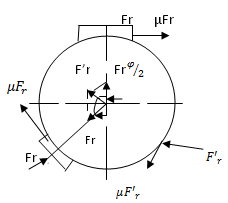
Fig. 13

Pozitia cea mai buna, atat pentru solidarizarea butucului cu arborele, cat si pentru ovalizare minima este .

c) Calculul asamblarilor cu pene paralele

Penele paralele se monteaza in locasul lor cu joc radial (fig. 14).

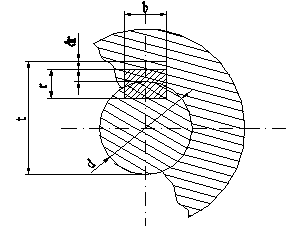Fig. 14

Din acest motiv, momentul este preluat si transmis doar de fetele laterale.

Schema de solicitare a unei pene paralele in functie de sensul de rotire al arborelului, este prezentata in figura 15.a

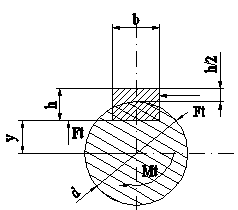Fig. 15.a

Momentul transmis se poate calcula cu relatia:

Mt=y.Ft sau, daca

Mt=d.Ft

Aceeasi relatie, se poate scrie si in functie de presiunea de contact.

Mt=y.p.A unde y - distanta fata de punctual de aplicare a fortei

P - presiunea unitara

A - suprafata ce transmite moment

Dar, y;Ah.l    deci,

Mt=h.l.p.d

In fig.15.b se prezinta repartizarea neuniforma a eforturilor de suprafetele de contact.

Neuniformitatea ,se formeaza pe de o parte datorita tendintei de scoatere a penei din locas , iar pe de alta parte , datorita existentei fortelor de frecare dintre suprafetele in contact.

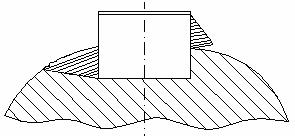
Fig. 15b

Penele paralele, se verifica la presiunea de contact si forfecare cu relatiile:

Pef= Pa

Ъef=Ъaf

d)Calculul asamblarilor cu pene disc

O asamblare cu pana disc este prezentata in fig.16

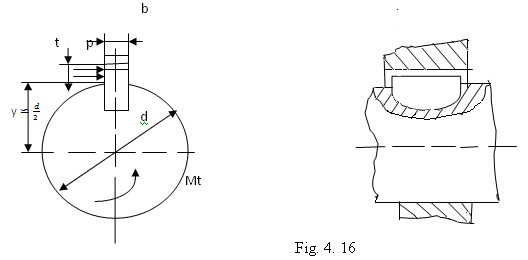
Momentul Mt transmisibil se calculeaza cu relatia:

Pana este solicitata preponderent la presiunea de contact pe suprafata si la forfecarea pe sectiunea

In tabelul 4 se dau valorile pentru presiunile de contact admisibile pentru calculul asamblarilor cu pene longitudinale.

Tabelul 4

2. Asamblari cu bolturi si stifturi

2.1 Asamblari cu bolturi

Bolturile sunt organe de masini in forma cilindrica folosite ca elemente de legatura in articulatii. Se construiesc in doua variante de baza:

-bolturi cu cap, in doua variante A si B - fig. 17

-bolturi fara cap, tot in doua variante - fig. 18

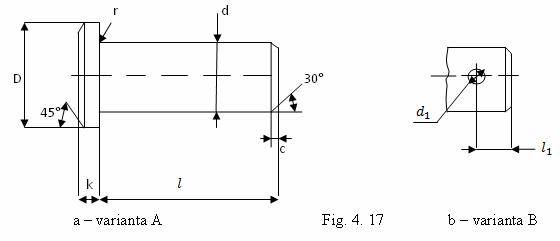
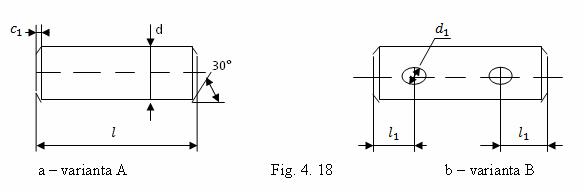
In constructia de masini, se folosesc si alte variante constructive de bolturi, cateva dintre acestea fiind prezentate in fig. 19.

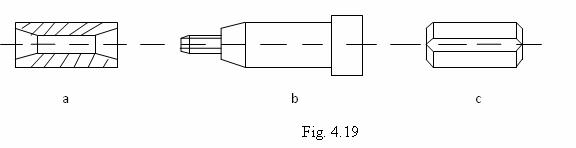
Ca materiale, se recomanda OL50, OLC35, OLC45, in funtie de solicitari.

Bolturile sunt solicitate la strivire, inconvoiere si forfecare. In calcule, se neglijeaza influenta jocurilor si a deformatiilor elastice asupra repartitiei sarcinilor, si se adopta schema de calcul din fig. 20.

a) 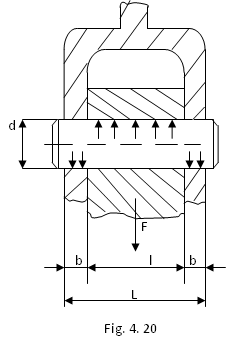     Solicitare de forfecare,

cu A - aria sectiunii de forfecare

b)      Solicitari de contact

δas    pentru strivirea intre bolt si tija.

δas    pentru strivirea intre bolt si furca

c)      Solicitare de inconvoiere cu W - modul de rezistenta al boltului

Valorile pentru tensiunile admisibile sunt:

2.2. Asamblari cu stifturi

Stifturile se folosesc in special, pentru a fixa pozitia relativa a doua piese.

In cazul solicitarilor mici, stifturile se pot inlocui cu pene si bolturi, care reprezinta solutii mai economice.

Formele de baza utilizate, sunt:

- stifturi cilindrice

- stifturi conice

Fiecare din cele doua categorii, pot fi: netede, sectionate, tubulare sau filetate. Formele constructive se prezinta in fig.21. - cilindrice, si fig.22. - conice.

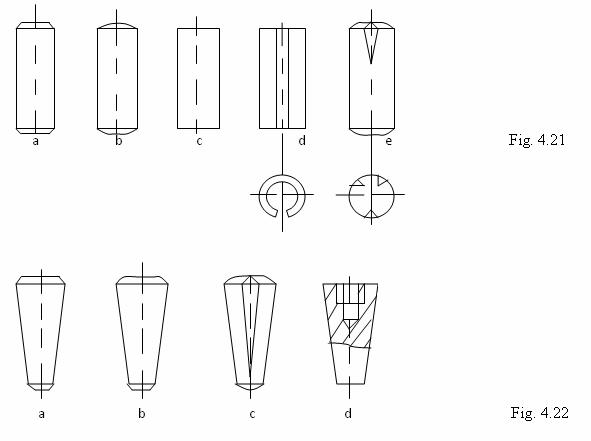
Stifturile de centrare se folosesc perechi, montate cat mai departe unul de altul. Stifturile conice, spre deosebire de cele cilindrice, nu isi pierd efectul de strangere in urma unor montari si demontari repetate, si se executa cu autofranare. In anexa (A.3) se prezinta exemple de utilizare a stifturilor conice si cilindrice.

Materialele recomandate, sunt: OL50, OLC45, OLC17, OSC 8.

Stifturile tubulare si cele spintecate se confectioneaza din otel de arc, cu

Stifturile sunt solicitate cu precadere la forfecare si solicitare de contact, calculele fiind generate de relatiile deja cunoscute. Astfel:

-solicitare de forfecare: , cu

Se va tine seama de numarul sectiunilor de forfecare - solicitare de contact:

pentru strivire intre stift si manson, si

pentru strivire intre stift si arbore.

In relatiile de mai sus, cu

d - diametrul stiftului

In tabelul 5 se indica valorile admisibile pentru eforturile unitare Pa, , in ipoteza sarcinilor statice. Pentru sarcini variabile, valorile se caracterizeaza cu un coeficient k=0,7 - sarcini pulsatorii sau k=0,5 - sarcini alternant simetrice.

Tabel 5

3. Asamblari conice prin presare

Schema de principiu pentru o asamblare de acest gen, este prezentata in fig. 4 23.

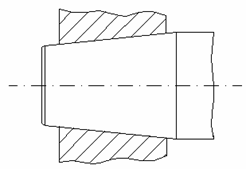Forta radiala necesara pentru asigurarea transmiterii momentului de torsiune fara patinare, este realizata fie prin exercitarea unei forte axiale cu ajutorul unei piulite, in cazul imbinarilor fara autoblocare (2 L>ρ), fie prin strangere proprie, prin crearea unui ajustaj conic cu strangere.

Fig. 23

In tabelul 6 se fac recomandari pentru conicitati in functie de cuplul de materiale din asamblare.

Pentru un element de portiune conica, forta normal elementara se va calcula cu relatia:

(27)

Tabelul 6

iar momentul de frecare elementar,

(28)

In cazul unei presiuni constante pe suprafata de contact:

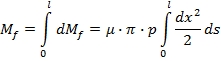
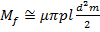(29)

Dar: deci

Semnificatiile notatiilor din relatiile 27, 28 si 29 se gasesc in fig. 2

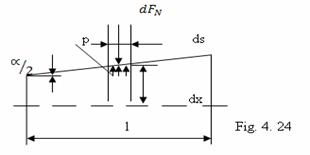
Pentru ca imbinarea sa transmita momentul Mt, trebuie sa fie indeplinita conditia:

sau

unde c - coeficient de siguranta .

Se poate scrie:

Din relatia de mai sus se poate obtine presiunea superficial minima:

Aceasta presiune se realizeaza datorita unei forte axiale de presare, care este, conform fig. 25.

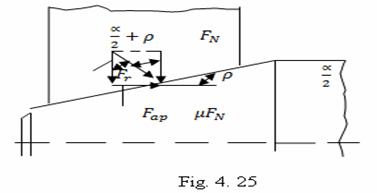
, sau

Se poate usor deduce relatia fortei de deplasare:

Avantajul principal al asamblarii conice prin presare, este ca se pot realiza diferentele de diametre ale celor doua piese (butuc-arbore) la o cursa mica, prin deplasarea axiala.

Dezavantejele sunt:

dificultatea calcularii exacte a tensiunilor axiale, radiale si tangentiale la ajustajele conice;

necesitatea realizarii unei conicitati riguros exacte la butuc si arbore.

5.1.5. Sudabilitatea metalelor

Sudabilitatea este caracteristica ce determina aptitudinea metalelor,in conditii de sudare date,de a realize asamblari.

Sudabilitatea este determinata de:

proprietatile metalului de baza;

tehnologia de sudare ;

conceptia constructiva a elementelor constructiei;

caracterul si nivelul solicitarilor in timpul exploatarii.

Referitor la sudabilitate, se mai folosesc si alte notiuni derivate,ca: siguranta la sudare si comportarea la sudare.

Compozitia chimica este elemental ce influenteaza determinant comportarea la sudare. Este motivul pentru care,respectarea retetei chimice devine obligatorie.

In cazul laminatelor din oteluri carbon obisnuite,se considera ca se asigura o comportare la sudare buna,fara masuri speciale,daca se respecta limitele din tabelul

Tabel 5.2.

Elementul cu cea mai mare influenta asupra comportarii la sudare,este carbonul.Odata cu cresterea continutului in carbon creste posibilitatea de calire, fapt care se evidentiaza prin aparitia in zona de sudare a unor zone de duritate mare.

In fig.5.2. se prezinta variatia duritatii de-a lungul unei linii,intr-o sectiune perpendiculara pe directia de depunere a unui strat de sudura.

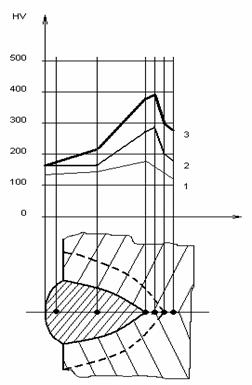Fig.5.2

O variatie a duritatii ca cea din figura 5.2. este caracteristica pentru sudurile realizate pe material laminat la cald,sau normalizat.

Se observa ca valorile maxime ale duritatii,cresc odata cu cresterea continutului de carbon. De asemenea,se remarca marirea diferentei dintre duritatea maxima atinsa si duritatea materialului de baza.

Cresterea continutului de carbon creste si pericolul formarii porilor in cusatura,datorita cresterii probabilitatii arderii carbonului,si deci a formarii de compusi gazosi in baia de metal topit.

Pentru a putea tine cont si de influenta cumulata a carbonului si a elementelor de aliere,asupra sudabilitatii,a fost necesara stabilirea unei metode cantitative de evidentiere a efectului studiat.

S-a introdus astfel,notiunuea de carbon echivalent C exprimata printr-o relatie liniara intre concentratiile diferitelor elemente.

In tabelul 5.3. sunt date,dupa HARDEN si VOLDRICH, limitele uzuale admise pentru C_e pentru care sudarea se face fara preincalzire.

In afara de C si grosimea pieselor de studiat,duritatea maxima admisa in zona influentata termic,depinde si de parametrii tehnologici.

Astfel, exista posibilitatea ca,prin adaptarea acestora,la specificul otelului sudat,sa se realizeze,o micsorare a duritatii maxime.

Tabel 5.3.

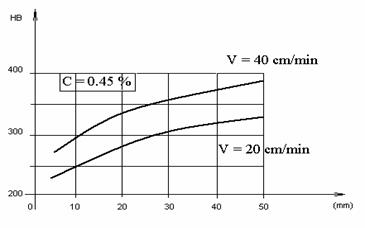
In figura 5.3. se observa influenta grosimii pieselor si avitezei de sudare asupra duritatii maxime din zona influentata termic.

In functie de valoarea carbonului echivalent si de tipul electrodului folosi,(acid sau basic) se determina cu ajutorul tabelului 5. un indice conventional de subunitate notat I.

Tabel

5.1.6. Clasificarea asamblarilor sudate

Asamblarile sudate pot fi realizate prin:

cusaturi cap la cap,sau

cusaturi in colt.

Simbolizarea asamblarilor sudate este prezentata in tabelul5.5.

Tabel 5.5

Reprezentarea,cotarea si notarea completa a sudurilor pe desene,este reglementata de STAS 735-87.

5.2.Calculul imbinarilor sudate

In calculul imbinarilor sudate se folosesc aceleasi principii si metode ca in rezistenta materialelor.Conditia initiala care se pune este principiul de egala rezistenta,adica imbinarile sudate sa aiba aceeasi rezistenta ca si restul constructiei.

In acest mod,se evita supradimensionarile.

5.2.1. Sudurile cap la cap

In figura 5. se prezinta o imbinare sudata cap la cap, ce constituie sectiunea de calcul.

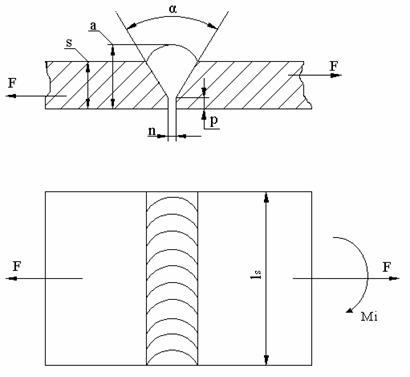
Fig.5.

Lungimea cordonului de sudura -1- este determinata de lungimea tablelor care se studiaza.

Datorita imperfectiunii cordoanelor de sudura la capete, se considera ca lungime de calcul:

l = l_s - 2∙s (5.2)

Grosimea cusaturii, -a- trebuie sa fie mai mare decat grosimea -s- a tablelor.

Pentru materialul de baza, forta maxima ce poate fi preluata cu incarcarea din figura, este:

F₁ = l_s ∙ s ∙ σ_a

Forta maxima preluata de cordonul de sudura:

F₂ = l ∙ a ∙ σ_as

Dar F₁ = F₂, deci l ∙ a ∙ σ_as = l_s ∙ s ∙ σ_a

Se obtine:

Deoarece l_s > l si σ_a > _as intr-adevar, a > s.

Practica recomanda pentru a:

a = (1.21.25) s (5.6)

Rezistentele admise ale cordonului - σ_as - comparativ cu materialul de baza - σ_a - , sunt:

pentru tractiune : σ_{as a}

pentru compresiune : σ_{as a}

Daca (fig.5.4) sudura este solicitata si de moment un momentul incovoietor Mi, atunci efortul unitar in cursatura, va fi :

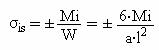
Daca cordonul va fi supus simultan si fortei F si momentului Mi, efortul unitar va fi :

Pentru solicitarea la forfecare a sectiunii :

5.2.8. Deformatii si tensiuni remanente

5.2.8.1. Originea deformatiilor si tensiunilor remanente

Tensiunile remanente ce apar in piesele sudate se datoreaza variatiilor de temperatura la care este supusa piesa in timpul sudarii.

Daca incalzirea si racirea se fac uniform, in tot corpul piesei, iar dilatarea si contractia sunt libere, starile de eforturi si modificarile de volum cauzate de incalzire sunt reversibile la racire. Conditiile de mai sus, nu pot insa sa fie asigurate .

Efectele incalzirii locale produse in timpul sudarii pot fi reversibile, in situatia in care tensiunile provocate de incalzirea locala si neuniforma nu ar depasi limita de elasticitate a metalului.

Trecandu-se in domeniul plastic, metalul ramane dupa racire , cu deformatii si tensiuni remanente .

La asamblarea prin sudare a doua table , din cauza aportului mare de caldura, concentrata intr-o zona restransa , se produc dilatari. Dupa racire, metalul depus se contracta antrenand si metalul de baza din vecinatate.

Deformatiile care apar , sunt insotite si de o stare tensionala de tensiuni remanente . Daca grosimea tablelor este suficient de mica, se pot neglija tensiunile perpendiculare pe planul acestora , ramanand tensiunile in lungul cusaturii-- si cele perpendicular pe cusatura - -Aceste tensiuni , sunt in echilibru, deoarece nu sunt generate de forta exterioara .

5.2.8.2. Masuri pentru combaterea deformatiilor si tensiunilor remanente

Pentru ca piesa sa fie folosita in bune conditii in urma operatiei de sudare, deformatiile si tensiunile trebuiesc inlaturate , intr-o masura cat mai mare.

Se prezinta cateva masuri ce au ca efect mentinerea deformatiilor si tensiunilor remanente la valori relativ mici, nesuparatoare.

-succesiunea corecta a executarii cusaturilor.

Elementele ce se sudeaza se recomanda sa fie asezate astfel incat, deplasarea acestora in timpul incalzirii si racirii sa se faca liber. Astfel , in cazul cusaturilor cap la cap, tablele se vor aseza ca in fig . 5.17.

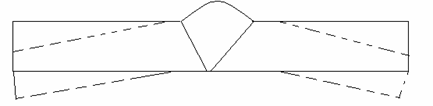
Fig 5.17

-Deformarea in sens opus.

Pentru ca piesele ce se sudeaza sa revina la forma initiala , acestea primesc o deformatie initiala corespunzatoare , de sens contrar , care se obtine mecanic, cu ajutorul unor dispozitive ca cel din figura 5.18. , sau prin incalzire cu flacara.

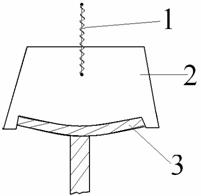
1.-Ghiare de deformare;

2.-Surub de actionare;

3.-Piesa de deformat;

Fig. 5.18

-Fixarea rigida a pieselor ce se imbina.

Fixarea in dispozitive este folosita pentru impiedicarea deformatiilor la sudarea in serie mare .

Dupa racire , piesele isi pastreaza forma, dar raman cu tensiuni remanente de valori mari. Acestea se diminueaza cu unul din procedeele prezentate in continuare:

-Preincalzirea ;

Determinarea temperaturii de preincalzire a pieselor ce se sudeaza se face, de regula, in functie de continutul de carbon.

-Detensionarea.

Detensionarea se recomanda cu precadere la sudarea otelurilor aliate sau a otelurilor carbon de dimensiuni mari .

Diagrama de detensionare se prezinta in fig. 5.19.

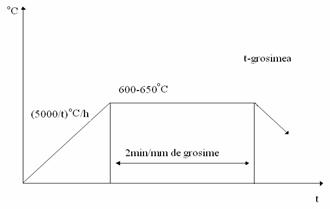
Fig. 5.19

5.2.9. Consideratii generale privind proiectarea constructiilor sudate

Proiectarea corecta a constructiilor sudate solicita, pe de o parte stapanirea tuturor parametrilor procedeelor de sudare, iar pe de alta parte, acceptarea ca metoda de realizare a pieselor si a sudurii, pe langa procedeele clasice (turnare, forjare, matritare, etc.)

Principiul de baza, care guverneaza dimensionarea asamblarilor sudate, este principiul de egala rezistenta.

Se prezinta in continuare si alte principii ce stau la baza proiectarii constructiilor sudate .

-asigurarea continuitatii fluxului liniilor de forte prin alegerea unei forme adecvate a pieselor;

-marirea rigiditatii constructiilor sudate prin micsorarea lungimii libere a elementelor ;

-micsorarea tensiunilor datorate constructiei, si a efectului de crestatura;

-realizarea constructiilor simetrice, pentru a minimaliza tensiunile interne ;

-la cordoanele de sudura solicitate din exterior, sa nu existe grosimi sub 4 mm;

-constructia sudata sa fie asamblata din parti componente cat mai mari, pentru micsorarea numarului de cordoane.

5.2.9.1. Exemple contructive de imbinari sudate

In constructia de masini exista elemente realizate exclusiv prin sudare, cum ar fi: recipienti, grinzi, boghiuri, etc.

In fig. 5.20 se prezinta un arbore cotit realizat prin sudura.

In fig. 5.21 este prezentata o roata dintata realizata prin sudura.

In fig. 5.22 este prezentata o carcasa de reductor realizata prin sudura.

   

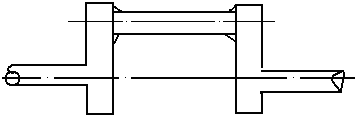
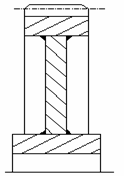
Fig. 5.20 Fig. 5.21

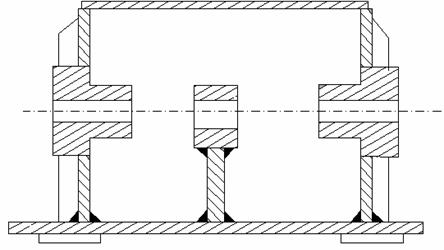Fig. 5.22

5.3. Asamblari nituite

5.3.1. Generalitati, descriere, clasificare

Nituirea face parte din categoria asamblarilor nedemontabile. Odata cu dezvoltarea procedeelor de sudare, nituirea si-a restrans aria de raspandire , in momentul de fata utilizandu-se:

- la piesele supuse la sarcini variabile, unde sudura este inca un procedeu nesigur ;

- piese din aliaje usoare din domeniul aviatiei;

- piese din materiale greu sudabile.

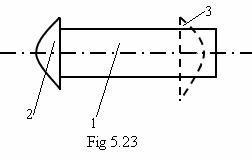Forma generala a unui nit este prezentata in fig.5.23. El se compune din:

- tija nitului -1

- capul fix -2

-capul de inchidere -3

Intre nit si piesele ce urmeaza a fi asamblate, se lasa un joc de diametru - j -

Formarea capului nitului, care se mai numeste si operatie de nituire, se poate face:

la rece - cand diametrele sunt de maxim 12 mm,

la cald - cand diametrul nitului depaseste 12mm

Din punct de vedere constructiv, exista mai multe solutii constructive atat pentru Formarea tijei cat si pentru cap.

Tija nitului poate fi plina - fig 5.22 sau tubulara. Aceasta se foloseste la diametre cuprinse in game 4 - 20 mm, si cu o grosime a peretelui de 0,25- 1,5 mm fiind foarte utilizate in aviatie, mecanica fina si industrie usoara.

Dupa Forma capului se intalnesc:

a)  cap semirotund - fig.5.2 a - sunt cele mai utilizate. Este usor de realizat, dar este voluminos si citeodata greu de amplasat in imbinare.

b)            cap inecat - fig.5.2b - necesita prelucrari suplimentare la piesele ce urmeaza a fi imbinate. Rezistenta capului este slaba in raport cu tija aceluiasi nit.

	a		b		c		d		e

Fig.5.2

c) cap plat - fig.5.2c - cu o gama restransa de utilizare - dogarie.

d) cap tronconic - fig.5.2 d - din punct de vedere al rezistentei corespund foarte bine, dar cu o tehnologie destul de greoaie.

e) cap semiinecat - fig.5.2e - imbina avantajul rezistentei nitului cu cap semirotund, cu avantajul ocuparii unui spatiu restrans al capului inecat.

f) cap tronconic si semiinecat - fig.5.2f - sunt utilizate ca nituri de rezistenta - etansare. Aduna dezavantajele de la ambele tipuri - cap tronconic si inecat.

g) nituri confectionate din teava - fig.5.2g - capul se formeaza prin altuire cu o raza de curbura mai mica sau mai mare.

Din punct de vedere al destinatiei , exista:

- Nituri de rezistenta. Acestea au capete semirotunde, tronconice, plate, semiinecate.

- Nituri de rezistenta - etansare pentru care se folosesc capete semirotunde, semiinecate, tronconice, tronconice si semiinecate

- Nituri de rezistenta si rezistenta - etansare se folosesc capete inecate.

Materiale folosite in realizarea niturilor, sunt:

otel carbon cu C<0,15%. in mod obisnuit OL34, OL37.

Cupru tras si recopt

Alama

Aluminiu

Duraluminiu

Otel aliat, in special cu Mo si Cr .

In anexa (A.5.2. tab.II ) se prezinta principalele dimensiuni ale niturilor din otel conform STAS

Imbinarile nituite se clasifica si ele, dupa destinatie, dupa cum urmeaza:

imbinari de rezistenta - se folosesc in constructia masinilor, a constructiilor metalice

imbinari de etansare - la rezervoarele deschise

imbinari de rezistenta si de etansare - se folosesc la realizarea cazanelor.

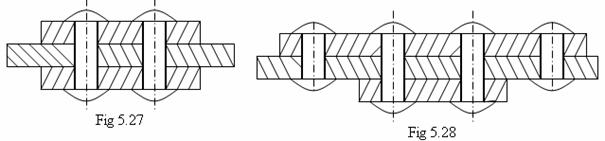
Imbinarile dupa modul de realizare pot fi:

directe - 5.25

cu eclipsa - fig.5.26

cu doua eclipse - fig 5.27 - simetrice, si fig. 5.28 - asimetrice.

5.3.2. Calculul imbinarilor nituite

Intr-o imbinare nituita directa tablele sunt solicitate la inconvoiere fig - 5.29

Dezaxarea fortei cu un brat egal cu grosimea tablei - s - ( fig.5.29.a ) produce un moment inconvoietor cu efect in curbarea tablelor ( fig.5.29.b).

In plus, in cazul nituirii la cald, racirea nitului produce o forat de tractiune in nit, care se poate calcula cu relatia : Fa =a . E . Dt .     (5.39)

In relatie :a - coeficient de dilatare liniara

E - modul de elasticitate

DT - diferenta de temperatura fata de mediul ambiant.

In aceste conditii Fa - strange piesele in capetele nitului, solicitarea intre table transmitandu-se cu ajutorul fortei de frecare. In metodologia calculului asamblarilor nituite, se fac urmatoarele ipoteze simplificatoare.

Niturile preiau o solicitare de forfecare.

Repartizarea solicitarii este uniforma in nit

Eforturile suplimentare se iau in consideratie doar cu coeficienti de reducere a rezistentelor admisibile.