REALIZAREA SI IMPLEMENTAREA LEGILOR TIPIZATE DE REGLARE

REALIZAREA SI IMPLEMENTAREA LEGILOR TIPIZATE DE REGLARE

Prezentare generala

In practica industriala a reglarii automate s-au impus asa numitele legi de reglare tipizate de tip PID (proportional - integrator - derivator) sau elemente de tip PID care satisfac majoritatea situatiilor cerintele tehnice impuse sistemelor de reglare conventionala. Se pot utiliza diverse combinatii ale celor trei componente: P = proportional; I = integrator; PI = proportional - integrator; D = derivator, ideal si real; PD = proportional - derivator ideal si real; PID = proportional - integrator - derivator, ideal si real in diferite variante.

Prin utilizarea acestor legi tipizate de reglare in cadrul unor reglatoare tipizate, proiectarea dimensional valorica a legii de reglare se reduce la alegerea tipului de lege si pozitionarea unor butoane prin care se prescriu valorile parametrilor acestor legi rezultate in urma proiectarii analitice a sistemului.

Nu se poate stabili precis efectul fiecarei componente a unei legi de tip PID asupra calitatii unui sistem de reglare automata, deoarece acestea depind de structura sistemului si de dinamica instalatiei automatizate.

Totusi se pot face urmatoarele precizari:

- componenta proportionala, exprimata prin factorul de proportionalitate K_r, determina o comanda proportionala cu eroarea sistemului. Cu cat factorul de proportionalitate este mai mare, cu atat precizia sistemului in regim stationar este mai buna dar se reduce rezerva de stabilitate putand conduce in anumite cazuri la pierderea stabilitatii sistemului.

- componenta integrala, exprimata prin constanta de timp de integrare T_i sau constanta de integrare echivalenta T_i^*, determina o comanda proportionala cu integrala erorii sistemului din care cauza, un regim stationar este posibil numai daca aceasta eroare este nula. Existenta unei componente I intr-o lege de reglare este un indiciu clar ca precizia sistemului in regim stationar (daca se poate obtine un astfel de regim) este infinita. In regim stationar, de cele mai multe ori componenta I determina cresterea oscilabilitatii raspunsului, adica reducerea rezervei de stabilitate.

componenta derivativa exprimata prin constata de timp de derivare T_d determina o comanda proportionala cu derivata erorii sistemului. Din aceasta cauza, componenta D realizeaza o anticipare a evolutiei erorii sistemului permitand realizarea unor corectii care reduc oscilabilitatea raspunsului. Aceasta componenta nu are nici un efect in regim stationar.

2. Forma discreta a legilor de tip PID

Dandu-se o lege continuala de tip PID se pune problema determinarii unui model pur discret care sa aproximeze in momentele de esantionare comportarea sistemelor continuale. Acesta este un caz particular al discretizarii proceselor continuale.

Principalele probleme sunt legate de aproximarea operatorilor de derivare si integrare. Operatorul de derivare se aproximeaza prin diferente in avans si prin diferente in intarziere, aproximari prezentate in continuare:

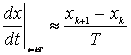- pentru aproximarea in avans

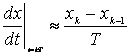- pentru aproximarea in intarziere.

Se recomanda utilizarea aproximarii derivatei cu diferente in intarziere. Operatorul de integrare se aproximeaza prin suma de dreptunghiuri sau de trapeze:

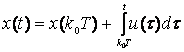
- aproximare prin suma de dreptunghiuri;

- aproximare prin suma de trapeze.

Aproximarea operatiei de integrare prin suma de trapeze este folosita in asa numita substitutie TUSTIN in care operatorul de integrare se poate aproxima prin operatorul discret

In metoda TUSTIN, considerand echivalarea de mai sus, operatorului s ii corespunde operatorul , rezultand functia de transfer discreta a unei functii continuale :

Exemplu: ;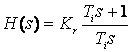

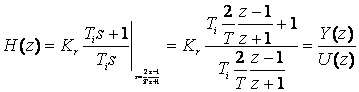
Folosind aproximarea derivatei prin diferenta inapoi si a operatorului de integrare prin suma de dreptunghiuri se obtine urmatoarea forma recursiva pentru o lege de tip PID:

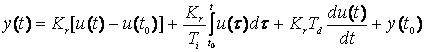
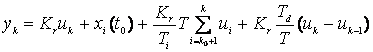
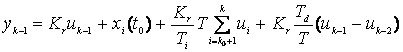
Se obtine urmatoarea ecuatie recursiva:

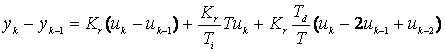
y_k = y_k-1+f(u_k,u_k-1,u_k-2).

In cazul utilizarii unei aproximari a integralei prin suma de trapeze se obtine urmatoarea ecuatie recursiva:

y_k = y_k-1+b₂u_k+b₁u_k-1+b₀u_k-2

unde

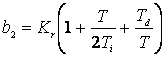
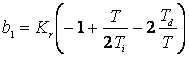
Implementarea algoritmilor tipizati

Lege de reglare de tip P

Printr-o lege de tip proportional se descrie comportarea intrare-iesire a unui element nedinamic (de tip scalar) sau comportarea in regim stationar a unui element dinamic, eventual descris printr-o functie de transfer H(s), considerand aceasta comportare liniara intr-un domeniu. Un element de tip P propriu-zis, este un element element nedinamic caracterizat prin urmatoarea functie de transfer :

H(s) = K_R ;

sau in prin relatia intrare-iesire:

y(t)=K_Ru(t).

K_R reprezinta factorul de proportionalitate sau factorul de amplificare de pozitie si se poate determina experimental prin raportul dintre variatia marimii de iesire in regim stationar si variatia marimii de intrare in regim stationar care a produs acea iesire. Din functia de transfer din domeniul Z se obtine ecuatia recursiva in domeniul timp:

In figura urmatoare sunt prezentate subsistemul SIMULINK pentru un element P si programul SIMULINK pentru afisarea raspunsului regulatorului la intrare treapta unitate.

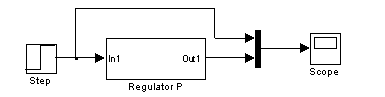
4.2. Lege de reglare de tip I

Functia de transfer a unui element de tip I este urmatoarea:

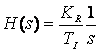
unde:     K_R - factorul de proportionalitate;

T_I - constanta de timp de integrare.

Relatia intrare iesire in domeniul timp este data de urmatoarea ecuatie diferentiala:

sau prin solutia :

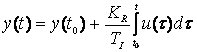, t > t₀

Functia de transfer se poate exprima printr-un singur parametru, constanta de timp echivalenta T_I^*,

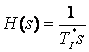, unde T_I^* =T_I/val

Folosind substitutia TUSTIN din H(s) obtinem:

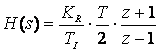, care ne conduce la urmatorea relatie de recurenta:

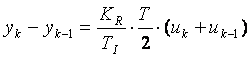
Implementarea sub SIMULINK a acestei ecuatii este urmatoarea:

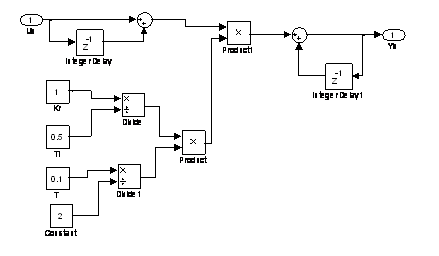
Programul SIMULINK pentru afisarea raspunsului regulatorului la intrare treapta unitate este urmatorul:

Modul de lucru:

Se vor implementa in SIMULINK cele doua tipuri de regulatoare prezentate mai sus si se vor obtine raspunsurile la semnale treapta.

Se va obtine forma discreta a regulatoarelor de tip PI, D (ideal si real), PD, (ideal si real) si PID (ideal si real) si se vor implementa in SIMULINK.