Operatori liniari pe spatii vectoriale

OPERATORI LINIARI PE SPATII VECTORIALE

Nucleul si imaginea unui operator liniar

Fie spatii vectoriale peste acelasi corp K.

Definitie   O functie se numeste operator liniar daca satisface:

Observatie Proprietatile 1 si 2 din definitie se pot inlocui cu:

Exemple:    1. operator identitate pe X
2. operatorul de derivare
3.

Propozitie Operatorul liniar are proprietatile:
a)
b)
c)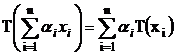

Notam L multimea operatorilor liniari din spatiul X in spatiul Y.

Pe aceasta multime  introducem operatiile:

- adunarea operatorilor (operatie bine definita, i.e. este operator liniar)

L L

- inmultirea operatorilor cu scalari (op bine def, i.e. este operator liniar)

L L

Observatie  (L) estespatiu vectorial peste corpul K.

- compunerea operatorilor (op bine def: U ○ T operator liniar)

- inversarea operatorilor (op bine definita: T^-1 operator liniar)
L, T functie bijectiva L a.i.

Definitie Se numeste nucleul operatorului liniar T, multimea notata:
 

Definitie Se numeste imaginea operatorului liniar T multimea notata:

Propozitie ker T este subspatiu vectorial al lui X, iar ImT este subspatiu liniar al lui U

Definitie Se numeste defectul lui T , dimensiunea subspatiului kerT, iar rangul lui T, dimensiunea subspatiului ImT

Propozitie , X spatiu de dimensiune finita

Matricea atasata unui operator, modificarea matricei unui operator la schimbarea bazelor.

Fie o baza in X, o baza in Y.

Fie cu coordonate in G :

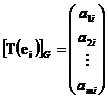
Definitie Matricea

se numeste matricea operatorului T in bazele E si G. Notam A sau A_T

Se obtine astfel o corespondenta intre mai precis un izomorfism

F:, 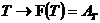si

Scrierea operatorului T cu ajutorul matricii atasate A_T

T

Adunarea operatorilor:

; E, G baze in X si Y ; matricile atasate.

, 

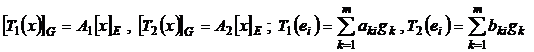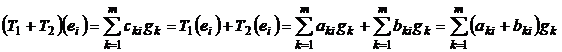
i.e.

Inmultirea operatorilor cu scalari:

,  aIK

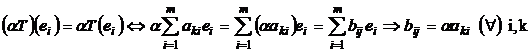
Modificarea matricii unui operator la schimbarea bazelor.

cu A matricea atasata in bazele E si G. In spatiul X trecem de la baza E la baza F

⁽¹⁾ unde

In spatiul Y trecem de la baza G la baza H: ⁽²⁾ unde

A = matricea atasata lui T in baza E si facem o schimbare de baza de la E la F.

Rezulta ca noua matrice atasata lui T in baza F este:

Vectori si valori proprii, diagonalizarea unui operator

Fie

Definitie Se numeste vector propriu al lui T, un vector x≠0 pentru care

( lIK a.i. T(x)=lx

l se numeste valoare proprie corespunzatoare vectorului propriu x.

Definitie Multimea se numeste subspatiu propriu corespunzator lui lIK

Propozitie X_l este subspatiu liniar al lui X , X_l X.

Algoritmul de determinare a valorilor si vectorilor proprii unui operator liniar sau matricii asociate lui.

Fie dimX=n si E= baza in X.

A_T=matricea operatorului T in baza E.

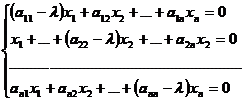este un sistem liniar omogen de ,,n" ecuatii cu,,n"necunoscute x_i , si admite solutii nenule det(A-lI)=0 care se numeste ecuatia caracteristica a operatorului T

Solutiile acestei ecuatii sunt valorile proprii ale operatorului T.

P(l)=det(A-lI) se numeste polinomul caracteristic lui T. Acesta e un polinom de grad ,,n" cu coeficienti in K , iar daca KsCTP(l) are ,,n" radacini(C este corp algebric inchis).

Propozitie Vectorii proprii corespunzatori la valori proprii distincte doua cate doua sunt liniar indepedenti.

Consecinta Daca operatorul T are n valori proprii distincte, atunci exista o baza in care matricea sa are forma diagonala si pe diagonala se gasesc valorile proprii.

Definitie  O matrice patratica are forma diagonala daca a_ij=0 ( ) i j

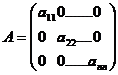
Definitie Un operator liniar este diagonalizabil daca exista o baza in care matricea sa are forma diagonala. Atunci o matrice patratica A este diagonalizabila daca exista o matrice C nesingulara, astfel incat  C^-1AC sa fie o matrice diagonala.