STUDIUL INTERFERENTEI PE LAME SUBTIRI INELELE LUI NEWTON

STUDIUL INTERFERENTEI PE LAME SUBTIRI

INELELE LUI NEWTON

Daca pe o lama transparenta cu fetele plan - paralele cade un fascicul de radiatii monocromatice, se constata ca o parte vor fi reflectate, iar o parte refractate. Intrucat undele incidente sunt paralele si undele reflectate vor fi paralele.

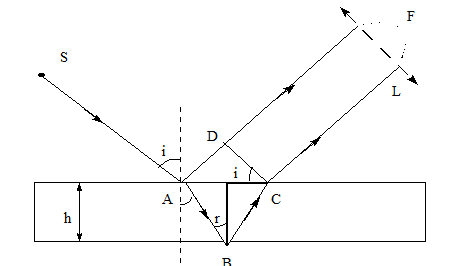
Pentru obtinerea interferentei in drumul razelor reflectate se aseaza o lentila convergenta L. In planul ei focal se vor obtine franje de interferenta. Se observa din figura ca intre unda reflectata in A pe prima fata si unda reflectata in B pe fata a doua, apare o diferenta de drum optic.

d = (AB + BC)n - AD + (1), unde n este indicele de refractie al lamei, se adauga deoarece prima unda se reflecta pe un mediu mai dens (aer - sticla). Din figura se observa ca AB = deci AB + BC = (2) unde h este grosimea lamei, iar r unghiul de refractie. Deasemenea

sin i = , AD = AC sin i (3)

Din D ABC => AC = 2 h tg r, pe care inlocuind-o in (3) obtinem

AD = 2 h tg r sin i = 2 h sin i (5)

Tinand seama de faptul ca sin i = h sin r, rezulta ca:

AD = 2 h n sin r =2 h n (6)

Inlocuind valorile obtinute la diferenta de drum optic rezulta:

d = (1 - sin² r) + = cos²r + deci d = 2 h n cos r +

Pentru d = 2 k obtinem maxime, iar pentru d = (2 k + 1) minime.

Intrucat sursele se gasesc la infinit, undele ce cad pe lama vor avea aceeasi inclinatie, adica vor avea aceeasi diferenta de faza. Franjele de maxim si minim corespund unei aceeasi inclinari a directiilor de propagare a razelor fata de fetele lamei, de aceea se numesc franje de egala inclinare. Franjele apar sub forma unor cercuri concentrice intunecate si luminate ce alterneaza intre ele, in planul focal al lentilei, numite inelele lui Heidinger. Daca observatia se face in lumina alba, in locul inelelor intunecate si luminate ce alterneaza intre ele, se obtin inele ce contin culorile spectrului. Daca lama este groasa nu obtinem franje de interferenta.

Interferenta in lame subtiri de grosime variabila. Franje de egala grosime

In figura de mai jos se considera doua lame de sticla ce fac un unghi intre ele realizand o pana de aer. Pentru fiecare grosime a lamei corespunzatoare se obtine o franja de interferenta. Franjele sun localizate pe fetele penei sau in spatiu cu ajutorul unei lentile convergente L.

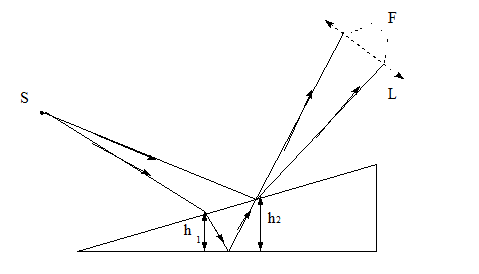
Astfel de franje se intalnesc des in practica. Un caz particular de franje de interferenta de egala grosime il constituie inelele lui Newton. Aceasta se realizeaza ca o pana de aer delimitata de a placa cu fetele plan-paralele si o lentila plan convexa asezata pe ea.

   

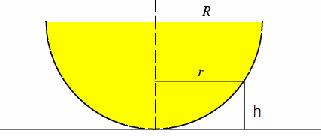
In cazul unei unde incidente normale si in aer, cos r = 1 si n = 1 ramane

d = 2 h +     (8)

care pentru maxim va fi 2 h + = 2 k (9)

de unde: 2 h = 2 k - = ( k - ) l (9')

Pe de alta parte, din figura precedenta rezulta : r_k² = R² ( R - h )h, unde neglijand pe h in comparatie cu R, h<R, rezulta: r_k² = 2 R h . (10)

Tinand seama de relatia (9) rezulta r_k² = ( k - ) l R ,    (11)

sau R = r_k² / ( k - ) l , (12)

unde : R este raza sferei din care face parte lentila;

k este ordinul maximului de interferenta;

r_k este raza inelului de ordin k;

l este lungimea de unda a radiatiei cu care se lucreaza.

Pentru a obtine raza inelelor minime se pune conditia de minim diferentei de drum optic de unde rezulta r_k² = k R l (13) , sau R = r_k² / k l (14)

Inelele se obtin in jurul punctului de contact dintre lentila si lama.

Aplicatii ale fenomenului de interferenta

Cu ajutorul fenomenului de interferenta se poate determina lungimea de unda a radiatiilor luminoase. Aceasta se realizeaza cu dispozitive optice in care apare o diferenta de drum intre undele luminoase, asa cum spre exemplu se intampla in cazul experientei lui Young, a oglinzilor Frasnel, dispozitivul ce realizeaza inilele lui Newton.

Se determina indicii de refractie, grosimi ale straturilor subtiri cu ajutorul interferentei fasciculelor multiple.

Pe baza interferentei in lame subtiri se poate verifica planeitatea unor suprafete,in special in atelierele de optica fina.

Franjele de egala grosime obtinute cu inele lui Newton au aplicatii la masurarea micilor deplasari sau deformari ale suprafetelor.

Pentru determinari se utilizeaza un microscop pe masute caruia se afla fixat dispozitivul pentru obtinere inelelor lui Newton, care poate fi deplasat in pozitia dorita cu ajutorul a doua cremaliere. In fata obiectivului este asezata o lamela din sticla P sub un unghi de 45^o fata de axa microscopului. Lumina de la o sursa monocromatica cade pe acesta lamela, care o reflecta pe dispozitiv. In campul vizual al microscopului se afla o scarita gradata care serveste la masurarea razeler inelelor.

Metoda de lucru

1. Se aprinde sursa de lumina monocromatica aranjandu-se in asa fel incat razele de lumina sa cada pe lamele de sticla P a microscopului si sa se reflecte vertical in jos, pe dispozitivul pentru obtinerea inelelor.

2. Se pune la punct microscopul ca sa se vada inelele cat mai clar, cu ajutorul surubului S.

3. Se masoara cu ajutorol micrometrului ocular diametrele inelelor de ordin k = 3,4,5,.. Cunoscand ca o diviziune mica a scaritei gradate reprezinta 0,0183 mm, se calculeaza raza inelului.

4. Cu ajutorul relatiilor (12) si (14) se determina raza de curbura a lentilei. Deoarece se foloseste lumina rosie se ia l = 7 10^-7 m.

5. Se vor face cel putin 5 determinari pentru minime si 5 determinari pentru maxime.