FIZICA FLUIDELOR

CARACTERISTICILE GENERALE

ALE FLUIDELOR

Prin fluid se intelege un mediu continuu, infinit divizibil, care isi modifica foarte mult forma sub actiunea unor forte mici. Din punctul de vedere al starilor de agregare ale substantelor, pot fi considerate fluide lichidele si gazele.

Un fluid se caracterizeaza prin anumiti parametri ce descriu starea lui in fiecare moment si anume densitatea r, presiunea p, campul de viteze ale diferitelor elemente de fluid, temperatura T. Un fluid este considerat un mediu continuu daca acesti parametri au valori bine determinate in fiecare punct al fluidului, la orice moment, fiind deci functii continue de punct si timp.

Densitatea unui fluid se defineste prin masa de fluid raportata la unitatea de volum. Daca fluidul considerat este omogen, avand masa m si volumul V, atunci prin definitie densitatea sa este data de expresia:

Unitatea de masura pentru densitate in Sistemul International este kg m^-3.

Daca fluidul este neomogen, formula (1.1) defineste densitatea medie a acestuia.

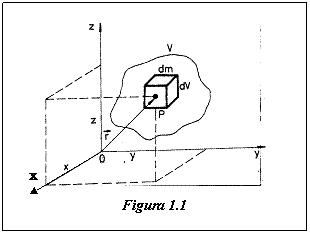
Pentru a defini densitatea fluidului intr-un punct dat, P, se considera un element de volum infinitezimal dV, (fig. 1.1.), situat in jurul punctului respectiv, a carui masa este dm. Densitatea in punctul P se va defini prin expresia:

Densitatea fiind un concept statistic, volumul dV trebuie sa fie suficient de mare pentru a contine un numar mare de molecule (si deci a avea o semnificatie fizica).

In general, densitatea unui fluid variaza de la punct la punct si de la un moment la altul, adica:

Se spune in acest caz ca functia descrie un camp de densitati.

Deoarece densitatea este o marime scalara, campul de densitati este un camp scalar.

Densitatea unui fluid depinde de temperatura si presiunea la care acesta este supus. In cazul lichidelor, densitatea variaza foarte putin cu presiunea si temperatura, astfel incat in multe situatii poate fi considerata constanta. In schimb, in cazul gazelor densitatea se modifica foarte mult la variatiile de presiune si temperatura.

Asupra unui fluid actioneaza forte ce pot fi exterioare sau interioare.

Fortele exterioare se datoresc unor cauze exterioare fluidului si pot fi de suprafata sau de volum.

Fortele exterioare de suprafata se datoresc unor corpuri exterioare care se afla in contact direct cu suprafata fluidului. Trebuie precizat ca exista o deosebire intre modul in care acestea actioneaza asupra unui lichid si asupra unui solid. In cazul unui solid nu exista nici o restrictie asupra directiei in care actioneaza forta, in timp ce pentru un fluid in repaus forta de suprafata trebuie sa fie intotdeauna orientata perpendicular pe suprafata.

Fortele exterioare de volum sunt fortele ce actioneaza asupra intregului volum de fluid prin intermediul unui camp fizic. Exemple pot fi actiunea campului gravitational asupra unui fluid, sau actiunea unui camp electromagnetic asupra unui fluid incarcat electric.

Fortele interioare se datoresc interactiunilor dintre diferitele elemente de volum din fluidul respectiv.

Daca aceste interactiuni se realizeaza prin contactul direct dintre elementele de fluid atunci fortele interioare respective se numesc de suprafata, iar daca ele se realizeaza prin intermediul unui camp fizic, fortele corespunzatoare se numesc interioare de volum.

In cazul fluidelor actiunea unei forte exterioare este descrisa prin presiunea p.

Prin definitie, presiunea reprezinta marimea fizica egala cu forta ce actioneaza normal pe unitatea de suprafata a fluidului:

Unitatea de masura in S.I. este N/m².

Daca forta F difera de la un punct la altul al suprafetei fluidului, atunci formula (1.4) defineste valoarea medie a presiunii.

Pentru a defini presiunea intr-un punct P al suprafetei, vom considera o suprafata inchisa (S) ce contine un fluid si pe ea un element de suprafata dS, centrat in punctul P. (fig.1.2).

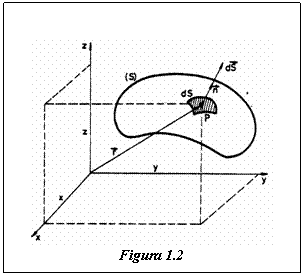
Elementul de suprafata dS poate fi reprezentat printr-un vector , de marime egala numeric cu aria sa si orientat dupa normala exterioara la suprafata in punctul P. Fie dF forta ce actioneaza normal la suprafata.

Presiunea in punctul P considerat, se defineste prin relatia:

Deoarece presiunea p poate varia de la un punct la altul al fluidului precum si de la un moment la altul, adica:

functia descrie un camp de presiuni, care este un camp scalar.

In cazul in care fluidul este in miscare, este necesar sa se introduca un camp de viteze corespunzator. Se defineste viteza fluidului intr-un punct P (fig.1.1) ca fiind viteza momentana a centrului de masa al elementului de volum dV ce inconjoara punctul P. Viteza fluidului poate, in general, sa difere de la punct la punct si de la un moment la altul, adica:

Se spune ca functia descrie campul de viteze al fluidului, care este un camp vectorial.

Daca un fluid are proprietatea ca nu-si modifica densitatea cand este supus actiunii unor forte exterioare atunci el se numeste incompresibil.

Daca densitatea se modifica sub actiunea fortelor exterioare, atunci fluidul se numeste compresibil. Lichidele sunt incompresibile, pe cand gazele sunt foarte compresibile.

Compresibilitatea unui fluid la temperatura constanta se caracterizeaza prin coeficientul de compresibilitate, l, sau prin inversul acestuia numit modulul de compresibilitate.

Coeficientul de compresibilitate este definit ca variatia unitatii de volum de fluid pentru o crestere a presiunii egala cu unitatea.

(1.8)

unde V este volumul initial, iar dV variatia de volum datorita cresterii presiunii cu dp. Semnul minus se datoreste faptului ca o crestere de presiune conduce la o micsorare de volum.

Unitatea de masura pentru coeficientul de compresibilitate in Sistemul International este N^-1m². l este, practic, constant pentru lichide, in intervale mari de variatie a presiunii.

La presiunea si temperatura obisnuita l 10^-10N^-1m² pentru apa si l 10^-11N^-1m² pentru mercur. Pentru majoritatea lichidelor, l creste odata cu temperatura, iar pentru apa scade cand creste temperatura. Avand coeficienti de compresibilitate atat de mici, lichidele pot fi considerate, practic, incompresibile.

In cazul gazelor perfecte se poate determina coeficientul de compre-sibilitate izoterma utilizand legea lui Boyle si Mariotte,

Diferentiind relatia (1.9.) se obtine:

adica

Coeficientul de compresibilitate izoterma pentru un gaz perfect este, deci, egal cu inversul presiunii gazului, iar modulul de compresibilitate izoterma este egal cu presiunea. Pentru un gaz perfect la presiunea ordinara, l=10^-5 N^-1m², deci un gaz perfect este de 20 000 de ori mai compresibil decat apa.

O alta caracteristica importanta a fluidelor o constituie vascozitatea.

Aceasta reprezinta proprietatea fluidului de a se opune la alunecarea unui strat de fluid fata de straturile vecine. Vascozitatea este caracterizata prin aparitia in fluidul respectiv a unor forte tangentiale de interactiune intre straturile vecine, numite forte de frecare interne.

Un fluid care prezinta proprietatea de vascozitate se numeste fluid vascos. Fluidele vascoase sunt gazele reale si lichidele. Vascozitatea lor este determinata de miscarea moleculelor componente. Astfel moleculele dintr-o regiune aflata in miscare cu o viteza mare se ciocnesc cu moleculele regiunii vecine ce se misca cu o viteza mai mica, determinand un transfer de impuls de la prima regiune catre cea de-a doua. Acest transfer de impuls sta la originea vascozitatii fluidului. Miscarea moleculelor fiind afectata de temperatura mediului, rezulta ca si vascozitatea este, de asemenea, dependenta de temperatura.

Fluidele care nu prezinta proprietatea de vascozitate se numesc ideale.

Sunt fluide ideale gazele foarte rarefiate si lichidele in miscare cu viteza foarte mica.

Astfel de fluide nu exista in natura, studiul lor este important din punct de vedere teoretic, ca o prima aproximatie a fluidelor reale.

1.2 STATICA FLUIDELOR

1.2.1 LEGEA FUNDAMENTALA A STATICII

FLUIDELOR

In cadrul staticii fluidelor se studiaza proprietatile fluidelor aflate in stare de repaus. Un fluid se considera in stare de repaus daca orice element de volum din structura sa are la orice moment o viteza nula, adica are un camp de viteze nul. Campul de presiune va fi in acest caz o functie de punctul considerat, adica .

Daca fluidul este ideal si se afla in repaus, atunci intre diferitele sale straturi nu pot apare forte tangentiale de interactiune. Prezenta unor asemenea forte ar contribui la deplasari ale straturilor de fluid, si deci fluidul nu ar mai fi in repaus. Prin urmare, in cazul fluidelor ideale aflate in repaus singurele forte care apar sunt cele normale numite forte de presiune.

Problema fundamentala a staticii fluidelor o constituie obtinerea unei legi care sa permita determinarea campului de presiune in interiorul unui fluid aflat in repaus.

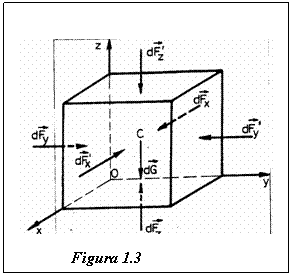
Sa consideram un element de volum infinitezimal in fluidul aflat in echilibru, de masa dm si avand forma unui paralelipiped cu laturile dx, dy, dz (fig.1.3.).

Vom presupune ca singura forta exterioara de volum care actioneaza asupra fluidului este determinata de campul gravitational. Ea are expresia:

unde reprezinta vectorul acceleratiei gravitationale.

Deoarece:

si dV=dxdydz expresia (1.12) devine:

unde r(x,y,z) reprezinta densitatea fluidului in centrul C al elementului de volum dV.

Actiunea restului fluidului asupra acestui element de volum poate fi inlocuita prin forte , normale pe fetele lui si indreptate spre interiorul lui.

La echilibru, putem scrie de exemplu pentru fetele perpendiculare pe Ox:

deci p = p'

unde p este presiunea pe fata elementului de volum continuta in planul yOz si p' presiunea pe fata paralela cu ea.

Un rezultat asemanator se obtine scriind conditia de echilibru pentru fetele perpendiculare pe axa Oy.

deci p = p'

Valoarea presiunii este, deci, aceeasi pentru o valoare data a lui z, oriunde s-ar afla suprafata pe care ea se exercita, deci presiunea este aceeasi in toate punctele unui plan orizontal.

Sa scriem conditia de echilibru in cazul fetelor perpendiculare pe directia Oz:

unde dp=p₁'-p₁

Relatia (1.19.) se mai poate scrie sub forma:

Expresia (1.20.) reprezinta legea fundamentala a staticii fluidelor scrisa pentru cazul cand singurele forte exterioare de volum ce actioneaza asupra fluidului sunt cele determinate de campul gravitational.

Daca se admite ca asupra elementului de fluid considerat actioneaza si alte forte exterioare de volum si se noteaza prin valoarea rezultanta a tuturor fortelor exterioare de volum, raportata la unitatea de masa a fluidului, atunci legea fundamentala a staticii fluidelor se va scrie sub forma generala:

PRESIUNEA HIDROSTATICA

Sa determinam distributia presiunii intr-un fluid incompresibil (r=const.), de exemplu un lichid aflat in repaus in campul gravitational (fig.1.4.).

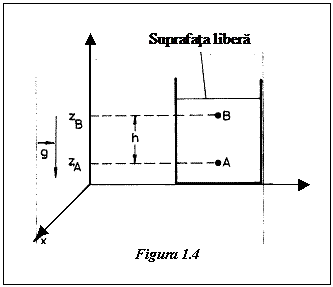
Legea fundamentala (1.20.) poate fi inlocuita in acest caz prin urmatoarele trei ecuatii scalare:

Gradientul presiunii care caracterizeaza variatia presiunii in spatiu si este dat de derivatele partiale ale acesteia, este un vector perpendicular pe suprafetele de presiune constanta (in sensul cresterii

presiunii), deci este perpendicular pe suprafetele de camp gravitational constant in sensul acestui camp. In cazul de mai sus aceste suprafete sunt orizontale si campul este vertical in jos, de aceea gradientul presiunii s-a redus numai la componenta verticala. Ultima ecuatie din (1.22) se poate scrie atunci sub forma:

Fluidul fiind presupus incompresibil (r=const), ecuatia (1.23.) poate fi integrata intre limitele ce corespund, de exemplu, punctelor A si B:

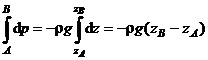sau

unde h este diferenta de nivel intre punctele B si A.

Expresia rgh este denumita presiune hidrostatica si reprezinta presiunea pe care o exercita in punctul A lichidul cuprins intre nivelele ce trec prin A si respectiv B.

Daca punctul B este chiar pe suprafata lichidului, atunci se noteaza p_B cu p₀, unde p₀ reprezinta presiunea atmosferica. Considerand punctul A arbitrar ales ecuatia (1.24) devine:

(1.25)

unde h reprezinta adancimea la care se afla punctul in care se calculeaza presiunea p.

Daca campul de forte exterioare ce actioneaza asupra fluidului este conservativ, atunci forta de volum deriva dintr-un potential, in sensul ca poate fi scrisa sub forma U. Raportand aceasta forta la unitatea de masa se obtine:

U = - V

unde V = U/m reprezinta potentialul campului exterior.

Din relatiile (1.21) si (1.26) rezulta:

p V 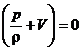, adica

Relatia (1.27) exprima faptul ca intr-un fluid incompresibil aflat in repaus intr-un camp exterior de forte conservative, suprafetele de presiune constanta sunt in acelasi timp si suprafete de potential constant, adica sunt suprafete echipotentiale.

In exemplul considerat suprafetele echipotentiale sunt plane orizontale.

Suprafata lichidului, numita suprafata libera, este de asemenea o suprafata echipotentiala. Pe aceasta proprietate se bazeaza principiul vaselor comunicante, conform caruia nivelul unui lichid turnat in doua vase ce comunica intre ele este acelasi in ambele vase.

1.2.3. FORMULA BAROMETRICA

O aplicatie a legii fundamentale a staticii fluidelor o constituie deter-minarea campului de presiune intr-un fluid compresibil aflat in echilibru in campul gravitational al Pamantului, de exemplu atmosfera. Fluidul se caracterizeaza prin proprietatea ca densitatea sa intr-un punct oarecare este functie numai de presiunea din acel punct: r r(p). Astfel de fluide se numesc barotrope. Exemple de astfel de fluide sunt gazele ideale, apa marilor si oceanelor, atmosfera Pamantului.

Legea fundamentala a staticii fluidelor se scrie pentru fluidele barotrope, astfel:

Prin integrare rezulta:

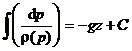
unde C este o constanta de integrare ce se determina din conditii la limita.

Se alege o forma particulara pentru functia r(p) cu scopul de a evalua analitic sau numeric integrala din membrul stang al relatiei (1.29). Se considera ca fluid barotrop gazul ideal. Se utilizeaza ecuatia de stare a gazului ideal:

din care se poate exprima densitatea:

Inlocuind (1.31) in (1.29) si integrand rezulta:

Daca se admite conditia la limita p=p₀ pentru z=0, rezulta .

Relatia (1.32) devine:

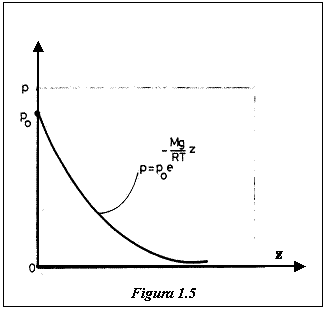
Relatia (1.33) constituie formula barometrica si arata ca in cazul fluidelor compresibile barotrope, aflate in camp extern gravitational si care se supun legii gazelor perfecte, presiunea scade exponential cu inaltimea (fig. 1.5.).

Cercetarile experimentale au pus in evidenta faptul ca atmosfera Pamantului poate fi considerata ca un fluid barotropic pentru care este valabila formula barometrica. Pentru ea, nivelul z=0 se alege nivelul marii.

1.3 DINAMICA FLUIDELOR

1.3.1 CURGEREA FLUIDELOR.

ECUATIA DE CONTINUITATE

Pentru descrierea miscarii unui fluid se adopta metoda dezvoltata de L. Euler, conform careia se cunosc in fiecare moment si in fiecare punct al fluidului valorile urmatorilor parametri: viteza , densitatea r, presiunea p.

Curgerea unui fluid poate fi considerata:

- stationara, daca viteza a fluidului in fiecare punct este constanta. Prin urmare, intr-un punct dat al fluidului, viteza oricarui element de fluid ce trece prin el este totdeauna aceeasi.

- nestationara, daca viteza fluidului intr-un punct dat depinde de timp.

Curgerea unui lichid printr-o conducta prezinta doua tipuri limita de regimuri de curgere:

- curgerea laminara in care elementele de volum de fluid se misca regulat si paralel.

- turbulenta, caracterizata printr-o variatie a vitezelor in mod neregulat de la punct la punct si de la un moment la altul. Turbioanele sunt dispuse dezordonat fata de directia generala de curgere si liniile de curent sunt asezate neregulat unele fata de celelalte.

Curgerea unui fluid poate fi compresibila sau incompresibila dupa cum fluidul considerat este compresibil sau nu.

Analog, curgerea poate fi vascoasa sau nevascoasa dupa cum fluidul este vascos sau ideal.

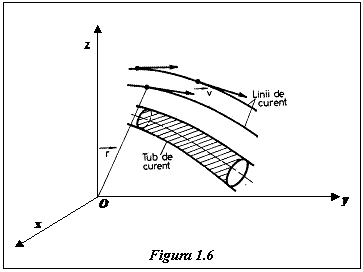
Se defineste linia de curent ca fiind traiectoria descrisa de un element de fluid in miscarea sa (Fig.1.6.).

O linie de curent se caracterizeaza prin aceea ca vectorul viteza al elementului de fluid este tangent la linie in fiecare punct al sau.

In cazul unei curgeri stationare liniile de curent nu se pot intersecta intre ele.

Totalitatea liniilor de curent care trec printr-un contur inchis formeaza un tub de curent (Fig.1.6.). Intr-o curgere stationara liniile de curent din

interiorul unui tub de curent nu pot parasi tubul.

Fluidul care intra la un capat al tubului trebuie sa iasa prin celalalt capat.

O marime caracteristica unui fluid aflat in miscare o constituie debitul volumic Q_v, al acestuia.

Prin definitie, debitul volumic printr-o suprafata data reprezinta mari-mea fizica numeric egala cu un volum de fluid ce trece in unitatea de timp prin acea suprafata.

Unitatea de masura in S. I. este m³/s.

Daca debitul volumic variaza de la un moment la altul prin suprafata considerata, relatia (1.34.) defineste valoarea medie a debitului in timpul t. Pentru a defini valoarea momentana a debitului volumic, se considera un interval de timp infinitezimal dt si se noteaza cu dV volumul de fluid ce trece in acest interval prin suprafata considerata. Debitul volumic se poate defini atunci prin relatia:

Se defineste debitul masic Q_m, al fluidului printr-o suprafata data, ca fiind marimea fizica egala cu masa de fluid ce trece in unitatea de timp prin suprafata respectiva.

Unitatea de masura in S. I. este kg/s.

Aplicand relatia de definitie a densitatii

rezulta urmatoarea relatie de legatura intre cele doua marimi Q_v si Q_m.

Ecuatia de continuitate care constituie una dintre ecuatiile fundamentale din dinamica fluidelor exprima de fapt legea conservarii masei de fluid.

Vectorul

se numeste vectorul densitatii fluxului de masa. Directia sa coincide cu cea a miscarii fluidului, iar marimea sa determina cantitatea de fluid care trece in unitatea de timp prin unitatea de suprafata dispusa normal la directia de miscare.

1.3.2 ECUATIA DE MISCARE A LUI EULER

Problema fundamentala urmarita in curgerea fluidelor adica in dinamica fluidelor o constituie determinarea campului de presiune si a campului de viteze ale unui fluid aflat in miscare.

Aceste marimi sunt determinate de ecuatia lui Euler, care este ecuatia de miscare a unui fluid.

Pentru a deduce aceasta ecuatie se va considera un element de volum infinitezimal din fluidul aflat in miscare, de masa dm si avand forma unui paralelipiped cu laturile dx, dy, dz. Asupra fluidului pot actiona forte de suprafata si forte volumice.

Forta de suprafata rezultanta, care actioneaza asupra intregului element de volum considerat, va fi deci:

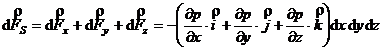
sau

unde p este gradientul campului de presiune p(x,y,z), adica:

Asupra acestui element de fluid se exercita si o forta volumica a carei valoare raportata la unitatea de masa se noteaza cu . Forta de volum ce actioneaza asupra elementului de fluid dV se va exprima prin relatia:

Forta rezultanta ce actioneaza asupra elementului de fluid considerat are expresia:

Aceasta forta determina o miscare accelerata a fluidului in conformitate cu legea a doua a lui Newton:

unde si

Din expresiile (1.43.) si (1.44.) se obtine:

Deoarece elementul de volum dV = dxdydz este arbitrar ales:

Expresia (1.46) reprezinta ecuatia de miscare a lui Euler pentru un fluid ideal, scrisa sub forma vectoriala.

Aceasta ecuatie, impreuna cu ecuatia de continuitate si conditiile initiale si de marginire corespunzatoare, determina complet campul de viteze si campul de presiune , daca se presupune ca fluidul este incompresibil (r =const.) si se cunoaste forta de volum raportata la unitatea de masa, .

In cazul unui fluid compresibil este utila o relatie termodinamica pentru densitate, de exemplu de forma r r(p) ca in cazul fluidelor barotrope.

In cazul unui fluid in repaus , deci in absenta oricarei forte externe, rezulta:

p

deci p = const. pentru orice punct din masa fluidului.

Daca asupra fluidului in repaus singura forta exterioara de volum care actioneaza este aceea determinata de campul gravitational , expresia (1.46.) devine:

deci

adica regasim legea fundamentala a staticii fluidelor.

In cazul unei curgeri stationare, deci cand intr-un punct din masa fluidu-lui viteza nu depinde de timp , si ecuatia lui Euler (1.73.) devine:

1.3.3 ECUATIA LUI BERNOULLI

Sa consideram miscarea unui fluid ideal si incompresibil printr-un tub de curent (sau conducta), presupunand ca singura forta exterioara de volum ce actioneaza asupra sa este aceea datorata campului gravitational.

Asupra unui element de volum actioneaza forta de volum de greutate , care raportata la unitatea de masa are expresia:

are componentele g_x g_y g_z=-g Prin inlocuirea expresiei (1.50.) in ecuatia de miscare a lui Euler (1.46.), se obtine pe componente:

, ,

Inmultind prima din ecuatiile (1.51.) cu dx, a doua cu dy si a treia cu dz si insumandu-le membru cu membru, rezulta:

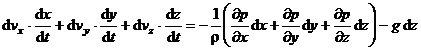sau

Deoarece v =v_x +v_y +v_z prin diferentiere se obtine d(v²)=2(v_xdv_x+

v_ydv_y+v_zdv_z) Ecuatia (1.52.) se mai poate scrie sub forma:

Tinand seama ca fluidul este incompresibil (r=const) si g=const, ecu-atia (1.53.) se scrie:

De aici, rezulta:

care exprima legea lui Daniel Bernoulli pentru un fluid ideal, incompresibil care se misca in camp gravitational.

Termenul rv se numeste presiune dinamica a fluidului, termenul rgz este presiunea hidrostatica, iar p se numeste presiune statica. Legea lui Bernoulli se poate enunta astfel:

Intr-o curgere stationara a unui fluid ideal, incompresibil, aflat in camp gravitational, suma dintre presiunea dinamica, hidrostatica si statica ramane constanta de-a lungul unei linii de curent.