Parametri ai educatiei intre deziderat si realizare

Parametri ai educatiei intre deziderat si realizare

Trebuie sa recunosc ca, la prima vedere, tema propusa pentru acest referat a parut complicata. in timp, gandindu-ma, am ajuns la concluzia ca, de fapt, trebuie sa discutam despre ceea ce dorim sa realizam si ceea ce realizam in cadrul orelor de matematica.

Pornind de la ideea ca :"Educatia este o cultura a caracterului, o obisnuinta contra naturii, dar si singura care-i distinge pe oameni, este o arta, care face sa treaca constientul in subconstient, este un fapt al scolii, si al unei virtuti, pe care o porti cu tine.", putem spune ca noi , dascalii incercam din rasputeri ca procesul educativ sa se realizeze cat mai bine. Este stiut ca sistemul educativ este "competent" in dependenta de mediul inconjurator, practicile educative invatate de parinti, comportamentul fata de scoala, practicile sociale asimilate din institutiile scolare. A invata nu este pur si simplu un proces psihologic si biologic, si nu face diferentiere de persoanele din diferite paturi sociale. invatarea este un proces continuu, care este determinat de relatiile sociale de productie.

in prezent, aptitudinile si capacitatile unei persoane au o mai mare importanta decit asimilarea unei cantitati mari de cunostinte, care nu aduc nici un rod societatii. Acest adevar incontestabil trebuie luat in considerare de cei care intocmesc programele scolare si chiar manualele scolare.

Imediat dupa decembrie 1989, cei care se ocupa de destinele matematicii in tara noastra s-au trezit asaltati de intrebari. Ce fel de matematica facem noi romanii? Este ea utila noilor cerinte impuse de viata; se adapteaza ea economiei de piata? Si daca nu, care capitole trebuie 'restructurate'? Daca reforma invatamantului este iminenta, in cadrul acesteia este oare necesara si reforma invatamantului matematic?

Urmand regula generala a tranzitiei catre economia de piata, in Romania, matematicienii s-au divizat imediat in conservatori si reformisti, aducand ca si in domeniul economic sau politic argumente pro si contra.

Sa imaginam un dialog al controverselor celor mai frecvente:

-la olimpiadele de matematica internationale, elevii nostri ocupa intotdeauna locuri fruntase (argument conservator 'forte' des intalnit).

-este adevarat, riposteaza reformistii, dar acestia reprezinta o foarte mica minoritate care este instruita special in taberele de matematica. Apoi olimpicii nostri sunt 'dopati' in particular de meditatori si nu reprezinta marea masa a elevilor care abia se descurca in problemele claselor invatamantului obligatoriu.

-dar faptul ca obtin premii inseamna ca avem profesori buni.

-avem dar neorganizati, singulari, fara un cadru adecvat de cercetare. Apoi dupa desfiintarea Institutului de Cercetare Matematica in 1971 de catre Ceausescu, 'crema' matematicii noastre a emigrat in marile orase din vest.

-programa noastra de matematica este net superioara : capitole mai multe, bogate, probleme variate.

romanii spuneau, 'non multa, sed multum' - nu multe, ci mult. Abundenta notiunilor matematice ce se cer invatate este mai degraba o pierdere de timp pentru teoretic in defavoarea nevoii practice. Cati din absolventii scolii generale aplica aceste notiuni in practica? Chiar a imparti o coala de tabla in figuri geometrice simple, cu o anumita arie, este o dificultate pentru ei.

-suntem in era microelectronicii si astfel de probleme simple nici nu se mai pun. Calculatoarele fac totul

-atunci sa nu mai invatam in scoala generala extragerea radicalului, sau in scoala primara inmultirea pentru ca orice calculator de buzunar are tastele 'radical' sau 'inmultit' ?

Si dialogul controverselor ar putea continua la infinit.

Se poate da un raspuns transant?

intregul sistem de educatie matematica se confrunta cu un mare esec. La noi nu se dezvolta placerea de a invata matematica, iar de vina sunt programele scolare, manualele, si uneori si noi,cei care predam la clasa. Exista in randul elevilor o mare discrepanta intre aspectul de corectitudine si cel de a intelege. Se poate sa se rezolve ceva corect, dar fara a se intelege', a spus academicianul Solomon Marcus in cadrul unei dezbateri organizate la Comisia Nationala a Romaniei pentru UNESCO. La dezbaterea intitulata 'Cui ii e frica de matematica?' au participat patru generatii de olimpici, de la cei mai tineri, care se pregatesc pentru barajele olimpiadelor internationale si pana la fostii olimpici, deveniti profesori de prestigiu. Olimpicii mai tineri au spus ca profesorul din gimnaziu a fost principalul 'vinovat' pentru ca s-au indragostit de matematica, iar cei mai in varsta au afirmat ca frica de matematica este inventata de societate.

Un lucru e cert matematica trebuie predata intr-un mod cat mai apropiat de varsta si preocuparile elevilor si tematica sa fie cat mai atractiva.Poate asa nu vom mai fi pusi in situatia sa predam teorema lui Pitagora unor elevi care nu cunosc ridicarea la putere sau teorema lui Thales fara a sti ce este acela un raport.

In continuarea referatului mi-am permis sa adaug cateva mijloace moderne, participativ- active de invatare     a principalelor notiuni matematice

PREZENTAREA PROBLEMEI:

Daca principalele operatii aritmetice:, ", ,,-" , ,,:",,,*''sunt relative usor de asi-

milat de catre elevii claselor primare cu un QI suficient de mare,incepand din clasa a V-a exista anumite ,,trepte " in invatare pe care elevii pot sau nu sa le depasesca.

De depasirea acestor ,,trepte" depinde succesul in abordarea celorlalte notiuni de matematica.

in cele ce urmeaza vom prezenta cateva momente dificile si esentiale ale trase-

ului matematic la elevi cat si metode moderne si eficiente de asimilare a competen-

telor respective.

,,TREAPTA 1" ADUNAREA FRACtIILOR

avand in vedere ca majoritatea elevilor cu aptitudini pentru matematica nu accepta sa retina si sa aplice diversi algoritmi fara o motivare prealabila vom prezenta o varianta de deducere problematizanta a algoritmului de adunare a fractiilor.

Pas 1: Se vor aminti urmatoarele:

• O fractie este definita de doua numere:numarator si numitor

Ex.1) se citeste trei cincimi(adica 3 ne arata cate cincimi sunt,le innumara,de aceea se numeste numarator,iar 5 ne arata ca avem de-a face cu cincimi

(denumeste tipul de fractie) deoarece se numeste numitor (ne arata cum le cheama pe fractii)

Ex.2) se citeste sapte optimi-7 ne arata numarul lor (numarator) si 8 ne arata numele lor (numitor)

• a) O fractie are o semnificatie care porneste chiar din citirea sa.De exemplu =trei cincimi inseamna ca impartim intregul in cinci (cincimi) si alegem trei din cele 5 cincimi.

b) O fractie are si o semnificatie algebrica(numerica). De exemplu =0

• avand in vedere observatiile anterioare ,prin doua- trei exemple se motivea-

za grafic si algebric metoda de obtinere a fractiilor echivalente prin amplificare si simplificare.

Pas 2: Se va propune elevilor efectuarea grafica sau eventual algebric a urmatoarelor adunari:

   

   

   

Pentru o adunare rapida a fost necesara amplificarea fractiilor in scopul aducerii la acelasi numitor,numitorul comun fiind un multiplu comun al numitorilor fractiilor care se aduna.

In final,elevii vor intelege ca aducerea fractiilor la acelasi numitor in scopul adunarii sau scaderii se efectueaza nu de dragul unui algoritm ci pentru ca fractiile trebuie sa fie toate ,,de acelasi tip", adica sa fie toate cu acelasi numitor pentru a opera doar cu numaratorii.

2.metode ,,mentale" de retinere si deducere a formule-

lor de calcul prescurtat(descoperirea problematizanta a triunghiului lui pascal,chiar la clasele gimnaziale)

daca vrem sa exprimam (a+b)² ne imaginam doar ca desfiintam parantezele (a+b)(a+b) la care se cor obtine termini de tipul a² ab b².La a² si la b² avem

o singura varianta dar la ab avem doua variante: ,,a'' din prima paranteza si

,,b ''din a doua paranteza si invers.De aceea ab are coeficientul 2.Deci, (a+b)²=1a²+2ab+1b².

Este recomandabil ca elevii sa revina la aceste idei insistent,pana le asimileaza,decat sa invete mechanic formula (a+b)²

Acelasi mecanism se recomanda a fi aplicat si pentru deducerea mentala a formulei (a+b)³=(a+b)(a+b)(a+b).Prin desfasurare se obtin termeni de tipul:

a³ cand din fiecare din cele trei paranteze luam pe a

a²b cand din doua paranteze luam pe a si din a treia pe b

ab² cand dintr-o singura paranteza luam pe a si din celelalte doua pe b

b³ cand din fiecare din cele trei paranteze luam pe b

Ne intrebam ce coeficienti au termenii de mai sus?

a³ are coeficientul 1 deoarece avem o singura varianta in care luam din toate cele trei paranteze pe a

a²b apare cand luam pe a din: I -p₁ si p₂

II- p₁ si p₃

III- p₃ si p₂

Deci, a²b are coeficientul 3 .Analog si la coeficientii lui ab² si b³.

Rezulta ,mental , ca (a+b)³ =1a³+3a²b +3ab²+b³

Un mecanism asemanator se va aplica si pentru deducerea lui (a+b)⁴

Se va observa ca pentru deducerea lui (a+b)⁵ sau puteri mai mari,calculul anumitor coeficienti poate necesita un timp suficient de mare. Spre ex.la (a+b)⁵ coeficientul lui a³b²coincide cu numarul de variante(posibilitati) de a alege trei paranteze din cinci.(pentru ca s-a luat a din 3 paranteze si b din 2 paranteze)obtinand variante de tipul p₁ p₂ p_3, p₁ p₂ p₄, p₁ p₂ p₅ etc.,astfel incat se pune natural problema sa putem deduce pe (a+b)⁴ din (a+b)³ sau pe (a+b)⁵ din (a+b)⁴ etc, mai ales daca avem in vedere mecanismul recurential de percepere al puterilor.

Ex. 2¹¹=2¹⁰2 ; 2¹⁰³=2¹⁰²2

Scriind (a+b)⁴ =(a+b)³(a+b),termenul a³b din dezvoltarea (a+b)⁴ se obtine din termenul a²b al dezvoltarii (a+b)³ prin inmultire cu a sau din termenul a³ al dezvoltarii (a+b)³ prin inmultire cu bcoeficientul lui a³b va fi suma coeficientilor lui a²b si a³ din dezvoltarea (a+b)³.Analog termenul a²b² din dezvoltarea (a+b)⁴ se obtine din termenul ab² al dezvoltarii (a+b)³ prin inmultire cu a si din termenul a²b al dezvoltarii (a+b)³ prin inmultire cu bcoeficientul lui a²b²este suma coeficientilor lui a² b si ab² din dezvoltarea (a+b)³

Analog se constata ca suma coeficientilor termenilor a²b² si a³b din dezvoltarea (a+b)⁴ este coeficientul termenului a³b² al dezvoltarii (a+b)⁵,etc. efectuand

numai adunari putem deduce usor dezvoltarea (a+b)ⁿ pentru n=2,3,4 . ,10.

Recomandand elevilor sa scrie formulele (a+b)¹, (a+b)², (a+b)³,(a+b)⁴ deduse dupa prima metoda,simetric,una sub alta pentru a vedea daca se confirma constatarile anterioare,se regaseste de fapt triunghiul lui Pascal.

(a+b)¹= 1a+1b

(a+b)²= 1a²+2ab+1b²

(a+b)³= 1a³+3a²b+3ab²+1b³

(a+b)⁴=1a⁴+4a³b+6a²b²+4ab³+1b⁴

Astfel se vor putea deduce usor formulele pana la (a+b)¹⁰

OBS.Prima explicatie conform careia coeficientul lui a^n-kb^k din (a+b)ⁿ coincide cu numarul de posibilitati de a alege k paranteze din n paranteze conduce direct la formula binomului lui Newton cand este cunoscuta notiunea de combinari,astfel incat elevii nu trebuie sa mai memorize formula binomului lui Newton daca au primit in prealabil explicatii de tipul celor de mai sus.

prezentarea problematizanta a descoperirii formulei radicalilor compusi

avand in vedere ca in programa scolara la gimnaziu si la liceu calculele cu radicali si proprietatile radicalilor ocupa un spatiu suficient de mare am considerat oportun sa indicam o metoda de deducere a formulei radicalilor compusi pe care nu am gasit-o in nici un manual

Pas1:Se explica elevilor ca radicalii compusi ar fi niste expresii de forma:"radical din radical" adica: sau si ne-ar interesa sa putem simplifica expresiile care contin radicali compusi.

Pas 2:Se va da un exemplu simplu de astfel de simplificare

,pentru a-l simplifica trebuie sa scriem pe sub forma unui patrat perfect: =a²+2ab+b²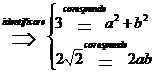se gasesc usor numerele ,b=1.

Pas 3:Ne propunem sa extindem mecanismul de mai sus pentru a descoperi o

formula de simplificare a expresiei : ,

Prin analogie cu pasul doi vom incerca sa gasim doua numere x si y astfel incat =(x+y)² =x+y sau .

Prin identificare se ajunge la :

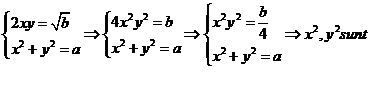
solutiile ecuatiei de gradul al doilea:

t²-at+=0

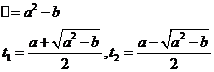
daca a²-b0 !!!

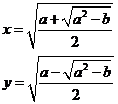de unde rezulta ca:preferam x,y0

Din considerentele anterioare rezulta formula radicalilor compusi:

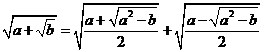daca a²-b0,a,b0

Poate aplicand aceste metode vom reusi sa realizam in cadrul orelor de curs tot ceea ce ne propunem , vom reusi sa demonstram elevilor nostri ca matematica este ,,regina stiintelor"