Minimizarea cheltuielilor de transport. Problema clasica

Minimizarea cheltuielilor de transport. Problema clasica

1. Activitatea de transport. Generalitati

La baza activitatii de transport stau urmatoarele principii:

reducerea la maxim posibil a operatiilor de transport;

mecanizarea operatiilor de transport si asigurarea cerintelor de eficienta economica a acestora;

deplasarea materialelor prin gravitatie, ori de cate ori este posibil;

asigurarea unui flux simplu si rectiliniu al materialelor cu deplasari cat mai scurte, rapide si fara incrucisari sau blocarea circulatiei;

alegerea sistemelor de transport usor adaptabile (elastice).

In sistemele de productie organizate pentru productia de masa sau de serie mare, cu flux de transport stabil, transportul se face, de regula, pe baza de grafic, de itinerariu si marsruturi constante. In celelalte situatii (productie de serie mica sau individuala, caz in care fluxurile de transport sunt variabile) transportul se face pe baza de programe zilnice sau la cerere.

Cresterea coeficientului de folosire a cursei determina reducerea necesarului de material rulant, cresterea productivitatii activitatii de transport si reducerea costurilor in activitatea de transport. Analiza costurilor trebuie sa arate abaterile de la costul normat si, eventual, marimea pierderilor.

Caile de imbunatatire a activitatii de transport intern sunt:

mecanizarea lucrarilor de incarcare-descarcare;

centralizarea lucrarilor de transport;

crearea bazei de reparatii si intretinere a mijloacelor de transport;

sporirea volumului transporturilor care se repeta (aplicarea sistemului pendular si mai ales a sistemului circular);

repartizarea judicioasa a personalului de deservire si organizarea folosirii rationale a mijloacelor de transport.

Pentru programarea activitatii de transport trebuie sa se cunoasca urmatoarele date:

programul de productie al intreprinderii pe perioada considerata;

necesarul de materiale pentru indeplinirea sarcinilor de plan (se extrage din planul de aprovizionare).

Intocmirea unui program de transport intern presupune o pregatire minutioasa prin parcurgerea urmatoarelor etape:

Intocmirea sub forma matriciala a unei situatii cu privire la cantitatile de materiale (pe sortimente) ce urmeaza a se asigura sectiilor de productie (consumatorii C1, C2, C3,, Cn) de la sursele de aprovizionare (depozitele D1, D2, D3,, Dm), asa cum este exemplificat in tabelul 1.

Tabelul 1. Modelul matematic corespunzator unei probleme de transport

1. Se determina distantele dintre obiective in tone-metri, distantele medii de transport, numarul mediu de cicluri de transport, coeficientul mediu de manipulare

2. Se intocmeste balanta capacitatii de transport care evidentiaza plusul sau deficitul de capacitate de transport pentru fiecare obiectiv in parte;

3. Se determina necesarul de mijloace de transport, tinand cont de capacitatea de transport a fiecarui mijloc si de coeficientul de folosire al acestuia.

2 Elaborarea planului optim de transport

Elaborarea planului optim de transport face parte din clasa mult mai larga a problemelor modelate prin retele de transport.

O retea de transport modeleaza o situatie economica in care, dintr-un numar de puncte, numite surse (depozitele) trebuie transportata o anumita cantitate dintr-o substanta, intr-un alt numar de puncte denumite destinatii (consumatori). Situatia extrem de generala expusa, poate fi concretizata intr-un numar deosebit de mare de moduri, specificand daca exista sau nu puncte intermediare intre surse si destinatii, modul in care se face transportul (care sunt rutele posibile, costul transportului pe rute, limite maxime sau minime pentru cantitatea transportata pe fiecare ruta, timpul necesar transportului), scopurile urmarite etc.

3 Minimizarea cheltuielilor de transport (problema clasica de transport)

Se considera aprovizionarea a m consumatori, C1, C2, , Cm din n depozite D1,D2,, Dn cu o singura marfa.

In fiecare depozit Di se gaseste cantitatea de marfa a_i, i 1, 2, , n iar fiecare consumator Cj are nevoie de cantitatea de marfa b_j, j 1, 2, , m.

Costul transportului unei unitati de marfa de la Di la Cj este c_ij.

Scopul modelului este determinarea cantitatilor x_ij de marfa transportata de la depozitul Di la consumatorul Cj astfel incat costul transportului intregii cantitati de marfa sa fie minim. In situatia in care c_ij este infinit (foarte mare), transportul de marfa de la Di la Cj este imposibil.

Problemele in care este indeplinita relatia:

, (3)

se numesc echilibrate.

Modelele matematice ale problemei contin ca restrictii urmatoarele doua conditii:

4. totalul marfii extrase dintr-un depozit sa nu depaseasca existentul in acel depozit, adica:

(4)

5. cantitatea totala primita de un consumator sa nu fie mai mica decat necesarul acelui consumator, adica

(5)

Costul total de transport (functia obiectiv) este dat de relatia:

(6)

Cu cele de mai sus rezulta urmatoarele modele ale problemei clasice de transport:

6. problema echilibrata:

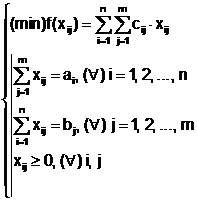(7)

7. problema neechilibrata:

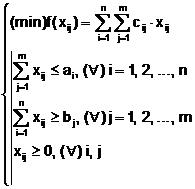(8)

Problema echilibrata este o problema de programare liniara in forma standard si se poate rezolva folosind algoritmul simplex (dupa o re-notare corespunzatoare a necunoscutelor) care se gaseste sub forma de produse program (soft) ca de exemplu AB/QM sau WINQSB.

Pentru rezolvarea problemei neechilibrate trebuiesc aplicate regulile de aducere a ei la forma standard (folosirea variabilelor de compensare).

Exemplul 1. Se considera rezolvarea problemei de transport a unei marfi de la doua depozite D1 si D2 in care se gasesc cantitatile de marfa a₁ respectiv a₂ catre trei consumatori C1, C2, C3 care au necesarul b₁, b₂, b₃.

se considera cazul problemei echilibrate, deci a₁ a₂ b₁ b₂ b₃.

Costurile transportului c_ij de la depozitul i la consumatorul j sunt date de matricea urmatoare:

Problema trebuie sa determine valorile x_ij ale cantitatilor transportate de la depozitul i la consumatorul j care sa asigure costuri minime:

Modelul matematic al problemei este:

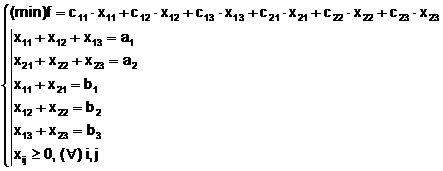(9)

Prin re-notarea necunoscutelor modelul matematic devine:

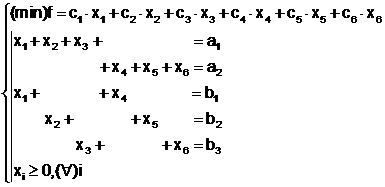(10)

Se constata ca acesta este un model de programare liniara in forma standard care are 6 necunoscute cu matricea A de forma:

(11)

Se poate constata ca o astfel de problema devine foarte repede uriasa. De exemplu o problema de transport cu n = 10 furnizori si m = 10 consumatori va avea m · n = 100 necunoscute, iar matricea A a sistemului: m n = 20 linii si m · n = 100 coloane.

Se observa usor ca rangul matricei r(A) < m + n ceea ce face imposibila aplicarea algoritmului simplex (nu exista o baza de m + n, numarul de linii, vectori coloana liniari independenti necesari in primul pas). Problema se poate rezolva numai prin scrierea problemei extinse.

Daca se considera urmatoarele valori numerice pentru exemplul dat:

Rezolvarea problemei se va face utilizand modulul Linear and Integer Programming din pachetul WINQSB si este prezentata in imaginile urmatoare care reprezinta: fereastra initiala pentru introducerea datelor sub forma tabelara, primul tabel simplex si solutia problemei sub forma tabelara.

3.1. Dualitatea simetrica

Considerandu-se scrierea unei probleme de programare liniara sub forma matriciala, prin definitie modelul primal I se afla in dualitate simetrica cu modelul dual II, conform relatiilor:

I. 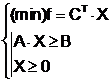(12)

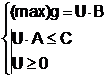II. (13)

Prin conventie se spune ca fiecare model este simetricul celuilalt.

Legatura dintre solutiile celor doua modele este data de urmatoarele doua teoreme:

Teorema 1. Fie o solutie posibila a modelului I si o solutie posibila a modelului II, atunci

Consecinta: Daca solutiile , au proprietatea atunci este optima pentru modelul I, iar - optima pentru modelul II.

Teorema 2 (teorema ecarturilor complementare). Fie , solutii ale modelelor I respectiv II. Ele sunt optime daca si numai daca:

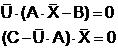(14)

Dualitatea simetrica se aplica atunci cand rezolvarea modelului dual este mai simpla.

3.2. Dualitatea nesimetrica

Un model de programare liniara care nu are nici una din formele I sau II nu se afla in dualitate cu nici un alt model.

Similar dualitatii simetrice, s-au conceptul regulile prezentate mai jos pentru scrierea modelului dual pentru orice model de programare liniara. La scrierea modelului dual se considera urmatoarea clasificare a restrictiilor:

8. pentru criteriul de tip MIN:

restrictia este concordanta

restrictia este neconcordanta

9. pentru criteriul de tip MAX:

restrictia este concordanta

restrictia este neconcordanta

In ceea ce priveste legatura dintre solutiile (optime sau nu) ale celor doua modele, sunt valabile rezultate asemanatoare celor din cazul dualitatii simetrice.

3.3. Rezolvarea problemelor de transport echilibrate prin utilizarea dualitatii

Pentru modelul problemei de transport modelul dual se scrie astfel:

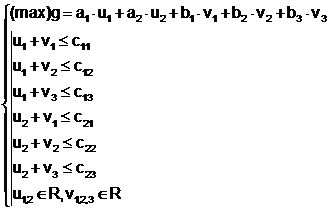(15)

Se constata ca scrierea modelului dual implica adoptarea variabilelor u₁, u₂ corespunzatoare numarului de depozite, respectiv v₁, v₂, v₃ - corespunzatoare numarului de consumatori.

Rezolvarea modelului dual si obtinerea solutiei optime a modelului primal a condus la stabilirea urmatorului algoritm pentru rezolvarea problemelor de transport:

Pas 1. Se alege o solutie de baza avand numarul de componente nenule egal cu .

Pas 2. Se rezolva sistemul determinand o solutie particulara .

Pas 3. Daca pentru o componenta x_αβ 0 avem se cauta o alta solutie, pentru care x_αβ' sa devina nenul

Pas 4. Solutia optima s-a atins atunci cand:

(16)

Exemplul 2. Pentru exemplul rezolvat clasic prin aplicarea algoritmului simplex utilizand pachetul de programe WINQSB, aplicarea algoritmului de mai sus este urmatoarea:

Pas 1: se alege urmatoarea solutie de baza cu m + n - 1 = 4 componente nenule:

Pas 2: se obtine urmatorul sistem de 4 ecuatii cu 5 necunoscute:

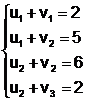
a carui rezolvare conduce la urmatoarea solutie:

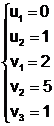
Pas 3: - pentru: x₁₃ = 0, u₁ + v₃ = 1 < c₁₃ = 7;

- pentru: x₂₁ = 0, u₂ + v₁ = 3 < c₂₁ = 4.

Pas 4: se verifica usor ca este indeplinita conditia , rezultand, deci ca solutia de baza adoptata este cea optima

Problema principala in cazul aplicarii algoritmului de mai sus este gasirea unei solutii initiale de baza. Exista o multitudine de metode care incearca nu numai gasirea unei solutii initiale de baza, ci chiar gasirea uneia cat mai buna. Se expun in continuare urmatoarele metode:

Metoda nord-vest;

Metoda minimului pe linii;

Metoda minimului pe coloane;

Metoda costului minim;

Metoda diferentelor maxime.

Schema comuna a acestor metode este urmatoarea:

Pas 1: Se alege o ruta initiala dupa o anumita regula.

Aceasta regula difera in functie de metoda folosita, astfel:

Pas 2: Se transporta pe aceasta ruta maximul posibil. Acest maxim este egal cu minimul dintre cantitatea care mai e disponibila la furnizorul corespunzator acestei rute si cantitatea care mai e necesara la consumatorul corespunzator rutei, in momentul alegerii acestei rute.

Pas 3: Dupa folosirea unei rute este clar ca fie se epuizeaza disponibilul furnizorului corespunzator, fie se asigura intregul necesar al consumatorului corespunzator, fie ambele. Daca se epuizeaza disponibilul furnizorului este clar ca nici o ruta care pleaca de la acesta nu va mai fi folosita si analog, daca se asigura intregul necesar al consumatorului, nici o ruta spre acesta nu va mai fi folosita. Rutele care nu vor mai fi folosite se numesc rute blocate, sunt cele nefolosite inca de pe linia sau/si coloana ultimei rute folosite si se evidentiaza in tabel prin hasurare.

Pas 4: Se alege ruta urmatoare, folosind una dintre urmatoarele metode:

Pas 5: Se reia algoritmul de la pas 2 pana cand nu mai ramane nici o ruta nefolosita sau neblocata.

Rezolvare:

Cei doi algoritmi prezentati mai sus sunt folositi pentru rezolvarea problemelor de transport si de modulul Network Modeling/Transportation Problem din pachetul de programe WINQSB asa cum se exemplifica in imaginile din figura 4.

3.4 Rezolvarea problemelor de transport neechilibrate

Problemele de transport neechilibrate se rezolva prin echilibrarea lor considerandu-se, dupa caz, un depozit sau consumator fictiv care sa echilibreze problema. Evident ca se va considera valoarea zero pentru costul transportului de la depozitul fictiv catre orice consumator respectiv de la orice depozit catre consumatorul fictiv.