Elemente de teoria asteptarii

Elemente de teoria asteptarii

teoria firelor de asteptare ; teoria cozilor

Elementele problemei fenomenului de asteptare :

Sursa multimea unitatilor care solicita un serviciu la un moment dat.

Sosirea unitatilor in sistemul de asteptare determina o variabila

aleatoare X care reprezinta numarul de unitati care intra in

sistem in unitatea de timp.

Sistemul de asteptare, format din:

- Firul de asteptare : este determinat de numarul unitatilor care asteapta (finit sau infinit)

- Statia de serviciu : un lucrator , o masina , etc. care efectueaza serviciul solicitat. Timpul de servire al unei unitati in statia de serviciu este o variabila aleatoare Y

Indicatorii principali ai problemei de asteptare .

m - numarul de unitati ale populatiei din sursa care sosesc in

sistem care poate avea valorile: - ∞ - sistem deschis

- finit - sistem inchis

2) s - numarul de statii de serviciu ;

3) p_n(t) -probabilitatea ca in sistemul de asteptare sa se gaseasca "n"

unitati la momentul "t" oarecare (p_n) ;

4) n(t) - numarul de unitati ce se gasesc in sistemul de asteptare

(fir + serviciu) la momentul "t"; este o variabila

aleatoare cu distributia:

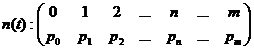
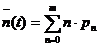- numarul mediu de unitati din sistem la un moment t

n_f(t) - numarul de unitati din firul de asteptare la un moment dat "t";

n_f(t )este o variabila aleatoare,care,tinand cont ca exista unitati

in firul de asteptare atunci cand n > s, are distributia:

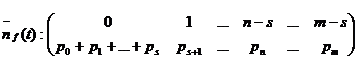
_f(t) s - numarul mediu de unitati care se afla in fir;

n_s(t) -numarul de unitati care sunt servite la un moment "t":

n_s(t) n(t) n_f(t) → variabila aleatoare;

6') (t) (t) - (t) numarul mediu de unitati care sunt servite la momentul t

P (n (t)> k) probabilitatea ca numarul unitatilor din sistem la

momentul "t" sa fie mai mare decat k :

P (n(t)> k) P(n(t)k) (p_o p₁ p_k )

8) timpul mediu de asteptare al unei unitati in fir ;

9) timpul mediu de asteptare al unei unitati in sistem .

1 Legile probabilistice ale sosirilor si servirilor

Fie X variabila aleatoare discreta ce reprezinta numarul de unitati sosite in unitatea de timp, intr-un sistem de asteptare.

In conditiile :

a)     posibilitatea sosirii unei unitati la un moment dat este costanta si nu depinde de ceea ce s-a intamplat anterior ;

b)     posibilitatea unei sosiri intr-un interval de timp (t , t Δt) este propor-

tionala cu lungimea , Δt , a intervalului;

c)     probabilitatea ca in intervalul de timp (t , Δt) , Δt foarte mic, sa avem mai mult de o sosire este aproximativ egala cu zero variabila aleatoare X , are repartitia Poisson , cu parametrul λt

unde :

P_n(t) probabilitatea ca la momentul t, numarul de unitati sosite sa fie

n ;

numarul mediu de unitati sosite in unitatea de timp.

Observatie: Acceptand aceleasi conditii a) , b) , c) si pentru numarul unitatilor servite de catre o statie care lucreaza fara intrerupere , se obtine ca numarul de servicii ce pot fi facute de o statie intr-un timp t , este o variabila aleatoare poissoniana , cu parametru μt , unde μ este numarul mediu de unitati servite in unitatea de timp.

Variabila aleatoare Y₁ , timpul dintre doua sosiri are o repartitie exponentiala

f(t) e ^{- t}

cu valoarea medie

M(Y₁) - intervalul mediu intre doua sosiri consecutive este inversul numarului mediu de sosiri in unitatea de timp.

Observatie: In mod similar,varibila aleatoare Y,timpul dintre doua servicii consecutive are o repartitie exponentiala de parametru μ si deci intervalul mediu dintre doua servicii cosecutive este .

Exemplu:

Cu ajutorul unor metode statistice s-a stabilit ca sosirile la magazia de scule

a unei sectii de prelucrari mecanice sunt o variabila de tip Poisson cu numarul mediu de sosiri de 120 secunde.

Sa se determine:

a)     intervalul mediu dintre doua sosiri consecutive;

b)     numarul mediu de sosiri pe minut;

c)     probabilitatea ca in 75 secunde sa nu fie nici o solicitare.

Rezolvare:

a)     Unitatea de timp: 1 min.

120 .. 60 min λ 2 sosiri /minut intervalul mediu intre 2 sosiri 0.5 min.

b) timpul mediu de servire s20 sec. numarul mediu de unitati servite in

unitatea de timp μ 3 serviri / min.

c) t 75 sec. s

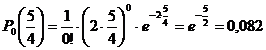
Ecuatiile de stare pentru un fenomen de asteptare in regim stationar

Regim stationar probabilitatile p_n(t) nu depind de momentul "t" , deci sunt constante la orice moment, p_k(t)sp_k. In acest caz se demonstreaza ca:

(1)

λ_0, λ_n-1 - parametrul sosirilor (numarul mediu de sosiri in unitatea de timp) este dependent de numarul unitatilor din sistem ;

μ_{1, ,} μ_n - parametrul serviciilor, numarul mediu de unitati servite in

unitatea de timp, dependent de numarul unitatilor din sistem.

3 Modele de asteptare

Modelul M(∞, 1, 1)

∞ - o infinitate de unitati in sursa (fenomen de asteptare deschis);

1 - un fir de asteptare;

1 - o statie de servire.

λ_n - constant, deoarece populatia din care provin sosirile este suficient de mare;

μ_n - constant, pentru ca exista o singura statie de servire, deci nu depinde de numarul unitatilor din sistem.

Rezulta din (1):

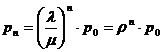
Unde ρ λ/μ este factor de serviciu sau intensitatea traficului

Pentru ρ > 1 - NU este suficienta o singura statie de deservire (avem o aglomerare , crestere a sirului de asteptare).

Pentru ρ < 1 se obtine:

p_o

p_n ρⁿ(1-ρ) ;

numarul mediu de unitati din sistem;

numarul mediu de unitati din fir;

numarul mediu de unitati in curs de servire;

numarul mediu de unitati servite in unitatea de timp;

timpul mediu de asteptare al unei unitati de sistem;

timpul mediu de asteptare al unei unitati de sistem;

P(n>k) ρ^k - posibilitatea ca numarul unitatilor n aflate in sistem 

sa fie mai mare decat un numar k.

Exemplu:

Cu ajutorul unor metode statistice s-a stabilit ca sosirile la magazia centrala de scule deservita de un singur gestionar sunt poissoniene cu media λ 30 persoane pe ora , iar timpul de servire a unei persoane are o repartitie exponentiala cu media de 90 sec. Sa se determine:

a)     Probabilitatea ca in sistemul de asteptare sa nu existe nici un solicitant la un moment dat;

b)     Probabilitatea ca in sistem sa existe 3 solicitanti la un moment dat;

c)     Numarul mediu de solicitanti din sistemul de asteptare, numarul mediu de solicitanti care asteapta (din fir), numarul mediu de solicitanti care sunt serviti la un moment dat si numarul mediu de solicitanti serviti efectiv intr-o unitate de timp.

d)     Timpul mediu de asteptare a unui solicitant pana sa fie servit si timpul mediu de asteptare in intreg sistemul de asteptare.

Rezolvare:

Unitatea de timp: 1 ora;

λ 30 sosiri/ora;

μ 40 serviri/ora;

ρ intensitatea timpului

a) p₀

b)     p₃ ρ³ p₀ 0,75³ 0,25

c)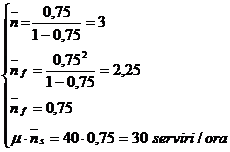    

d)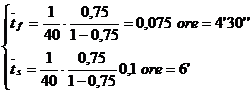

Observatie: Daca firul de asteptare este limitat, adica sistemul de asteptare are capacitatea marginita la N unitati deci in firul de asteptare se pot afla cel mult N - 1 unitati, atunci formulele modelului M(∞, 1, 1) devin:

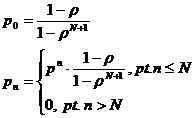
nu mai este necesara conditia ρ<1; unitatile care sosesc in sistem cand n>N, pleaca in alta parte.

Modelul M(∞, 1, s)

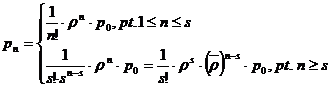
Unde reprezinta factorul de serviciu al tuturor statiilor.

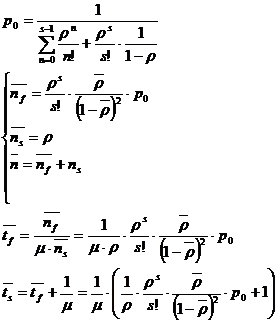
Exemplu: La intrarea in stadion, la un meci de fotbal, au fost amplasate 3 case de bilete. Din datele anterioare se stie ca sosirile sunt poissoniene, cu media λ s 12 spectatori pe minut, iar timpul mesiu de servire - distributie exponentiala negativa - este de 10 sec. Sa se determine numarul mediu de spectatori care asteapta sa intre pe stadion si timpul mediu de asteptare la coada.

12 sosiri/min.

6 serviri/min.

- factorul de serviciu al tuturor statiilor

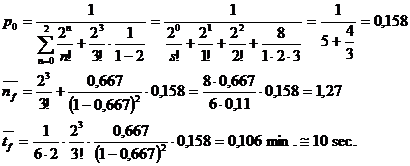
Modelul M(m,1,1)

In cadrul modelelor anterioare s-a presupus ca populatia din sursa este infinita. In practica, de cele mai multe ori, sosirile sunt in numar foarte mare, insa finite. De exemplu: intr-un atelier exista m (numar finit) masini cu aceleasi caracteristici tehnologice si care functioneaza independent unele de altele. Masinile se pot defecta in mod intamplator si sosesc la reparat dupa o lege poissoniana cu parametrul λ; pentru reparatie exista un singur mecanic (statie), iar durata reparatiei unei masini urmeaza o repartitie exponentiala (cu parametrul μ).

Acest exemplu constituie un model de asteptare cu un fir de asteptare, o statie, populatie finita. Pentru determinarea caracteristicilor acestui model se observa ca probabilitatea ca in intervalul de timp Δt sa soseasca in sistem o unitate, atuci cand exista n unitati in sistem din cele m ale sursei, este cu atat mai mica, cu cat numarul unitatilor ramase in sursa este mai mic. De aceea se poate scrie:

Deoarece exista o singura statie, parametrul μ nu depinde de numarul de unitati din sistem, el fiind constant, μ.

Inlocuind in (1) rezulta:

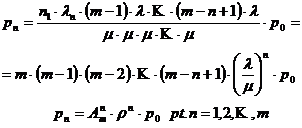(μ de n ori)

Pentru calculul lui p₀ se porneste de la relatia:

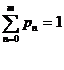
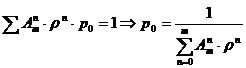
Caracteristicile acestui model vor fi:

- numarul mediu de unitati aflate in sistem:

- numarul mediu de unitati care sunt servite la un moment dat va fi dat de aceeasi expresie ca la modelul modelul M(∞, 1, 1) deoarece exista o singura statie de servire:

- numarul mediu de unitati aflate in fir:

- timpul mediu de asteptare a unei unitati din fir este:

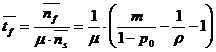
- timpul mediu de asteptare in sistem:

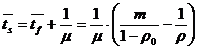
Exemplu: Intr-un atelier cu 10 masini de acelasi tip la defectarea acestora sunt reparate de catre un mecanic. Stiind ca sosirile sunt de tip poissonian cu λs1/5 si durata reparatiei este exponentiala de parametrul μs2, sa se calculeze caracteristicile modelului (se considera unitatea de timp 1 zi s 8 ore).

m

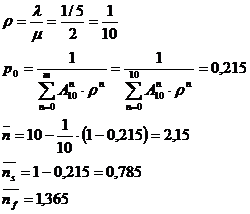
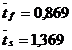
Observatie: Probabilitatea ca trei masini sa fie defecte:

Modelul M(m,1,s)

- Ca si in cazul M(m,1,1), cand populatia sursei este finita parametrul λ, reprezentand numarul mediu al sosirilor pe unitatea de timp, depinde de numarul unitatilor ramase in sursa, fiind proportional cu acestea:

λ_n (m-n) λ

- Celalat parametru, μ - numarul mediu al venirilor pe unitatea de timp, se va scrie ca si in modelul M(∞,1,s).

Cu aceste valori rezulta:

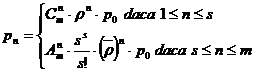
unde: factorul de serviciu al tuturor statiilor

factorul de serviciu al fiecarei statii

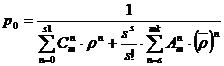
Celelalte caracteristici ale modelului se calculeaza pornind de la relatiile lor de definire prezentate anterior.

Exemplu: Intr-o sectie sunt 9 masini identice si sunt angajati 4 mecanici care intervin numai in momentul in care o masina se defecteaza, pentru a o repara. Stiind ca reparatia unei masini este o variabila aleatoare cu parametrul μ s ½ masini pe ora si ca durata medie de functionare a unei masini fara nici o defectiune este de 5 ore, sa se determine:

a)     probabilitatea ca in sistemul de asteptare sa se gaseasca 3 masini, apoi 4 masini.

b)     Numarul mediu de masini defecte ce asteapta la un moment dat sa fie reparate.

c)     Timpul mediu de asteptare in fir si in sistem.

Rezolvare: Unitatea de timp: ora

m s λ μ

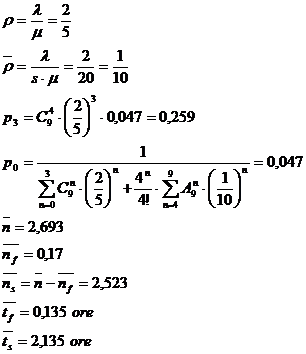
In multe dintre fenomenele de asteptare preocuparea principala este reducerea timpilor de asteptare/inactivitate proiectand spatii de servire cat mai satisfacatoare, dar evident nu se poate merge cu marirea acestora la infinit. Deci va fi necesara determinarea unui plan optim de asteptare care sa fie cat mai convanabil din punct de vedere economic. Pentru aceasta se studiaza diversele variante ale modelului de asteptare, comparandu-se indicatorii intre ei: timpi de asteptare, numar de statii. In acelasi timp trebuiesc calculate cheltuielile globale, pe unitatea de timp ale fiecarei variante din care se alege cea cu cheltuielile globale minime.