Implementarea algebrei booleene - logica pozitiva si logica negativa

IMPLEMENTAREA ALGEBREI BOOLEENE

Un circuit logic este un circuit fizic (concret,palpabil),de regula electric sau mai degraba electronic,care implementeaza (transpune in realitate) una sau mai multe functii booleene (logice).

Circuitele logice sunt construite din componente fizice care au un comportament definit de doua stari distincte.De exemplu un contact poate fi inchis sau deschis,un transistor poate fi blocat sau saturat,un bec poate fi aprins sau stins,un motor poate fi pornit sau oprit,etc.Deoarece efectele enumerate nu au sens in lipsa semnalelor (a marimilor fizice,tensiune sau curent) este necesara realizarea de corespondente intre valorile logice 0 si 1 si nivelele marimilor fizice.

In tabelul acesta se face analogia intre functiile logice si circuitele logice si este reprezentata schema bloc a unui circuit logic cu n intrari si m iesiri.

* Shema bloc a unui circuit logic

1. LOGICA POZITIVA SI LOGICA NEGATIVA

Functie de modul cum facem asocierea dintre valorile logice 0 si 1 si nivelele semnalului putem defini logica pozitiva si logica negativa.

Observatii:

Ne vom referi in continuare mai ales la nivelele de tensiune.

Nivelul scazut de tensiune il notam cu L (Low) iar cel ridicat cu H (High).

In logica pozitiva nivelului formal L ii asociem 0 logic iar nivelul H,1 logic.

In logica negative nivelului formal H ii asociem 0 logic si nivelul L,1 logic.

In figura de mai jos sunt reprezentate cate cinci posibilitati de combinare a nivelelor H si L relative la potentialului 0V.

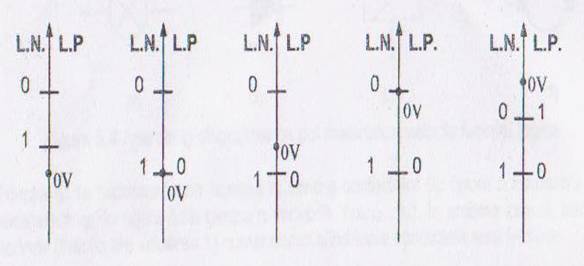
Folosind tabelul de mai sus,tabel de adevar cu niveluri de tensiune ale unui ipotetic,sa se scrie expresia functiei realizate de circuit,in cele doua logici.

*In acest tabel extragem expresia functiei realizata de circuitul ipotetic in logica pozitiva (f=xy ) ,iar in celalalt tabel expresia functiei in logica negativa:

f=xy + x + y =xy + x + xy + y= x +y

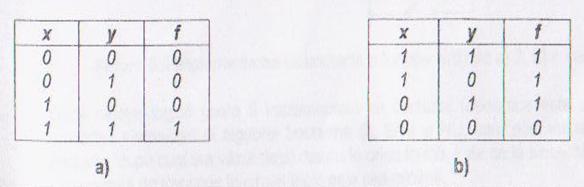
Observatie! Acelasi tabel de adevar in nivele de tensiune se transpune,in cele doua logici,in exprssii diferite.

2.IMPLEMENTAREA FUNCTIILOR LOGICE IN CIRCUITE CU CONTACTE

Circuitele logice pot fi realizate cu contacte ce pot apartine unor aparate electrice de comutare cum ar fi: butoane de comanda,comutatoare,intrerupatoare,limitatoare,contactoare,relee,s.a.

Indiferent carui tip de aparat ii apartine contactul,indiferent de caracteristicile sale tehnice si indiferent de modul de integrare constructive in ansamblul aparatului,contactelor sunt de doua feluri:

Normal deschis,cand prin contact,atunci cand nu este actionat nu circula curent;

Normal inchis,cand prin contact circula curent atunci cand nu este actionat.

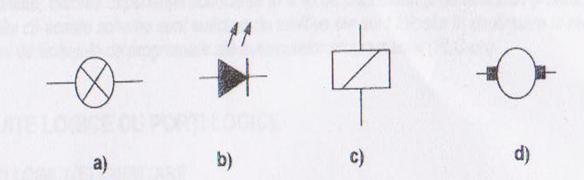
* Contacte : a)normal deschis

b)normal inchis

Observatie! In continuare vom lua in considerare logica pozitiva.

Contactele se asociaza variabilelor booleene astfel:

Contactul normal deschis se asociaza variabilei simple,nenegate (x,y,a,b..).Atunci cand variabila are valoarea 1 logic contactul este inchis (actionat),efectul fiind acela ca prin el poate sa circule curentul (curentul are o valoare diferita de 0) iar cand variabila are valoarea 0 logic contactul este deschis (neactionat) prin el neputand sa treaca current (curentul are valoare 0).

Contactul normal inchis se asociaza variabilei negate (,,,,etc).Atunci cand variabila valoarea 0 logic (variabila negata are valoare 1 logic) contactul este inchis (neactionat),efectul fiind acela ca prin el poate sa circule curentul (curentul are o valoare diferita de 0) iar cand variabila are valoarea 1 logic (variabila negata are valoarea 0 logica,contactul este deschis (actionat) prin el neputand sa treaca current (curentul are valoarea 0).

Pentru a pune in evidenta valoarea functiei realizate de circuitul logic se utilizeaza de regula becuri dar in practica se pot utiliza si diverse alte aparate sau dispozitive cum ar fi:

• Diode    electroluminiscente (LED-uri)
• Relee,contactoare (infasurarile lor de comanda)
• Servomotoare

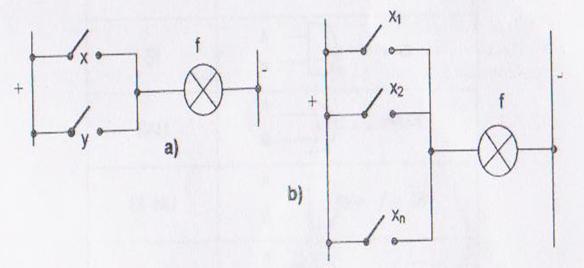
Putem implementa acum functii logice de baza SI si SAU cu contacte:

Functia SI se realizeaza prin legarea in serie a contactelor.In ambele cazuri,becul se aprinde (functia are valoarea 1 ) numai atunci cand toate contactele sunt inchise.

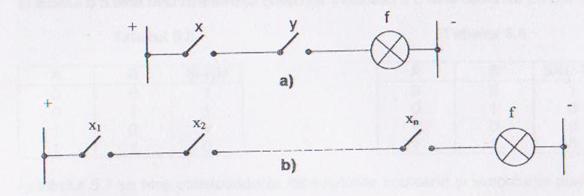
Functia SAU se realizeaza prin legarea in paralel a contactelor.In exemplul dat,becul se stinge (functia are valoarea 0 ) numai atunci cand toate contactele sunt deschise.

Orice functie logica poate fi implementata cu contacte (deoarece este construita cu operatorii elementari ai algebrei booleene SI,SAU si NU,care sunt implementabili cu contacte,dupa cum s-a vazut deja) dar nu in orice forma.Este de la sine inteles ca forma convenabila de transpus in circuit logic este cea minima.

Exemplu: Sa se implementeze cu contacte functia booleana     f(x,y,z)=y+yz+xyz.

Rezolvare: Se incearca mai intai minimizarea functiei cu ajutorul diagramei Veitch (sau prin calcul boolean).

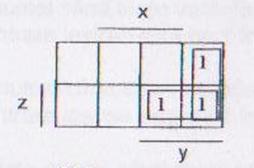
Expresia minima a functiei va fi: f = y + yz = y(+z)

Ambele forme ale functiei minimizate pot fi implementate in circuit logic.

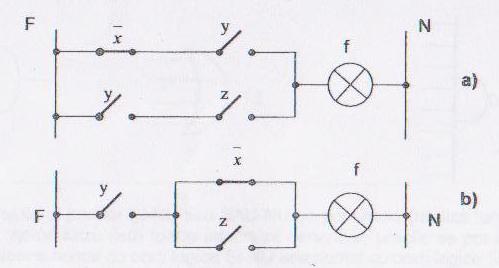
Observatii:

Varianta din figura de mai sus b) este mai convenabila deoarece utilizeaza un nr mai mic de contacte.Operatia prin care s-a ajuns la aceasta forma se numeste factorizare si duce la optimizarea formei functiei.

Alimentarea circuitului s-a facut in current alternativ,F-faza,N-nul.

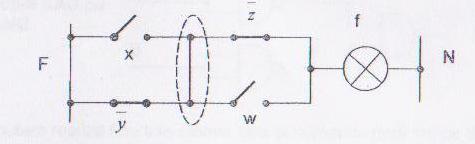
Rezolvare: Cele doua noduri din figura pot fi unite intr-unul singur f = (x +)(+ w)

Observatie: Chiar daca implementarile cu contacte ale functiilor logice nu mai sunt de actualitate,datorita experientei accumulate in timp de proiectanti si de utilizatori si datorita faptului ca aceste scheme sunt suficient de intuitive ele sunt folosite in continuare la nivel formal de limbajele de programare ale automatelor programabile (PLC-uri).

3.CIRCUITE LOGICE CU PORTI LOGICE    3.1 PORTI LOGICE ELEMENTARE

Functiilor booleene elementare SI (AND), SAU (OR),NU (NOT) carora li se adauga si circuitele SI-NU (NAND) si SAU (NOR),le corespund circuite (electronice) logice elementare numite porti logice elementare.

In tabelele de mai jos este descrisa functia SI - NU iar in tabelul celalalt este descrisa functia SAU - NU.

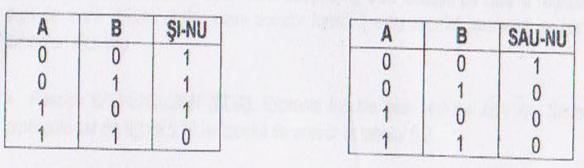
In tabelul de mai jos se face corespondenta intre functiile booleene si simbolurile portilor ce le implementeaza.

Atat tabelul de adevar cat si simbolurile portilor corespund functiilor cu numai doua variabile,dare le pot fi usor extinse pentru un numar n de intrari.Functionarea portilor cu un numar n de intrari poate fi descrisa astfel:

Poarta SI realizeaza 1 logic la iesire numai cand toate intrarile sunt pe 1 logic;pentru oricare alta combinatie a variabilelor de intrare iesirea este pe 0 logic.

Poarta SAU realizeaza 0 logic la iesirea numai cand toate intrarile sunt pe 0 logic;pentru oricare alta combinatie a variabilelor de intrare iesirea este pe 1 logic.

Poarta SI-NU realizeaza 0 logic la iesire numai cand toate intrarile sunt pe 1 logic,pentru oricare alta combinatie a variabilelor de intrare iesirea este pe 1 logic.

Poarta SAU-NU realizeaza 1 logic la iesire numai cand toate intrarile sunt pe 0 logic pentru oricare alta combinatie a variabilelor de intrare iesirea este pe 0 logic.

Exemplu: Porti logice cu numar de intrari mai mare de 2

SI cu 3 intrari SAU cu 4 intrari SI-NU cu 8 intrari

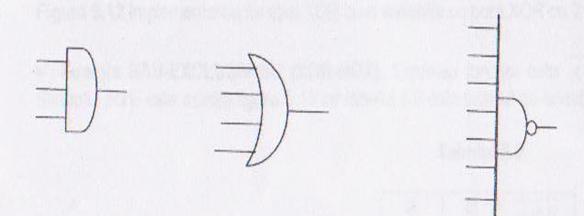
Cu ajutorul portilor SI-NU sau SAU-NU se pot emula (realize functional) portile SI,SAU,NU.Acest lucru este foarte important deoarece,practice se pot implementa orice functie booleene numai cu porti logice SI- NU sau numai cu porti logice SAU-NU.

Realizarea functiei NU cu porti logice SI-NU

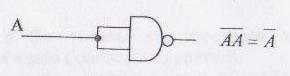
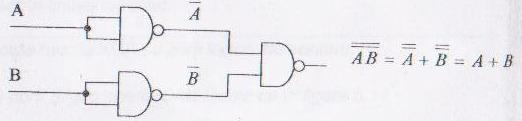
Realizarea functiei SI cu porti logice SI-NU

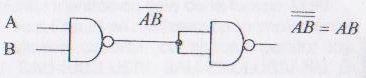
Realizarea functiei SAU cu porti logice SI-NU

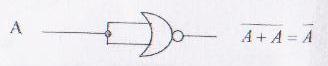
Realizarea functiei NU cu porti logice SAU-NU

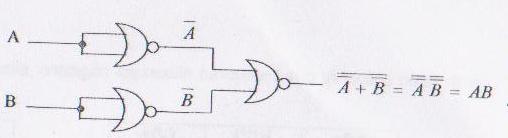
Realizarea functiei SI cu porti logice SAU-NU

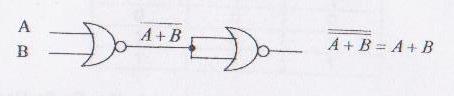
Realizarea functiei SAU cu porti logice SAU-NU

PORTI LOGICE COMPLEXE

Sunt porti logice ce corespund unor circuite logice realizate cu ajutorul portilor logice elementare.Structura lor nu este foarte complicate,insa functiile pe care le realizeaza sunt de mare utilitate si de aceea acestor functii li s-au asociat operatori iar portilor simboluri distincte.

-Functia SAU-EXCLUSIV (XOR).Expresia functiei este A B = + B

   

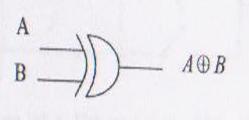
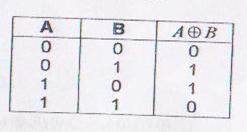
Functia XOR se mai numeste si Semisumator sau Detector de paritate.Semisumator pentru ca efectueaza adunarea a doi biti fara sa tina cont de transportul de la rangul inferior si detector de paritate pentru ca functia ia valoarea 1 numai daca numarul de variabile care iau valoarea 1 este impar.

Se poate demonstra ca functia XOR este asociativa si avem:

f= ABC AB)C=A(BC)

Implementarea cu porti XOR cu doua intrari a functiei este ilustrata mai jos:

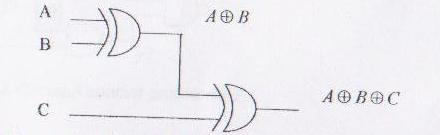
Realizarea functiei XOR cu 3 intrari cu ajutorul portilor XOR cu 2 intrari.

Pentru o functie XOR cu n variabile,circuitul rezultat prin implementare cu porti XOR cu doua intrari este ilustrat in figura de mai jos.

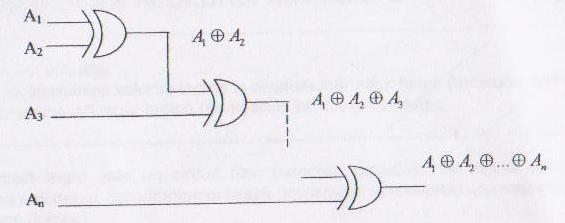
Functia SAU-EXCLUSIV-NU (XOR-NOT).Expresia functiei este =AB+.

   

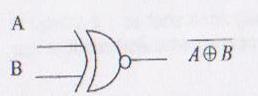
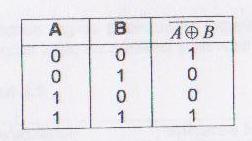
Functia SAU-EXCLUSIV-NU se mai numeste si Coincidenta sau Identitate,adica functia are valoarea 1 numai daca variabilele sunt egale (identice sau coincid).Pentru implementarea functiei XOR-NOT cu mai multe variabile cu porti XOR-NOT cu doua intrari,se utilizeaza scheme cu configuratii identice cu cele de la functia XOR.Circuitele logice complexe (combinationale) se realizeaza prin implementarea functiei booleene pe care trebuie s-o realizeze circuitul,cu ajutorul portilor logice elementare NU,SI,SAU,SI-NU,SAU-NU,SAU-EXCLUSIV,SAU-EXCLUSIV-NU.Este un fel de scriere a functiilor in limbaj simbolic.

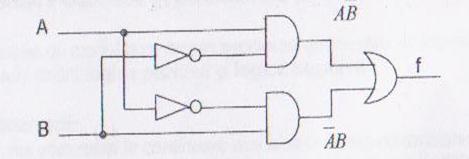
Exemplu: Sa se implementeze functia XOR cu porti logice elementare.

Rezolvare: f = AB=+AB

Vom utiliza doua porti NU,doua porti SI si o poarta SAU legate ca in figura de mai jos.