Problemele rezistentei materialelor

PROBLEMELE REZISTENTEI MATERIALELOR

1.1. Obiectul si problemele rezistentei materialelor

In mecanica teoretica corpul solid este considerat rigid, nedeformabil, adica oricat de mari ar fi fortele aplicate asupra lui acesta nu se deformeaza.

In realitate, corpurile solide care intervin in tehnica si in viata de toate zilele nu pot suporta forte exterioare, oricat de mari. In prezenta fortelor, acestea se deformeaza, iar cand deformatiile depasesc anumite limite, poate surveni ruperea. Rezistenta materialelor este stiinta care introduce in calcule proprietatea corpurilor de a se deforma in scopul de a determina daca ele rezista sau nu sarcinilor aplicate.

Obiectul rezistentei materialelor cuprinde urmatoarele aspecte:

- dimensionarea organelor de masini sau elementelor de constructii astfel ca sa reziste in bune conditii sarcinilor date,

- verificarea daca piesele construite rezista sau nu sarcinilor aplicate.

In calculele de rezistenta materialelor trebuie sa se aiba in vedere in primul rand fortele dinafara (sarcinile) care actioneaza asupra corpurilor, dar in acelasi timp trebuie sa se aiba in vedere si natura materialului din care acestea sunt facute. Adica trebuie sa se tina seama si de caracteristicile mecanice ale materialelor. Acestea se determina pe cale experimentala in laborator. Sub acest aspect rezistenta materialelor are un puternic caracter experimental. In afara de acesta, rezistenta materialelor are si un caracter economic, caci inginerul de conceptie trebuie totdeauna in proiectare sa aleaga solutia cea mai economica. Piesa proiectata trebuie sa reprezinte un minimum din punct de vedere al costului de obtinere a ei.

1.2. Clasificarea corpurilor in rezistenta materialelor

Constructiile sunt alcatuite din elemente constitutive denumite elemente de constructii, iar masinile din parti denumite organe de masini. Formele elementelor de constructii si organelor de masini sunt foarte variate dupa rolul functional respectiv. Calculul de rezistenta se aplica acestora pe forme schematice. Din acest punct de vedere se poate face urmatoarea clasificare a corpurilor in rezistenta materialelor:

- bare sau corpuri care au una din dimensiuni mult mai mare decat celelalte doua. Caracteristice pentru o bara sunt forma si dimensiunile sectiunii transversale si forma si dimensiunile axei barei (linia care uneste centrele de greutate al sectiunii transversale). Din acest punct de vedere putem avea bare drepte, curbe sau cotite ori bare de sectiune circulara, patrata etc. Barele care nu pot prelua decat eforturi de intindere din cauza grosimii lor foarte mici se numesc fire.

Barele solicitate la intindere se numesc tiranti, la compresiune arbori, la incovoiere grinzi, iar la rasucire arbori.

- placi sau corpuri care au una dintre dimensiuni mult mai mica ca ordin de marime decat celelalte doua. Caracteristice pentru o placa sunt forma si dimensiunile suprafetei mediane (locul geometric al punctelor de la jumatatea grosimii) si grosimea sa. Dupa cum suprafata mediana este plana sau curba, placile sunt plane sau curbe (invelitori). Dupa forme, placile pot fi circulare, dreptunghiulare, patrate, etc., iar dupa grosime, placi groase, placi de grosime obisnuita, placi subtiri. Placile care datorita grosimii foarte mici nu pot rezista decat la intindere se cheama membrane.

- blocuri sau corpuri masive pentru care toate trei dimensiunile masurate dupa directiile unui sistem de trei axe rectangulare au acelasi ordin de marime. Din aceasta categorie fac parte fundatiile cladirilor si ale masinilor, bilele, rolele, etc.

Rezistenta materialelor se ocupa mai ales de studiul barelor sub toate aspectele si da in parte si unele solutii pentru placi. Prin metodele sale elementare (cum se numesc in teoria elasticitatii si plasticitatii), rezistenta materialelor nu poate solutiona decat putine din problemele placilor si nici una din cele ale masivelor. Calculul exact al placilor ca si calculul masivelor este posibil numai cu ajutorul teoriei elasticitatii si plasticitatii.

1.3. Forte interioare si exterioare. Metoda sectiunilor. Solicitari simple si compuse.

Orice element de constructie sau organ de masina, in ansamblul in care lucreaza este supus actiunii unor forte externe care se aplica pe suprafata pieselor si sunt in acest caz forte de suprafata, fie masei pieselor fiind in acest caz forte masice (de greutate, de inertie etc). Fortele de suprafata si masice poarta denumirea de forte exterioare sau sarcini, ele reprezentand actiuni externe asupra elementelor de constructii si organelor de masini. In afara de aceasta, asupra pieselor (elemente de constructii si organe de masini) se mai aplica inca o categorie de forte externe: reactiunile sau fortele de legatura, masurand actiunea pieselor vecine cu care o anumita piesa vine in legatura in ansamblul in care functioneaza. Dupa cum s-a aratat mai inainte, fortele externe (de suprafata, masice si de legatura) actionand asupra corpurilor solide produc deformarea acestora adica modificarea distantei dintre particulele materiale care compun corpul. Deformarea insa nu este oricat de mare, decat in cazuri extreme cand corpul se rupe, se divide. Ea este in general pe masura fortelor externe aplicate si este limitata de aparitia si existenta in interiorul corpului a unei categorii de forte specifice rezistentei materialelor (mecanicii solidului deformabil in general) si anume fortele interne. Fortele interne se nasc si cresc odata cu deformatiile, adica odata cu aplicarea sarcinilor externe asupra corpurilor. Ele se opun deformarii corpului (sunt orientate in sens invers cresterii deformatiilor) si produc - in cazul deformatiilor elastice - revenirea corpului la forma si dimensiunile initiale atunci cand inceteaza sa actioneze fortele externe. Fortele interne masoara interactiunea particulelor din corp. Cat timp corpul este nesolicitat exterior (forte externe zero), se presupune ca intre particulele corpului nu se exercita interactiuni. Sarcinile externe aplicate corpului tind sa varieze distanta dintre particulele lui. Atunci, la aceasta tendinta de modificare a distantei, se nasc intre particulele vecine forte egale si de sensuri contrare, fie de atractie (cand distanta intre particule tinde sa creasca, fie de respingere, cand distanta tinde sa scada. Acesta este mecanismul nasterii fortelor interioare in corpurile deformabile si ele se pun in evidenta prin metoda sectiunilor. Conform cu aceasta metoda se presupune corpul sectionat cu un plan imaginar in doua bucati (fig. 1.1).

Echilibrul fiecarei bucati astfel separata (a fiecarui tronson) va fi asigurat numai daca in fiecare punct din sectiunea sa (obtinuta prin planul imaginar de taiere) vom introduce cate o forta marcand actiunea particulelor din tronsonul inlaturat. Aceste forte actioneaza in realitate asupra tronsonului respectiv si in situatia corpului incarcat cu fortele externe si nesectionat. Totalitatea acestor forte reduse in centrul de greutate al sectiunii formeaza un torsor, zis torsorul fortelor interne din sectiune. Componentele si ale torsorului se mai numesc si eforturi.

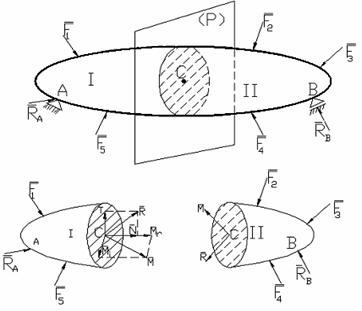
Fig. 1.1

In fig. 1.1 s-a prezentat corpul actionat de un sistem de forte F₁F₂, . .F₅. Fortele de legatura sunt reprezentate prin R_A si R_B (care se determina prin ecuatiile echilibrului static).

Corpul se presupune sectionat prin planul (P) in tronsoanele I si II. In centrul de greutate C al sectiunii fiecarui tronson sunt introdusi torsorii de reducere in C a fortelor interne din fiecare punct al sectiunii respective. Pe figura, aceste forte repartizate pe sectiune (fortele din fiecare punct) nu s-au mai reprezentat. Se face remarca ca cei doi torsori introdusi in sectiunile celor doua bucati de corp au componentele R si M egale ca modul si de sensuri contrare pe baza principiului actiunii si reactiunii. Se poate dovedi dealtfel simplu acest lucru, pe baza echilibrului fiecarui tronson si al corpului nesectionat. Pentru aceasta sa notam componentele partii stangi cu R_I si M_I si ale partii drepte cu R_II si M_II. Scriind pentru tronsoanele I, II si pentru corpul nesectionat ecuatiile de echilibru, rezulta:

(1.1)

(1.2)

(1.3)

(1.4)

(1.5)

(1.6)

Din relatiile (1.1) , (1.3) si (1.5) se obtine imediat

(1.7)

iar din relatiile (1.2), (1.4) si (1.6),

(1.8)

Descompunand vectorii si in componentele lor dupa normala la planul sectiunii si dupa o directie in planul sectiunii, se obtin componentele notate pe figura cu , , , . Componenta N a rezultantei dupa directia normala se numeste forta normala sau forta axiala in cazul barelor (cand sectiunea se ia de obicei perpendiculara pe axa barei, iar normala la sectiune are directia axei barei). Componenta T din planul sectiunii se numeste forta taietoare. Componenta M_r dupa axa barei, a momentului M, se numeste moment de rasucire sau de torsiune. Componenta M_i din planul sectiunii, a momentului M, se numeste moment incovoietor. Cele patru componente N, T, M_i, M_r ale fortelor interioare in sectiunea transversala se numesc eforturi. Cand corpul este astfel actionat incat in sectiunea practicata apare numai una din componentele N, T, M_i, M_r, se spune ca el este supus unei solicitari simple.

Solicitarile simple sunt deci de patru feluri:

- solicitarea de intindere - compresiune data de prezenta in sectiune a efortului normal N (intindere cand efortul este orientat dinspre sectiune in afara si compresiune in sens contrar).

- solicitarea de lunecare, forfecare sau taiere data de prezenta in sectiune numai a fortei taietoare T.

- solicitarea de incovoiere data de prezenta in sectiune numai a momentului incovoietor M_i cu vectorul orientat in planul sectiunii.

- solicitarea de rasucire sau torsiune data de prezenta in sectiune a momentului M_r, cu vectorul orientat dupa axa barei.

Daca sistemul de sarcini externe lucreaza asupra corpului de asa natura incat in sectiunea considerata avem cel putin doua din componentele N, T, Mi, Mr, se zice ca avem o solicitare compusa.

Se intelege ca exprimarea interactiunii prin eforturile N, T, M_i, M_r concentrate in centrul de greutate al sectiunii este o reprezentare schematica a fenomenului, de care rezistenta materialelor se serveste intr-o prima etapa de calcul a sa. Problema de baza a rezistentei materialelor este aceea de a determina legea de distributie a eforturilor pe sectiune si a gasi valorile acestor eforturi in fiecare punct al sectiunii cand se cunosc eforturile concentrate N, T, M_i, M_r determinate pe baza legilor mecanicii teoretice.

Vom preciza de pe acum faptul ca in cazul barelor, sectionarea pentru calculul eforturilor se face cu plane perpendiculare pe axa acestora.

1.4. Tensiuni

Se considera un element de suprafata dA din sectiunea transversala a unui corp solicitat de sarcini externe (fig. 1.2). Elementul dA fiind infinitezimal se poate considera ca fortele interioare din sectiunea corespunzatoare lui, sunt uniform repartizate. Rezultanta acestora sa o notam cu dF si ea va fi aplicata in centrul suprafetei dA.

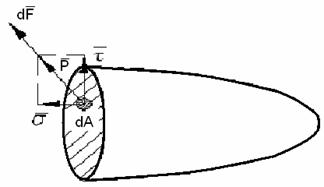
Fig. 1.2

Efortul corespunzator unitatii de suprafata se cheama tensiune si se obtine sub forma,

(1.9)

Tensiunea p, de aceiasi directie cu dF poate fi inlocuita prin componenta sa dupa normala la sectiune si o componenta in planul sectiunii. Componenta normala s, formeaza ceea ce se cheama in toate ramurile mecanicii solidului deformabil tensiune normala iar componenta tangentiala , tensiune tangentiala. Tensiunea s reprezinta un efect de intindere-compresiune (dupa sens) exercitat de partea de corp inlaturata asupra celei ramase. Tensiunea tangentiala reprezinta un efect de lunecare, forfecare sau taiere.

Intre tensiunea p si componentele sale exista relatia:

P² = s (1.10)

Relatia dimensionala pentru tensiuni este FL^-2, unitatea de masura cea mai uzuala fiind MP_a = 10⁶ N/m² .

Se precizeaza de pe acum faptul ca pentru a cunoaste starea de tensiuni intr-un corp solicitat, este suficient sa se cunoasca in fiecare punct si pentru toate planele ce se pot duce prin el, tensiunea normala si tangentiala. Notiunile de tensiune normala si tangentiala sunt fundamentale pentru rezistenta materialelor, ca de altfel pentru toate ramurile mecanicii solidului deformabil. Cu ajutorul lor in teoria elasticitatii este descrisa starea de tensiuni in jurul unui punct (prin care trebuie sa se inteleaga tensiunile normale si tangentiale pe infinitatea de plane care se pot duce prin punctele respective din corp).

Cunoasterea tensiunilor normale si tangentiale in corpurile deformabile, solicitate de sarcini exterioare, este problema fundamentala pentru toate ramurile mecanicii solidului deformabil. Rezistenta materialelor, ca ramura a acestei mecanici si studiind in primul rand barele, urmareste prin metodele sale elementare sa determine distributia de tensiuni normale si tangentiale in sectiunile transversale ale barelor, in primul rand.

1.5. Deformatii si deplasari

S-a aratat deja ca rezistenta materialelor se deosebeste de mecanica teoretica prin faptul esential ca introduce in calcule deformabilitatea corpurilor sub actiunea solicitarilor externe.

Deformatiile corpurilor depind de o serie intreaga de factori: de forma si marimea corpului solicitat, de fortele care-l incarca, precum si de natura materialului corpului respectiv. Insa oricat de complicate ar fi aceste deformatii, se poate face o analiza a lor rationand in felul urmator. Se considera in mod imaginar corpul compus dintr-o multime de elemente in forma de cuburi elementare constituind unele langa altele, corpul asa cum se constituie un zid din caramizile sale. (fig.1.3).

In urma deformarii corpului, edificiul imaginat din cuburi se va deforma si el, astfel ca in general lungimile muchiilor cuburilor se vor modifica si de asemenea se vor modifica si unghiurile lor drepte. Acesta este modul cel mai general de a privi deformarea unui cub. Cunoscand variatia lungimilor muchiilor ca si modificarea unghiurilor pentru toate cuburile ce compun corpul, vom cunoaste starea de deformatii pentru corpul solicitat.

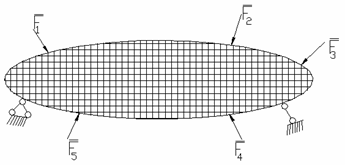
Fig. 1.3

Prin urmare, deformatiile se definesc in general prin variatii de lungime a unor linii drepte si prin variatii de unghiuri drepte. Se vorbeste legat de aceasta de doua categorii de deformatii: deformatii liniare si deformatii unghiulare. Daca un segment liniar are lungimea in stare nesolicitata a corpului l_o, iar aceasta lungime devine dupa solicitare l₁, diferenta Dl = l₁ - l₀ se numeste lungire absoluta daca este pozitiva si scurtare absoluta daca este negativa. Raportul urmator se va numi in mod corespunzator lungire specifica sau scurtare specifica:

(1.11)

Lungirile si scurtarile se masoara in cm sau mm. Lungirile si scurtarile specifice sunt marimi adimensionale.

Exemplul practic din fig. 1.4 pune in evidenta lungirile si lungirile specifice. Bara este solicitata la intindere omogena prin forta F aplicata pe axa ei in capat. Se constata ca bara se lungeste luand forma punctata.

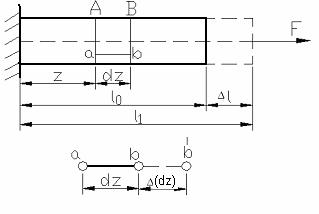
Fig. 1.4

Lungirea prin deformare este l₁-l₀. In cazul unei stari de eforturi neomogena deformatiile variaza in corp de la un punct la altul fiind necesara in acest caz trecerea la limita pentru obtinerea lungirii sau scurtarii specifice:

    (1.12)

Se face observatia importanta ca deformatiile specifice liniare, cum se mai numesc lungirile si scurtarile specifice, sunt asociate totdeauna cu tensiunile normale s in sensul ca ele reprezinta efectul acestor tensiuni. Se va vedea mai departe ca aceasta legatura comporta aspecte mai complexe.

Deformatiile unghiulare specifice, sau lunecarile specifice, sunt marimi adimensionale masurand variatii de unghiuri drepte in radiani. Lunecarile specifice trebuiesc puse in legatura cu tensiunile tangentiale. Ele reprezinta efectul acestor tensiuni.

Experienta arata ca daca pe fetele opuse ale unui cub elementar lucreaza tensiuni tangentiale cu sensuri contrare (fig. 1.5), atunci cubul se deformeaza ca in figura inregistrandu-se o anumita variatie a unghiului dintre fete, initial drept. Marimea este denumita lunecare specifica si se masoara evident in radiani.

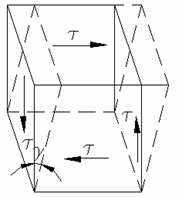
Fig. 1.5

Lunecarea specifica este pozitiva cand masoara micsorarea unghiului drept si negativa cand masoara cresterea acestuia.

Prin deformatiile specifice liniare ε si unghiulare putem caracteriza complet starea de deformatii dintr-un corp solicitat.

Marimile s , caracterizeaza complet starea de tensiuni si de deformatii a corpurilor solicitate. Determinarea acestora pentru barele solicitate este problema de baza a rezistentei materialelor si problema fundamentala a teoriei elasticitatii pentru corpurile elastic deformabile.

Fig. 1.6

Prin deformarea corpurilor, diferitele puncte ale lor isi modifica pozitia fata de cea pe care o au in starea nesolicitata acestora. Drumul parcurs de un punct in procesul deformarii se numeste deplasare. Astfel pentru bara AB din figura 1.6, actionata in A de forta F, bara care prin deformare capata pozitia punctata, deplasarea punctului A este AA'.

Este bine sa se faca cu aceasta ocazie deosebirea intre deplasarile datorita deformatiilor si deplasarilor de corp rigid, adica cele care se produc fara deformarea corpului. Rezistenta studiaza numai prima categorie de deplasari.

1.6. Relatia intre tensiuni si deformatii specifice. Curba caracteristica a materialelor. Legea lui Hooke.

S-a vazut ca notiunile fundamentale ale rezistentei materialelor sunt fortele interioare si deformatiile. Calculele rezistentei materialelor, ca si ale tuturor ramurilor mecanicii solidului deformabil, ar fi complet lipsite de sens daca nu ar tine seama de legatura fizica ce exista intre cele doua categorii de marimi, forte interioare si deformatii. Prima categorie reprezinta marimi de natura mecanica iar a doua de natura geometrica. Legatura intre ele ne este data pe cale experimentala. Incercarile teoretice de a stabili aceasta legatura nu au condus pana acum la rezultate asimilabile pentru mecanica solidului deformabil.

Comportarea materialelor la actiunea fortelor se cerceteaza prin incercari de laborator. Experimentarile se efectueaza pe o proba solicitata omogen, solicitarea depinzand de un singur parametru, masurand variatiile dimensiunii probei odata cu variatia solicitarii. Se traseaza pe baza acestor masuratori o curba experimentala coreland cele doua categorii de marimi mecanice si geometrice.

Incercarea reprezentativa pentru materiale, permitand punerea in evidenta a majoritatii proprietatilor fizico-mecanice ale acestora este incercarea de intindere. Pentru o astfel de incercare se construiesc epruvete tip. Pentru metale aceste epruvete au forma unor bare cilindrice de sectiune rotunda sau dreptunghiulara cu capetele ingrosate permitand prinderea in masina de incercat (STAS 200-76). In zona centrala a epruvetei asupra careia se aplica de catre masina de incercat forte de intindere F la capete, se realizeaza o solicitare cu tensiunea normala:

(1.12) A - fiind aria sectiunii transversale a epruvetei.

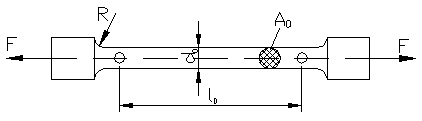
Fig. 1.7

Deformarea epruvetei este urmarita pe o portiune calibrata a sa l₀, prelucrata la dimensiuni precise si marcata prin doua repere pe epruveta.

Raportand lungirea Dl la dimensiunea l₀ dintre repere se obtine lungirea specifica

(1.13)

Curba care leaga tensiunea de lungirea specifica ε se numeste curba caracteristica a materialului. Pentru otelul moale ea are aspectul din fig. 1.8.

Pe diagrama se disting cateva puncte caracteristice. Punctul P marcheaza limita de proportionalitate a materialului: pentru tensiuni mai mici decat _p tensiunile sunt proportionale cu deformatiile specifice. Aceasta proportionalitate intre tensiunile si deformatiile specifice, pentru valorile tensiunii inferioare limitei de proportionalitate, formeaza legea lui Hooke care se scrie matematic:     (1.14)

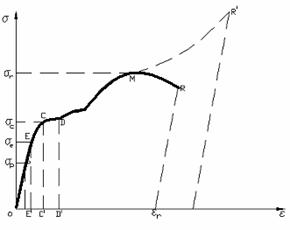
Fig. 1.8

Coeficientul de proportionalitate E, se numeste modul de elasticitate longitudinala sau modulul lui Young. E se masoara evident in unitatile tensiunii . Pentru oteluri are valoarea E = 2,1 ∙ 10⁵ MPa sau 2,1 ∙ 10⁶ daN/cm².

Punctul E marcand limita de elasticitate a materialului este superior lui P. Solicitand materialul prin valori ale tensiunii pana la limita de elasticitate _e, materialul se comporta elastic, adica deformatiile dispar complet la incetarea actiunii sarcinilor. Daca tensiunile depasesc punctul E de pe curba, deformatiile nu mai sunt total elastice, adica total reversibile.

Peste _e materialul are o comportare elasto-plastica pana la rupere. In zona CD a curbei caracteristice, zona nu prea indepartata de limita de elasticitate, epruveta se lungeste fara a fi nevoie de o crestere a tensiunilor . Cand s-a ajuns in acest stadiu de solicitare, materialul se deformeaza mult sub sarcina constanta, semanand foarte mult cu curgerea lichidelor, de unde si denumirea de limita de curgere pentru tensiunile corespunzatoare stadiului respectiv de incarcare si de palier de curgere pentru portiunea respectiva a curbei caracteristice. Aceasta limita se noteaza prin _C. Pentru a avea o idee oricat de sumara asupra marimii deformatiilor la curgere, se precizeaza ca deformatia OD' este de circa 20 ori mai mare ca deformatia elastica OE'.

Dupa depasirea palierului de curgere, curba caracteristica prezinta o zona de intarire sau de autoconsolidare, cresterea deformatiilor in aceasta zona fiind legata de cresterea tensiunilor. Cand se atinge punctul maxim M se produce fenomenul de gatuire a epruvetei, iar in continuare deformatiile se concentreaza mai mult in zona gatuita, unde si eforturile unitare sunt mai mari ca urmare a micsorarii pronuntate a sectiunii.

Dupa punctul M, curba caracteristica are un traseu descendent pana la ruperea materialului marcata de punctul R. Vom face observatia importanta ca ceea ce s-a trasat in fig. 1.8 prin linie plina reprezinta curba caracteristica conventionala a materialului. Conventionala pentru ca tensiunile sunt obtinute considerand sectiunea transversala constanta a epruvetei pe timpul incercarii. In realitate aceasta sectiune se micsoreaza continuu pana la ruperea epruvetei. Fenomenul este cunoscut sub denumirea de contractie transversala.

Daca se traseaza o curba - ε, cu determinat pe baza sectiunii reale contractata a epruvetei, se obtine curba caracteristica reala a materialului, avand un traseu mereu ascendent, pana in punctul R' marcand ruperea reala. Curba caracteristica reala nu contine paradoxuri ca cea conventionala pentru care ruperea apare ca survenind la tensiuni mai mici decat tensiunile maxime. Curbele caracteristice conventionale se pot insa inregistra direct la masinile de incercat. Acesta este motivul pentru care ele sunt utilizate mult in rezistenta. In afara de aceasta, in calculele obisnuite de rezistenta curba caracteristica intereseaza numai pana la limita de curgere.

Ordonata maxima a curbei caracteristice - ε se numeste limita de rupere si se noteaza _r

Daca lungimea intre reperele de pe epruveta in momentul ruperii este l_r (lungirea care se poate masura dupa rupere prin alaturarea celor doua bucati de epruveta) se calculeaza lungirea specifica la rupere in felul urmator:

(1.15)

Obisnuit ea se reprezinta in procente, notandu-se

Gatuirea specifica la rupere se defineste prin raportul:

(1.16)

in care A_r reprezinta aria sectiunii gatuite a epruvetei masurata dupa rupere.

Marimile _{p e c r} d si y formeaza principalele caracteristici mecanice ale unui material.

Curba caracteristica prezentata, avand prima sa portiune rectilinie, descrisa de legea lui Hooke, apartine precum s-a spus, otelului moale. Materialele pentru care prima portiune a curbei caracteristice este o dreapta formeaza clasa materialelor care asculta de legea lui Hooke.

Materialele de acest fel sunt foarte putine. Majoritatea materialelor nu asculta de legea lui Hooke.Curbele lor caracteristice sunt reprezentate de expresii analitice de forma:

(1.17)

E₀ fiind o constanta si α un exponent cu valori supraunitare pentru unele materiale (fonta, alama, cupru, beton, cauciuc) si subunitare pentru altele (fibre textile, curea).

Fig. 1.9

Folosirea in calcule a unei relatii ca cea de mai sus in locul legii lui Hooke, fiind foarte dificila, se admite in mod conventional ca si aceste materiale asculta de legea lui Hooke; modulul de elasticitate se determina in acest caz aproximand cu o dreapta prima portiune a curbei caracteristice sau determinand unghiul de panta al curbei caracteristice in punctul corespunzator efortului unitar din piesa

(1.18)

Dupa cum s-a mai spus, depasirea limitei de elasticitate pentru un material inseamna solicitarea sa in domeniul plastic.

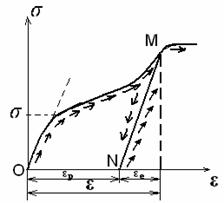
Fig. 1.10

Sa admitem ca un material este solicitat cum se arata in fig. 1.10 pana in punctul M al curbei sale caracteristice in domeniul plastic dupa care este descarcat complet.

Experienta arata ca descarcarea urmeaza o dreapta MN paralela cu dreapta reprezentand prima portiune a curbei caracteristice. Prin descarcare dispare numai deformatia elastica ε_e. Partea de deformatie care ramane ε_p dupa descarcare se numeste deformatie plastica.

In stadiul plastic de solicitare deformatia are deci doua componente, una elastica si una plastica.

(1.19)

Daca materialul descarcat este din nou solicitat ca la inceput, incarcarea va descrie dreapta NM a descarcarii, pastrand proportionalitatea intre tensiuni si deformatii pana in punctul M, superior limitei de proportionalitate a materialului. Prin urmare, prin solicitare in domeniul plastic si descarcare, se poate obtine cresterea limitei de proportionalitate si elasticitate pentru materiale. Tratamentul mecanic descris, prin care se obtine cresterea limitei de elasticitate se cheama ecruisare.

Practica arata ca materiale perfect elastice nu exista. Sub sarcini oricat de mici ele au anumite deformatii permanente. Urmare a acestui fapt se defineste drept limita de elasticitate tehnica _e valoarea tensiunii careia ii corespunde o alungire permanenta (dupa descarcarea epruvetei) de 0,01%.

Pentru materialele la care palierul de curgere lipseste din curba caracteristica, se defineste limita de curgere tehnica _c drept valoare a tensiunii careia ii corespunde dupa descarcarea epruvetei alungirea permanenta de 0,2%. In fig. 1.11, alungirea permanenta este data de segmentul OC'.

In afara de curba caracteristica pentru tensiunile normale, se poate construi pentru fiecare material si o curba caracteristica a tensiunilor tangentiale. Aceasta se obtine prin incercarea la rasucire a unei epruvete in forma de tub cu perete subtire si reprezinta legatura fizica intre tensiunile tangentiale τ si lunecarile specifice produse de ele. Se obtin pentru tensiunile tangentiale caracteristici mecanice ale materialului ca si pentru tensiunile normale: limita de proportionalitate, limita de elasticitate, de curgere, de rupere etc.

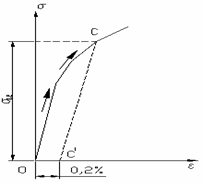
Fig. 1.11

Pentru otelul moale, pe prima portiune a sa, curba caracteristica este dreapta, materialul supunandu-se unei legi a lui Hooke pentru lunecare, (1.20)

G fiind modulul de elasticitate transversal, sau modulul de forfecare, cum se mai numeste.

Caracteristicile mecanice ale materialelor sunt functie de o serie de factori. Astfel temperatura influenteaza sensibil rezistenta de rupere care are un maxim pentru 200⁰ - 300⁰ C si coboara repede peste 400⁰ C. Modulul de elasticitate E, limitele de proportionalitate si curgere, scad continuu cu cresterea temperaturii. Lungirea la rupere si gatuirea la rupere prezinta un minim la 200⁰ - 300⁰ C dupa care cresc continuu cu temperatura. La temperaturi negative majoritatea materialelor tenace devin fragile, iar rezistentele la rupere cresc.

Viteza de aplicare a fortelor influenteaza mult caracteristicile mecanice ale materialelor. Astfel la viteze mari de aplicare a sarcinilor (socuri) materialele tenace se comporta ca materiale fragile, prezentand limite de rupere ridicate si lungiri la rupere foarte scazute.

Starea de tensiuni si de deformatii se modifica in timp indelungat. Fenomenul este cunoscut sub denumirea de fluaj.

1.7. Contractia transversala

Se constata pe baza de experienta ca odata cu lungirea barei sectiunea sa transversala se micsoreaza. Fenomenul se cheama contractie transversala. Raportul dintre scurtarea specifica a dimensiunilor transversale si lungirea specifica in sens longitudinal este coeficientul contractiei transversale m

(1.21)

Semnul minus s-a introdus prin faptul ca ε_t si ε sunt marimi de semne diferite. Inversul coeficientului m este coeficientul lui Poisson.

In urma contractiei transversale, o dimensiune transversala l_t a barei devine,

(1.22)

Aria A₀ a sectiunii transversale dupa contractie, cu neglijarea infinitului de ordinul doi m ε² devine,

(1.23)

Daca lungimea initiala a barei este l_o, dupa intindere aceasta devine

(1.24)

Volumul barei deformate va fi

Neglijand infinitul de ordin doi, 2mε², si avand in vedere ca A₀l₀ = V₀ rezulta,

(1.25)

Variatia de volum prin deformare va fi,

(1.26)

Pentru m=0,5 si V=0     bara se deformeaza fara variatie de volum. Aceasta proprietate o au insa numai lichidele. Experimental se constata ca in urma solicitarii volumul barei creste (DV>0) ceea ce implica m<0,5. Pentru metale s-a gasit pe cale experimentala m

Marimile E, G si m formeaza constantele elastice ale materialelor. Dupa cum se va vedea, numai doua dintre ele sunt independente.

1.8. Proprietatile mecanice ale materialelor

Insusirile materialelor descriind modul de comportare a lor sub actiunea sarcinilor formeaza ceea ce se numesc proprietatile mecanice ale materialelor.

Dupa reversibilitatea deformatiei materialele se pot clasifica in elastice, plastice si elasto-plastice. Un material este elastic daca dupa incetarea actiunii fortelor, deformatiile dispar complet. Materialele pentru care deformatiile se pastreaza integral dupa incetarea actiunii fortelor se numesc plastice. Daca dupa incetarea actiunii fortelor deformatiile dispar numai partial (o parte din ele pastrandu-se) materialul respectiv se va numi elastic-plastic. In natura toate materialele sunt de fapt elasto-plastice, apropiindu-se mai mult sau mai putin de cele plastice sau de cele elastice. Materialele perfect elastice sau perfect plastice nu se intalnesc niciodata in natura sau in tehnica. Notiunile de elastic si plastic sunt idealizari de care uzeaza stiintele pentru simplificarea calculelor lor.

Dupa marimea deformatiilor pana la rupere, materialele se pot clasifica in: tenace sau ductile si fragile sau casante. Sunt tenace acele materiale care prezinta deformatii mari pana la rupere si fragile acelea care se rup deformandu-se putin.

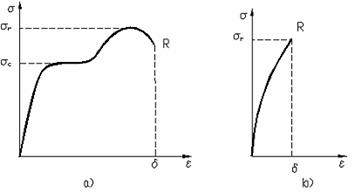
Fig. 1.12

Curbele caracteristice ale materialelor tenace si fragile sunt redate in fig. 1.12.a, respectiv fig. 1.12.b. Materialele tenace au o curba caracteristica mult alungita in directia axei si prezinta o limita de curgere s_c pronuntata si o alungire la rupere δ mare. Pentru materialele fragile curba caracteristica este scurta, alungirea la rupere mica, iar singura caracteristica mecanica ce se poate pune precis in evidenta este limita de rupere.

Din punct de vedere al unor constante fizice materialele se clasifica in omogene si neomogene. Sunt omogene acele materiale care au aceleasi constante fizice din toate punctele de vedere (structura, densitate etc.) Neomogene sunt materialele pentru care constantele fizice difera de la un punct la altul.

Dupa constantele elastice materialele se clasifica in materiale izotrope (aceleasi constante elastice dupa toate directiile) si materiale anizotrope (constante elastice diferite dupa directii diferite). In natura se intalnesc des materiale ortrotrope, adica materiale pentru care dupa doua directii perpendiculare constantele elastice nu variaza (lemn, laminatele prezentand structura fibroasa).

1.9. Conditii in problemele de rezistenta a materialelor

Pentru a-si putea indeplini rolul pentru care este conceputa , o piesa trebuie in general sa fie rezistenta , sa nu prezinte deformatii prea mari , iar configuratia sa geometrica sa nu se modifice sub actiunea solicitarilor .Toate acestea formeaza ceea ce se cheama in calculul de rezistenta conditii de rezistenta, de rigiditate si de stabilitate elastica .

Prin conditia de rezistenta calculul asigura ca intr-o sectiune a unei piese tensiunile sa fie mai mici decat cele admisibile (stabilite de practica sau impuse prin norme ).

Prin conditia de rigiditate calculul de rezistenta impune ca valorile deformatiilor intr-un anumit loc al piesei sa nu depaseasca pe cele admisibile

Prin conditia de stabilitate elastica , calculul de rezistenta impune pieselor solicitate ca echilibrul lor elastic sa fie stabil , trecerea de la pozitia de echilibru instabil la una de echilibru stabil , fiind legata de pierderea brusca a configuratiei geometrice , ceea ce compromite rolul functional al piesei pe de o parte si duce la aparitia de tensiuni suplimentare , pe de alta parte .

1.10. Ipoteze in teoria elasticitatii si rezistenta materialelor

Teoria elasticitatii si rezistenta materialelor, pentru a putea cuprinde din punct de vedere cantitativ in relatii matematice fenomene de solicitare a corpurilor deformabile , fac o serie de ipoteze simplificatoare asupra structurii si comportarii materialelor sub sarcini. Aceste ipoteze sunt de multe ori in concordanta cu realitatea , dar cateodata se abat mult de la aceasta . Deoarece rezultatele obtinute prin folosirea lor sunt verificate de experienta, inseamna ca ele sunt acceptabile pentru scopurile rezistentei materialelor si teoria elasticitatii. Aceste ipoteze sunt :

a) Ipoteza mediului continuu, conform cu care se admite ca materialele formeaza un mediu continuu si omogen umpland intregul spatiu ocupat de volumul lor . Evident ca aceasta ipoteza nu corespunde realitatii fizice , insa da posibilitatea folosirii in teoria elasticitatii si rezistenta materialelor a functiilor continui pentru descrierea variatiilor tensiunilor si deformatiilor. Ipoteza este mai apropiata de realitate pentru corpurile amorfe si mai indepartata pentru cele cristaline . Ea da posibilitatea sa se ocoleasca dificultatea luarii in seama a structurii atomo - moleculara a materiei.

b) Ipoteza izotropiei conform cu care materialele se considera izotrope , adica au in toate directiile aceleasi constante elastice . Exista si materiale anizotrope (constantele elastice variind cu directiile) pentru care ipoteza izotropiei nu mai este valabila.

c) Ipoteza elasticitatii perfecte, conform cu care admitem ca pana la anumite valori ale tensiunilor, materialele se comporta perfect elastic.

d) Ipoteza relatiei liniare intre tensiuni si deformatii specifice, conform cu care se admite ca in domeniul elastic tensiunile sunt proportionale cu deformatiile specifice (legea lui Hooke ). Consecinta acestei ipoteze este principiul suprapunerii efectelor :efectul unui grup de sarcini aplicat pe un corp deformabil este egal cu suma efectelor fiecarei sarcini aplicata separat pe corp .

e) Ipoteza deformatiilor mici. Cu unele exceptii, deformatiile corpurilor elastice sunt mici in raport cu dimensiunile lor. Aceasta permite ca in calcule, puterilor deformatiilor sa poata fi neglijate in raport cu puterea intaia a lor, iar ecuatiile de echilibru din mecanica sa poata fi scrise pentru corpul deformat la fel ca si pentru cel nedeformat .

f) Principiul lui Saint - Venant care se enunta astfel: sisteme de sarcini static echivalente actionand asupra unui element de suprafata a unui corp elastic produc la locul de aplicare tensiuni si deformatii ce se deosebesc apreciabil intre ele, dar aceste deosebiri sunt neinsemnate la distante mari de locul de aplicare a sarcini .

Pentru ilustrarea principiului se considera ca in fig 1.13. o bara incastrata la un capat intr-un masiv, iar la celalalt capat actionata de o forta F. Apoi aceiasi bara este actionata de aceiasi forta F dar distribuita pe o mica lungime .

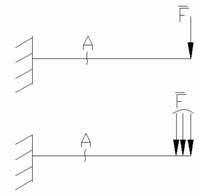
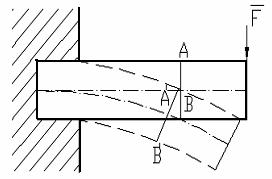
Fig. 1.13 Fig. 1.14

Conform principiului Saint-Venant la locul de aplicare a sarcinii , adica in capatul barei, tensiunile si deformatiile difera sensibil de la cazul intai la cazul al doilea, dar intr-o sectiune A indepartata de capatul barei tensiunile si deformatiile specifice sunt identice pentru ambele moduri de incarcare. Experienta confirma acest principiu.

g) Ipoteza lui Bernoulli sau ipoteza sectiunilor plane, conform cu care o sectiune plana normala pe axa barei inainte de deformare, ramane plana si normala pe axa si dupa deformare. Aceasta ipoteza, confirmata si de experienta, arata ca sectiunea plana AB a barei din fig 1.14., solicitata la incovoiere ramane tot plana si normala pe axa curba a barei dupa incovoiere. Ipoteza geometrica a lui Bernoulli este proprie numai rezistentei materialelor; teoria elasticitatii nu o foloseste .

1.11. Rezistente admisibile. Coeficienti de siguranta

In efectuarea calculelor de rezistenta se pune intrebarea fireasca, pana la care valoare a tensiunii vom admite sa fie solicitat materialul unei piese. Ca o prima orientare in acest sens trebuie sa ne serveasca faptul ca piesele nu numai ca nu trebuie sa se rupa in timpul functionarii, dar trebuie in general - sa aiba deformatii mici si cu caracter elastic. Prin urmare tensiunile nascute in piese nu trebuie sa depaseasca limita de elasticitate .

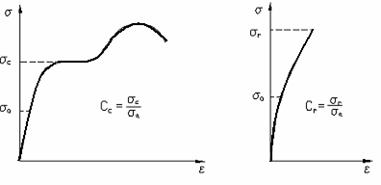
Fig. 1.15

Urmatoarele motive fac ca tensiunile din piese sa fie sub limita de elasticitate :

- determinarea sarcinilor este aproximativa si depasirea valorilor luate in calcul este posibila .

- schematizarea pieselor sub forma de bara, placa, schematizarea aplicarii sarcinilor si ipotezele de calcul reprezinta abateri fata de situatia reala .

- caracteristicile mecanice ale materialelor nu se pot determina cu precizie .

Valorile maxime ale tensiunilor (normale sau tangentiale) inferioare limitei de elasticitate care se admit in calcule pe baza practicii indelungate, formeaza ceea ce se cheama rezistente admisibile. Rezistentele admisibile sunt functie in primul rand de natura materialului si de felul solicitarii. Ele se noteaza cu σ_a si _a si se raporteaza de fapt, nu la limita de elasticitate, ci la una din valorile caracteristice distincte ale curbei caracteristice (superioara insa limitei de elasticitate) si reprezinta o fractiune din aceste valori. Astfel pentru materialele tenace care au o limita de curgere distincta σ_c si τ_c avem:

; (1.27)

iar pentru cele fragile , la care limita de curgere nu este definita , dar au o limita de rupere bine precizata,

;

Coeficientii c_c si c_r supraunitari se numesc coeficienti de siguranta .

In alegerea rezistentelor admisibile si a coeficientilor de siguranta trebuie sa se ia in considerare urmatorii factori:

- Natura materialului. Pentru fiecare material se poate trasa cate o curba caracteristica. Cu cat un material este mai neomogen cu atat mai mare trebuie sa fie coeficientul de siguranta si respectiv mai mica rezistenta admisibila.

- Tratamentele termice care modifica caracteristicile mecanice ale materialelor .

- Durata de folosire a piesei. Cu cat durata de functionare a piesei este mai mica, cu atat mai mici se pot lua coeficienti de siguranta, respectiv mai mari rezistentele admisibile.

- Modul de actionare in timp a sarcinilor. Pentru solicitarile variabile periodic (care duc la oboseala materialelor) coeficientii de siguranta difera de cei ai solicitarilor statice.

- Modul de evaluare a sarcinilor si de realizare a ipotezelor de calcul . Cu cat evaluarea sarcinilor este mai incerta si cu cat ipotezele de calcul se indeparteaza mai mult de realitate, cu atat coeficienti de siguranta trebuie sa fie mai mari .

- Felul solicitarii. Curbele caracteristice si respectiv caracteristicile mecanice ale materialelor, depind de felul solicitarii: intindere, compresiune, incovoiere, rasucire.

- Temperatura. Caracteristicile mecanice in functie de care se alege rezistenta admisibila sunt functie de temperatura .

Rezistentele admisibile se folosesc in mod diferit in calcule, dupa cum se face o dimensionare sau o verificare. In calculele de dimensionare se determina sectiunea transversala a pieselor astfel incat tensiunea maxima sa fie egala cu rezistenta admisibila.

In calculele de verificare se determina pe baza dimensiunilor efective ale piesei, tensiunea efectiva si se compara cu cea admisibila. Piesele se verifica numai daca prima tensiune este inferioara celei de a doua.

Dupa cum s-a aratat, rezistentele admisibile si coeficientii de siguranta nu sunt marimi pe care proiectantul sa le poata lua dupa voie, ci au valori precise, stabilite de practica indelungata ca fiind cele mai potrivite.