Analiza tensoriala

Analiza tensoriala

Generalitati

Marimile fizice din teoria fenomenelor de transfer pot fi clasificate in urmatoarele

categorii din punct de vedere tensorial:

scalari ( temperatura, energia, volumul, timpul, etc.);

vectori ( viteza, momentul, acceleratia,, forta, etc., )

tensori de ordinul doi ( tensorul eforturilor normale si tangentiale, viteza de

deformare prin forfecare, etc., )

Se disting urmatoarele notatii pentru marimile de mai sus:

s - scalar - tensor de ordinul zero;

vector - tensor de ordinul intai;

tensor - tensor de ordinul doi.

Sunt posibile cateva moduri de multiplicare a acestor marimi si se disting prin patru semne speciale: fara semn, un punct , doua puncte si cruce . Parantezele incluzand rezultatul multiplicarii indica tipul (ordinul tensorial ) al marimii rezultate, astfel: scalar, vector, tensor de ordinul doi sau mai mare.

Parantezele incluzand adunarea sau scaderea marimilor de mai sus nu au nici o semnificatie speciala, exemplu:

si se utilizaza dupa convenienta orice tip de paranteza.

.

De exemplu, numarul de componente al unei marimi scalare, pentru un spatiu tridimensional este: , numarul de componente al unei marimi vectoriale este , numarul de componente al unei marimi tensoriale de ordinul doi este: , s.a.m.d. Semnele de multiplicare se interpreteaza astfel:

in care reprezinta suma ordinelor cantitatilor care se multiplica.

Exemple:

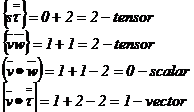
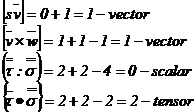
Operatii analitice cu vectori

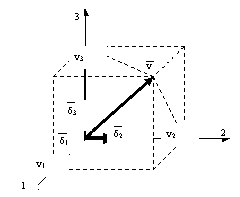
Pentru a caracteriza un vector din punct de vedere analitic trebuiesc cunoscute

componentele vectorului pe axele de coordonate carteziene: si versorii axelor de coordonate: ca in figura 1.

Fig.1.1. Proiectia unui vector pe axele de coordonate carteziene.

Operatorii ce intervin in operatiile cu vectori sunt:

simbolul Kronecker sau componentele tensorului unitar de ordinul doi:

simbolul permutarilor sau componentele tensorului de ordinul trei:

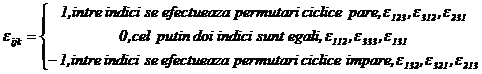
Tensorul permutarilor poate fi utilizat la dezvoltarea unui determinant de ordinul trei, deci un determinant de ordinul care poate fi scris sub urmatoarea forma in termeni de :

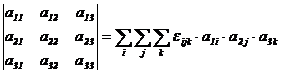
Simbolul selecteaza termenii din suma si determina semnul fiecarui termen din suma.

Multiplicarea a doua marimi tensoriale este echivalenta din punct de vedere tensorial cu multiplicarea versorilor si/sau diadelor.

Produsul simplu scalar a doi versori: .

Exemplu: ,

Produsul vectorial a doi versori: .

Exemplu: .

Definitia geometrica: - produsul simplu scalar este egal cu produsul marimilor

vectorilor care se multiplica si cosinusul unghiului intre cei doi vectori;

produsul vectorial este egal cu produsul marimilor vectorilor

care se multiplica , sinusul unghiului intre cei doi vectori si versorul perpendicular pe planul celor doi versori.

Operatori diferentiali vectoriali:

Se defineste operatorul diferential vectorial , nabla sau delta in coordonate carteziene, astfel:

Operatorul nabla aplicat unui scalar fara semn de multiplicare defineste un vector sau un gradient: , aplicat unui vector fara semn de multiplicare defineste o diada: si aplicat unui vector prin produs simplu scalar defineste un scalar: .

Operatori diferentiali scalari:

Se defineste operatorul diferential scalar , laplacianul in coordonate carteziene astfel:,

Se defineste operatorul diferential scalar , derivata substantiala sau de material in coordonate carteziene astfel: ,. Se aplica unui scalar sau unui vector.

Operatii analitice cu tensori

Un tensor de ordinul doi cu componentele se poate scrie

sub forma matriciala astfel:

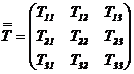
iar sub forma analitica: . Transpusa unui tensor de ordinul doi este:

.

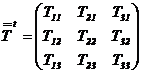Daca tensorul este simetric, ceea ce este echivalent cu . Produsul diadic a doi vectori si este o forma speciala a unui tensor de ordinul doi, in care elementele diadicului sunt similare componentelor tensorului:

.

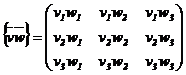Produsul diadic este anticomutativ .Tensorul unitate are componentele diagonalei principale si celelalte elemente nule:

.

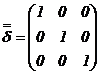Produsul diadic a doi vectori unitate are componenta si este de forma:

.

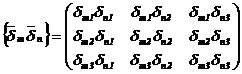Expresia analitica a produsului diadic este: .

Relatii intre versori si tensori unitate si intre tensori unitate utile in identificarea marimilor rezultate in operatiile de multiplicare:;

; ; .

Produsul diadic sau tensorial se mai poate nota astfel: . Urma unui tensor sau produs diadic ( in limba engleza trace cu simbolul , in limba germana spur cu simbolul ) are urmatoarea semnificatie ( transforma o diada sau un tensor de ordinul doi intr-un scalar echivalent cu suma elementelor de pe diagonala principala ):

; ;

.

Tensorul unitar de ordinul trei are expresia: .