Calculul practic de carene drepte. Metode numerice.

Calculul practic de carene drepte. Metode numerice.

Atat in timpul proiectarii navei, cat si in decursul exploatarii ei, apare necesitatea determinarii unor caracteristici cum sunt: arii, volume, momente de inertie, momente statice, etc. prezentate mai jos:

1. Aria plutirii (vezi formula 8.22)

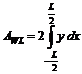
2. Ariile sectiunilor transversale (vezi formula 8.39)

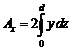
3. Volumul carenei (vezi formulele 8.2 si 8.3)

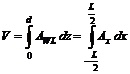
4. Momentele statice ale volumului carenei in raport cu planele sistemului de coordonate (vezi formulele 8.8 si 8.10)

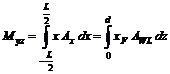
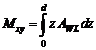
5. Momentul static al ariei plutirii (vezi formula 8.24)

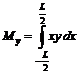
6. Momentele de inertie ale suprafetei plutirii (vezi formulele 8.26 si 8.27)

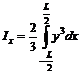
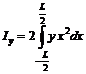
Determinarea acestor marimi implica rezolvarea unor integrale de forma:

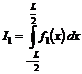sau .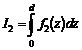

Daca functiile , respectiv ar fi cunoscute, atunci integralele si ar putea fi calculate analitic. Cum formele navei nu sunt date analitic, ele fiind definite discret, se apeleaza la integrarea numerica a integralelor si .

Principiul de integrare numerica se bazeaza pe faptul ca 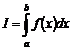reprezinta aria cuprinsa intre graficul functiei , axa si dreptele si .

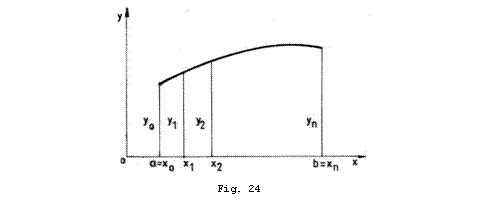
Valoarea aproximativa a integralei se obtine daca se divide intervalul in portiuni mai mici si apoi se insumeaza aria fiecarei fasii obtinute.

Formula generala de calcul a integralei printr-o metoda numerica este:

(9.1)

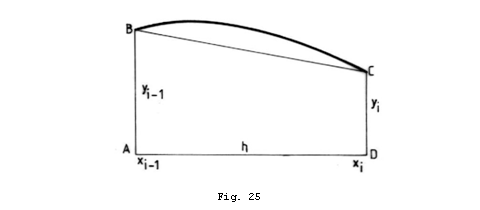
unde cu .

Daca presupunem curba de forma matematica polinom de gradul: atunci metodele de integrare numerica se pot clasifica dupa cum urmeaza:

1) metode in care intervalul se divide in parti egale avand capetele si iar problema este sa gasim coeficientii astfel incat relatia (9.1) sa exprime aria cautata (metoda trapezelor si metoda Simpson);

2) metode in care si problema consta in localizarea intervalelor din conditia de precizie maxima (metoda Cebasev);

3) metode in care problema consta atat in determinarea coeficientilor cat si in localizarea intervalelor din conditia de precizie maxima (metoda Gauss).

Metoda trapezelor

Aceasta metoda presupune ca poate inlocui curba dintre doua ordonate consecutive cu o dreapta de ecuatie (Fig. 25) si se poate aproxima aria patrulaterului curbiliniu cu aria trapezului avand valoarea :

Prin generalizare obtinem :

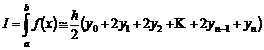(9.2)

unde .

Evident cu cat este mai mare, aproximarea integralei este mai buna. Un astfel de calcul se poate efectua si tabelar ca mai jos.

Metoda Simpson

In cadrul acestei metode se pastreaza principiul de la metoda trapezelor, insa aproximarea functiei de integrat pe portiuni nu se face prin segmente de dreapta, ci prin arce de parabola de gradul doi; (Fig. 26).

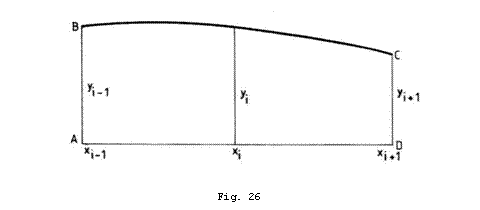
Cunoscand trei puncte consecutive prin care trece parabola se pot determina coeficientii ca solutii ale sistemului

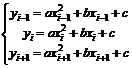(9.3)

Calculand acesti coeficienti si efectuand apoi integrarea obtinem pentru aria valoarea :

Prin generalizare obtinem :

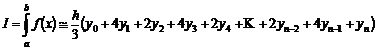(9.4)

sau :

(9.5)

unde :

;

;

.

O prima observatie care rezulta este ca numarul de intervale in care se divizeaza domeniul trebuie sa fie par.

Calculul se poate realiza tabelar dupa cum urmeaza :

Tabelul 5

Metoda Cebasev

Metoda Cebasev este foarte cunoscuta in domeniul naval fiind o varianta a metodei Gauss si care se bazeaza pe principiul intervalelor inegale dispuse in interiorul unui interval centrat fata de origine .

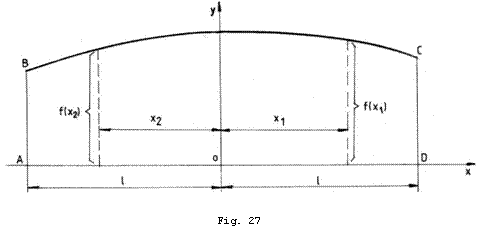
Conform cu figura 27 , aria este egala cu valoarea numerica a integralei .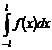

Daca presupunem ca are forma matematica a unui polinom de gradul :

(9.7)

atunci

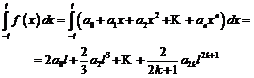(9.8)

unde sau dupa cum este par sau impar.

Pe de alta parte, acceptam pentru integrala de mai sus forma:

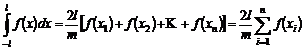(9.9)

unde si sunt necunoscutele problemei.

Dar

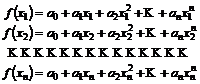(9.10)

Daca introducem (9.10) in (9.9) obtinem :

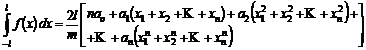(9.11)

Comparand relatiile (9.8) si (9.11) se obtine sistemul :

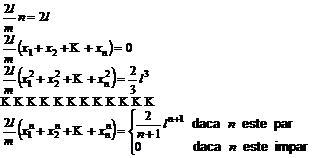(9.12)

Din prima conditie rezulta :

(9.13)

iar sunt solutiile sistemului :

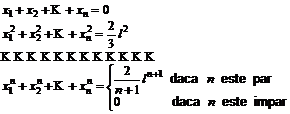(9.14)

Sa particularizam pentru cazul

si

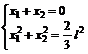(9.15)

Solutia acestui sistem este :

In consecinta

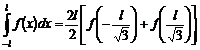(9.16)

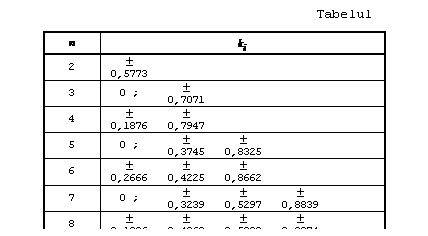
Similar se pot dezvolta formule pentru orice numar de termeni, coeficientii fiind prezentati in tabelul de mai jos.

Aplicarea metodei Cebasev presupune parcurgerea urmatorului algoritm :

- Se adopta numarul in functie de complexitatea curbei ;

- Se calculeaza abscisele cu relatia :

(9.17)

- Se extrag ;

- Se calculeaza valoarea integralei cu relatia:

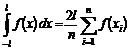(9.18)

In cazul integrarii numerice se poate apela cu succes la mijloacele automate de calcul putandu-se folosi programe specializate existente in acest scop.