 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Elemente de Statistica si Prelucrarea Datelor
Cerinta:
In sectiunea barata a unui curs de apa s-au inregistrat debitele medii lunare pe durata a 100 de ani de observatii, ca in tabelul de date primit pentru luna de analizat.
a) Sa se ordoneze crescator datele de esantion si sa se calculeze frecventa empirica folosind relatia
|
|
pentru data de rang r din sirul ordonat.
b) Sa se claseze datele intr-un numar convenabil de clase de ecart egal, calculand frecventele absoluta, relativa si cumulata.
c) Sa se reprezinte grafic histograma, frecventa relativa si frecventa cumulata.
d) Sa se calculeze statisticile de esantion (medie, mediana, moda, abaterea medie absoluta, varianta, abatere standard, coeficient de variatie, cuartile, coeficient de asimetrie, coeficient de boltire).
e) Presupunand ca lacul alimenteaza o
|
|
unde
![]() kg/m3, g =
9,81 m/s2, H (in m) sunt constante, Qi este debitul mediu
(m3/s) in clasa i, fi este frecventa relativa a clasei i, iar n
- numarul de clase.
kg/m3, g =
9,81 m/s2, H (in m) sunt constante, Qi este debitul mediu
(m3/s) in clasa i, fi este frecventa relativa a clasei i, iar n
- numarul de clase.
f) Admitand ca randamentul global pe amenajare este ![]() si ca intreg stocul
lunar afluent este uzinat, sa se afle productia
medie lunara de energie
si ca intreg stocul
lunar afluent este uzinat, sa se afle productia
medie lunara de energie
|
|
unde
z este numarul de zile ale lunii si sa
se gaseasca numarul mediu de ore de turbinare la debitul instalat ![]() mc/s.
mc/s.
g) Daca functia de densitate de probabilitate pentru debitul mediu lunar afluent este de tip Gamma cu 2 parametrii, adica
|
|
sa se gaseasca parametrii a si b
cu metoda
verosimilitatii maxime, unde ![]() este functia
este functia ![]() de parametru b
de parametru b
|
|
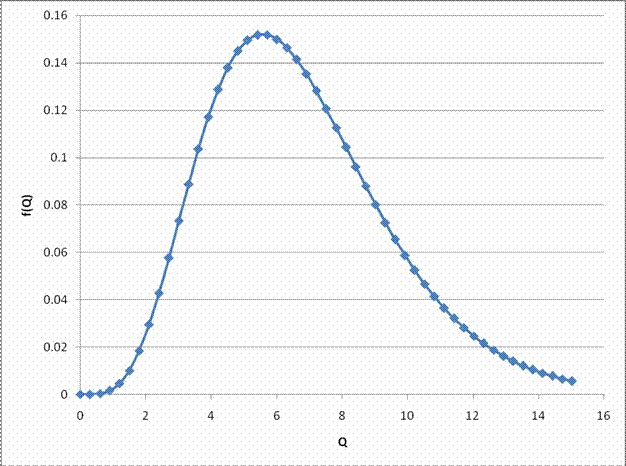
h) Sa se evalueze puterea hidraulica bruta lunara cu modelul probabilist
|
|
folosind functia de densitate f(Q) gasita anterior, precum si energia medie lunara corespunzatoare.
i) Utilizati testul hi - patrat pentru a verifica ipoteza nula ca functia de densitate gasita reda setul de date masurate, la nivel de semnificatie α = 0,005.
j) Care este riscul de respingere a lui H0, ea fiind adevarata ?
Rezolvare:
a) Operatiunea de ordonare a datelor de esantion se poate face in ordinea
crescatoare sau descrescatoare a valorilor lor numerice, in functie de scopul urmarit in analiza.
In proiect ordonarea s-a facut in ordine crescatoare, pentru a determina distributiile de frecventa de la subpunctele urmatoare.
Pentru calculul asigurarii empirice este necesara ordonarea lor descrescatoare
Numarul de ordine al unei date oarecare din sirul ordonat poarte denumirea de rang.
Cind doua date au valori identice, rangurile lor se precizeaza arbitrar fie la rangul mediu (identic pentru ambele), fie la rangul corespunzator ordinii initiale din seria originala.
Valoarea de rang r din sirul ordonat se va nota ![]() . Pentru un sir ordonat crescator
. Pentru un sir ordonat crescator ![]() =
= ![]() si
si ![]() =
= ![]() .
.
Prin ordonare apare una dintre caracteristicile descriptive ale seriei de date si anume plaja (sau domeniul) in care se plaseaza valorile ei.
La ordonarea crescatoare, aceasta rezulta egala cu ![]() .
.
Cu sirul de date ordonat crescator si ![]() valoarea
variabilei de rang r in sirul respectiv, exista diverse formule propuse pentru
a evalua ceea ce se numeste frecventa empirica (in fapt frecventa cumulata)
corespunzatoare valorii
valoarea
variabilei de rang r in sirul respectiv, exista diverse formule propuse pentru
a evalua ceea ce se numeste frecventa empirica (in fapt frecventa cumulata)
corespunzatoare valorii ![]() , care se pot
exprima prin relatia generala:
, care se pot
exprima prin relatia generala: ![]() .
.
Tabel 1. Datele de intrare (debitele masurate pe luna septembrie):
Tabel 2. Ordonarea crescatoare a debitelor si calculul frecventei empirice:
|
Rang |
Q[mc/s] |
F(xr) |
Rang |
Q[mc/s] |
F(xr) |
|
|
Rang |
Q[mc/s] |
F(xr) |
Rang |
Q[mc/s] |
F(xr) |
|
b) La alegerea numarului de clase, K, trebuie ca acesta sa nu fie prea mic (pierzand astfel multe informatii asupra formei distributiei), dar totusi suficient de mic pentru a permite o viziune sintetica asupra datelor analizate.
In functie de talia esantionului, se aleg intre 5 si 15 clase, dupa una din relatiile:
![]() sau
sau ![]()
Notand prin "k" indicele de clasa (k = l, 2,,K), apar urmatoarele definitii si relatii:
ecartul (sau amplitudinea) clasei hk ;
limita inferioara ak;
limita superioara bk si ![]()
valoarea centrala ck si ![]()
frecventa absoluta (numarul de aparitii) a clasei nk : 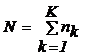
frecventa relativa a clasei f k : ![]()
frecventa cumulata pana la clasa k inclusiv Fk : 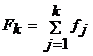 ,iar
,iar 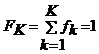 . Frecventele
se exprima uneori in procente.
. Frecventele
se exprima uneori in procente.
De regula se prefera gruparea in clase de ecart ![]() constant si avand
limitele de clasa alese cu valori convenabile (multiplii de 2, 5, 10, 100
etc.).
constant si avand
limitele de clasa alese cu valori convenabile (multiplii de 2, 5, 10, 100
etc.).
De asemenea limita inferioara ![]() si respectiv
superioara
si respectiv
superioara ![]() (pentru clasele
extreme) se fixeaza tinand seama:
(pentru clasele
extreme) se fixeaza tinand seama:
de valorile extreme din sirul ordonat crescator,
de numarul de clase K si
de ecartul ![]() rezultat.
rezultat.
In proiect numarul de clase s-a ales ca fiind egal cu 8, astfel:
s-a calculat plaja = xmax - xmin = Qmax - Qmin = 15,03-1,71 = 13,32
s-a calculat ecartul: ecart = plaja/k= 13,32/8 = 1,68
In tabelele urmatoare se prezinta datele calculate la punctual b astfel:
o tabel cu determinarea numarului de clase de ecart egale, limita inferioara si limita superioara fiecarei clase.
a1 = Qmin-0,07; b1 = a1 + ecart
a2 = b1; b2= a2 + ecart
o tabel cu determinarea frecventei absolute, relative si cumulate.
Tabel 3. Determinarea plajei
|
k | |
|
plaja | |
|
ecart |
Tabel 4. Determinarea numarului de clase de ecart egale
|
Interval |
ai |
bi |
ci |
|
nr. |
[m3/s] |
[m3/s] |
[m3/s] |
Tabel 5. Determinarea frecventelor cumulate, relative si absolute:
|
Interval |
ai |
bi |
ci |
ci |
nk |
fk |
Fk |
|
nr. |
[m3/s] |
[m3/s] |
[m3/s] |
[m3/s] | |||
|
| |||||||
c) Reprezentarea tabelara a distributiei de frecventa este utila pentru identificarea caracteristicilor unei colectii mari de date, dar adesea se prefera evidentierea acestor caracteristici prin reprezentari grafice.
Exista doua categorii importante de grafice si anume:
o histogramele - realizate prin construirea unor dreptunghiuri succesive;
o poligoanele - care se obtin unind puncte succesive prin segmente de linii drepte.
In cazul histogramelor, pe abcisa se reprezinta plaja de valori in care se incadreaza datele din sir, iar pe ordonata apare fie frecventa absoluta (numarul de aparitii) din fiecare clasa, fie frecventa relativa (normalizata sau exprimata in procente).
Ca regula generala , suprafata dreptunghiului corespunzator fiecarei clase trebuie sa fie proportionala cu efectivul (sau frecventa) ei. Din acest motiv la clasarea cu h constant, inaltimile dreptunghiurilor din histograma vor fi proportionale cu frecventele claselor.
In continuare sunt prezentate graficele frecventelor cumulate, absolute si relative, histograma cu clase de ecart egale si tabelele cu marimile necesare reprezentarilor grafice.
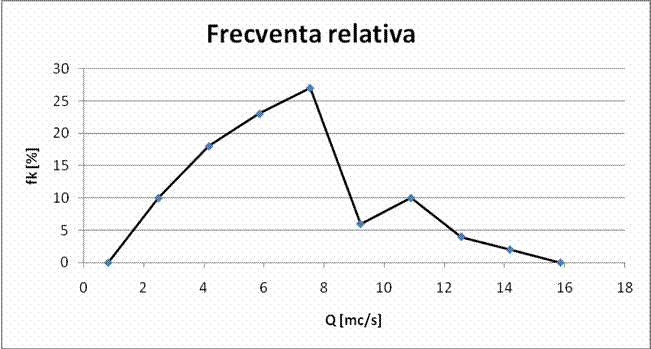
Fig 1. Graficul frecventei relative
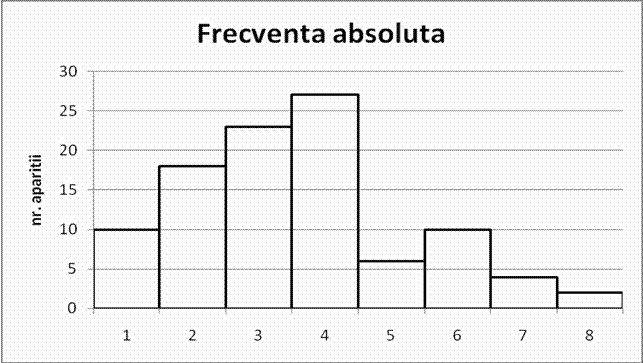
Fig 2. Graficul frecventei absolute ( histograma)
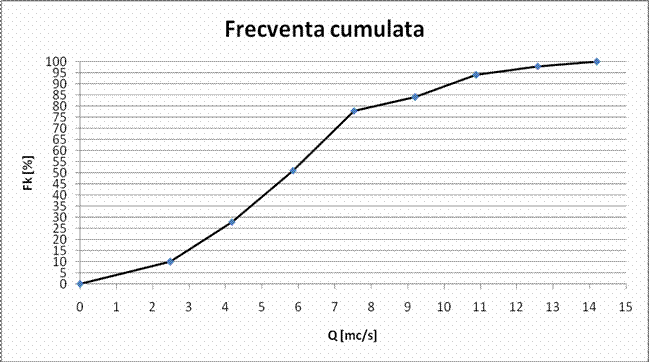
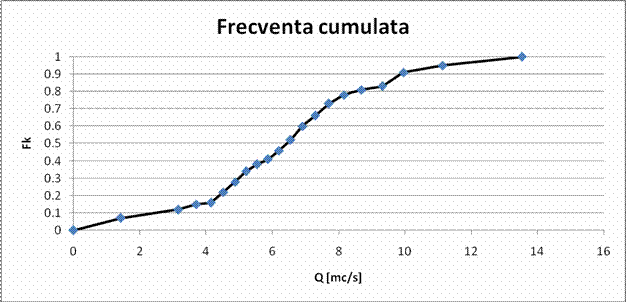
Fig. 3. Graficul frecventei cumulate
d) Masuri ale tendintei (pozitiei) centrale:
Media aritmetica (numita prescurtat media) unui set de date ![]() se noteaza cu
se noteaza cu ![]() si este data de:
si este data de:
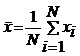 .
.
Mediana - notata ![]() - este definita
ca valoarea fata de care jumatate dintre observatiile seriei de date sunt mai
mari si respectiv cealalta jumatate sunt mai mici.
- este definita
ca valoarea fata de care jumatate dintre observatiile seriei de date sunt mai
mari si respectiv cealalta jumatate sunt mai mici.
Se mai numeste si valoare echiprobabila sau cuartila de ordin 2.
Pentru un sir de date ordonate:
daca talia sirului N este numar impar, atunci mediana va fi egala cu data
de rang ![]() , adica:
, adica: 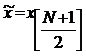
iar daca N este numar par, mediana se admite egala cu media datelor de
ranguri N/2si respectiv N/2+1, adica: ![]()
Moda - notata ![]() - se defineste ca
fiind valoarea care apare cel mai frecvent printre datele observate.
- se defineste ca
fiind valoarea care apare cel mai frecvent printre datele observate.
Se mai numeste si valoare dominanta, valoarea cea mai probabila sau valoare modala.
Moda poate sa nu fie unica intr-un set de date observate sau chiar poate sa nu existe.
Distributiile care au o singura valoare modala (cea mai frecventa) se numesc unimodale.
Daca insa doua valori numerice diferite se regasesc de acelasi numar de ori (cel mai mare) printre observatiile din set, este vorba despre o distributie bimodala.
Cand toate datele observate sunt diferite intre ele, in mod evident moda nu poate fi definita.
Daca setul de observatii este grupat pe clase, atunci se vorbeste de una sau mai multe clase modale.
Relatia intre medie, mediana si moda
Se presupune ca:
numarul de date din sir, N, este foarte mare
a fost posibila o clasare cu
ecart ![]() foarte mic (astfel incat poligonul
frecventelor poate fi aproximat printr-o curba continua si unimodala) relatia intre
foarte mic (astfel incat poligonul
frecventelor poate fi aproximat printr-o curba continua si unimodala) relatia intre
![]()
![]() si
si ![]() depinde de alura
distributiei de frecventa.
depinde de alura
distributiei de frecventa.
a. 
b. 
c.

Pentru oricare dintre tipurile de distributie
a), b) sau c) mediana ![]() este plasata
astfel incat verticala prin
este plasata
astfel incat verticala prin ![]() imparte suprafata
de sub graficul de frecventa in doua parti de suprafete egale (A1 =
A2).
imparte suprafata
de sub graficul de frecventa in doua parti de suprafete egale (A1 =
A2).
Moda ![]() corespunde
abscisei pentru care frecventa relativa inregistreaza un maxim.
corespunde
abscisei pentru care frecventa relativa inregistreaza un maxim.
Cu aceste precizari:
pentru cazul a): ![]() <
<![]() <
<![]() si se spune
ca distributia are asimetrie pozitiva;
si se spune
ca distributia are asimetrie pozitiva;
pentru cazul b): ![]()
![]()
![]() si se spune
ca distributia este simetrica;
si se spune
ca distributia este simetrica;
pentru cazul c): ![]() >
>![]() >
>![]() si se spune
ca distributia are asimetrie negativa.
si se spune
ca distributia are asimetrie negativa.
Abaterea medie absoluta - notata AMA- este definita ca media diferentelor absolute dintre fiecare
data a sirului si media lui, adica: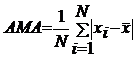
Varianta - notata ![]() - este definita
ca media patratelor diferentelor dintre fiecare data a sirului si media lui,
adica:
- este definita
ca media patratelor diferentelor dintre fiecare data a sirului si media lui,
adica: 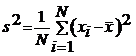
Abaterea standard (sau abaterea patratica medie sau abaterea tip) se noteaza cu s si este
egala cu radacina patrata din varianta, adica: 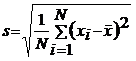
Deoarece abaterea standard are aceeasi dimensiune ca si variabila observata, ea este mult mai utila in practica in raport cu varianta si reprezinta caracteristica de dispersie cea mai sugestiva.
Coeficientul de variatie - notat cu ![]() - este definit ca raportul dintre abaterea
standard si media sirului, adica:
- este definit ca raportul dintre abaterea
standard si media sirului, adica: 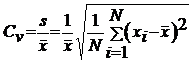
Este o caracteristica adimensionala si poate fi utilizat la comparatii efectuate asupra unor serii diferite de date.
Intervalele intercuantile:
Se numesc cuantile de ordin k - cele k-1 valori care impart datele seriei in k clase de aceeasi frecventa (clase echiprobabile).
Cele 99 percentile ![]() impart seria in 100
clase de efectiv N/100
impart seria in 100
clase de efectiv N/100
Cele 9 decile ![]() impart seria in 10 clase de efectiv
N/10
impart seria in 10 clase de efectiv
N/10
Cele 3 cuartile ![]() si
si ![]() impart seria in 4 clase de efectiv N/4
impart seria in 4 clase de efectiv N/4
De regula, cuantilelele se estimeaza pe baza ogivei frecventelor cumulate (cum s-a explicat in legatura cu mediana - care este in fond cuartila de ordinul doi).
Intervalul intercuartile se obtine ca diferenta ![]() si este o masura a dispersiei mai putin sensibila la
fluctuatiile de esantion decat amplitudinea (sau plaja).
si este o masura a dispersiei mai putin sensibila la
fluctuatiile de esantion decat amplitudinea (sau plaja).
Semnificatia percentilei ![]() - reprezinta valoarea sub care se plaseaza 70% dintre
datele observate.
- reprezinta valoarea sub care se plaseaza 70% dintre
datele observate.
Decila ![]() este valoarea
sub care se plaseaza 40% dintre datele sirului, iar cuartila
este valoarea
sub care se plaseaza 40% dintre datele sirului, iar cuartila ![]() corespunde
valorii sub care se regasesc 25% dintre date.
corespunde
valorii sub care se regasesc 25% dintre date.
Caracteristica de asimetrie a unei distributii
de frecventa se evalueaza prin coeficientul de asimetrie propus de
Fisher: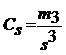
Se mai poate
scrie si: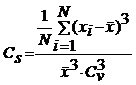 , iar daca se adimensionalizeaza datele seriei in
raport cu media si se introduce variabila modul
, iar daca se adimensionalizeaza datele seriei in
raport cu media si se introduce variabila modul ![]() , i=1,
2, . .N, atunci
, i=1,
2, . .N, atunci ![]() devine:
devine: 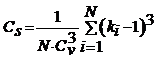 .
.
Alta masura a asimetriei, propusa de Pearson, este coeficientul
Pearsonian de asimetrie dat de:![]()
iar Yule propune coeficientul cuartil de simetrie
definit prin: 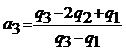 in care evident
in care evident ![]() .
.
Coeficientii ![]() si
si ![]() sunt mai putin
sensibili la fluctuatii de esantion.
sunt mai putin
sensibili la fluctuatii de esantion.
O alta caracteristica de forma se refera la boltirea (sau aplatisarea) graficului distributiei de frecventa.
Dupa Pearson coeficientul de boltire este definit
prin : 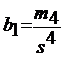 ,iar dupa Fisher prin relatia:
,iar dupa Fisher prin relatia: ![]() , in care
, in care ![]() pentru distributia
normala (se va detalia in alt capitol).
pentru distributia
normala (se va detalia in alt capitol).
Pentru aceeasi caracteristica, Kelly propune un coeficient
calculat pe baza cuartilelor, cu relatia: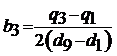 , unde d1 si d9 sunt decilele corespunzatoare.
, unde d1 si d9 sunt decilele corespunzatoare.
Tabel 6. Calculul statisticilor de esantion
|
Media aritmetica | |||
|
Mediana | |||
|
Moda | |||
|
AMA | |||
|
Varianta | |||
|
Abaterea standard | |||
|
Coef. de variatie | |||
|
q1 | |||
|
q2 | |||
|
q3 | |||
|
m3 | |||
|
s^3 | |||
|
Cs |
asimetrie Fisher |
||
|
a2 |
asimetrie Pearson |
||
|
a3 |
asimetrie Yule |
||
|
m4 | |||
|
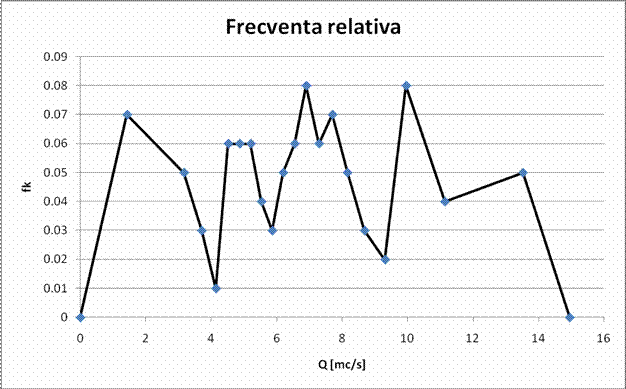
b1 |
boltire Pearson |
||
|
b2 |
boltire Fisher |
||
e) Se doreste determinarea puterii brute lunare empirice, pentu o cadere H= 465m.
Puterea bruta se
calculeaza cu realatia: P = ![]() [mw], unde:
[mw], unde:
P - puterea ce se doreste a fi determinate [MW]
ρ - densitatea apei [kg/mc]
H - inaltimea bruta [m]
Qi - debitul mediu calculate pe fiecare clasa de ecart
g - accelearatia gravitational [m/s2]
n - numarul de clase.
Tabel 7. Debitele medii calculate pe fiecare clasa de ecart si puterea bruta lunara
|
Interval |
ci |
P |
|
nr. |
[m3/s] |
[MW] |
P = 31,0484 [MW]
f) Se cere determinarea productie medie de energie lunara pentru un randament η= 88%, in conditia turbinarii totale a debitului mediu afluent.
E = 24ZPη [MWh], unde:
E - energia [MWh]
Z - numarul de zile din luna de calcul (30 - luna septembrie)
P - puterea determinata la punctul anterior [MW]
η - randamentul global [%].
E = 19672,28 [MWh]
Se mai cere sa se gaseasca numarul de ore mediu de turbinare pentru un debit instalat Qinst = 40 [m3/s].
t = (24 * Z * Qafl)/Qinst;
Qafl = (ci*fk)/100 ;
|
Interval |
ci |
fk |
Qafl |
|
nr. |
[m3/s] |
[m3/s] |
|
t = (24*30*6,8064)/40 = 122,5152 ore
g)
Metoda verosimilitati maxime: este una dintre cele mai frecvent folosite
metode de estimare a parametrilor ![]() ai unei legi de
probabilitate de forma generala
ai unei legi de
probabilitate de forma generala ![]() , pornind de la observatiile unui esantion de n valori
, pornind de la observatiile unui esantion de n valori ![]() care sunt realizari
ale V.A. X si pentru care se urmareste particularizarea expresiei lui
care sunt realizari
ale V.A. X si pentru care se urmareste particularizarea expresiei lui ![]() .
.
Se numeste functie de verosimilitate si se noteaza prin L produsul:
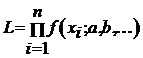 , care reprezinta
densitatea de repartitie comuna a variabilelor de selectie.
, care reprezinta
densitatea de repartitie comuna a variabilelor de selectie.
Exemple de aplicare a metodei verosimilitatii maxime:
Legea Poisson
Legea binomiala
Legea de distributie normala
Legea log-normala de parametri a si b cu functia de densitate:
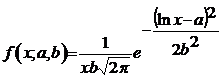 ,procedand
ca mai sus, se gasesc estimatorii de verosimilitate maxima:
,procedand
ca mai sus, se gasesc estimatorii de verosimilitate maxima: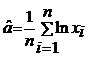 si
si 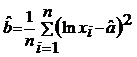
In cadrul prezentului proiect s-a utilizat pentru rezolvarea acestei cerinte un limbaj de programare ( Turbo Pascal) cu care s-au aflat cei doi parametri "a" si "b".
a = 0,839
b = 5,675
Tabel 8. Calculul functiei de densitate de probabilitate
|
Q |
f(Q) |
Q |
f(Q) |
|
|
| ||||
h) Se cere determinarea puterii hidraulice brute si energiei medii corespunzatoare folosind functia de densitate f(Q) determinata la punctul "g".
P = 10-6 ρgQH![]() ∙f(Q)∙dQ
∙f(Q)∙dQ
Determinarea puterii si a energiei brute s-a realizat tot cu ajutorul limbajului de programare Turbo Pascal, folosindu-ne de parametrii "a" si "b" obtinuti anterior.
Astfel a rezultat:
Pb = 30,86 MW
n = 30 zile
El = 19549,74 MWh
|
Interval |
ai |
bi |
ci |
fr |
ft |
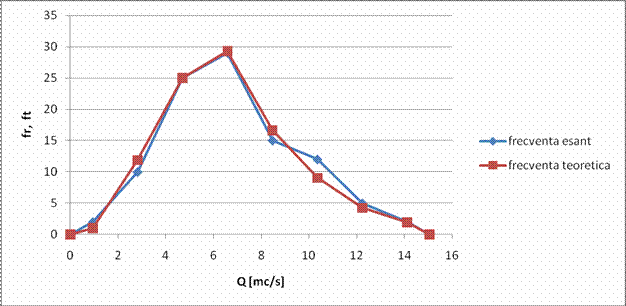
i) Testul hi-patrat - se poate aplica atat V.A. continue, cat si discrete, fiind adecvat in urmatoarele situatii:
Cand ipoteza nula precizeaza complet legea teoretica de probabilitate si se compara frecventele cumulate observate cu cele date de modelul teoretic (utilizare ca test de conformitate);
Cand ipoteza nula precizeaza doar forma
legii teoretice in timp ce estimarile parametrilor ei trebuie obtinute separat, atat pentru executarea
testului, cat si pentru utilizarea ulterioara a distributiei, daca ![]() este acceptata
(test de ajustare sau de concordanta).
este acceptata
(test de ajustare sau de concordanta).
Dezavantajul lui major - pentru a fi edificator este necesar ca talia N a esantionului de date observate sa fie suficient de mare.
Principiul testului se bazeaza pe
comparatia, pentru o clasa data de valori, a numarului de aparitii observate, ![]() , cu numarul de aparitii corespunzator functiei
teoretice testate, pentru clasa respectiva, notat
, cu numarul de aparitii corespunzator functiei
teoretice testate, pentru clasa respectiva, notat ![]() .
.
In cadrul lui se verifica daca suma patratelor diferentelor dintre ![]() si
si ![]() ramane in limite
rezonabile, de ordinul de marime al fluctuatiilor de esantionare
plauzibile.Pentru N suficient de mare, estimatorul de test notat prin
ramane in limite
rezonabile, de ordinul de marime al fluctuatiilor de esantionare
plauzibile.Pentru N suficient de mare, estimatorul de test notat prin ![]() si dat de relatia:
si dat de relatia: 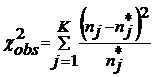 este o V.A. de lege
este o V.A. de lege ![]() cu
cu ![]() grade de
libertate, K fiind numarul de clase utilizate in testare.
grade de
libertate, K fiind numarul de clase utilizate in testare.
Numarul gradelor de libertate,![]() , depinde de tipul testului:
, depinde de tipul testului:
Daca
valorile parametrilor ![]() ai legii
teoretice
ai legii
teoretice ![]() sunt cunoscute cu
precizie (test de conformitate), atunci
sunt cunoscute cu
precizie (test de conformitate), atunci ![]() .
.
Daca
se folosesc estimari ![]() ale parametrilor
(test de concordanta), atunci
ale parametrilor
(test de concordanta), atunci ![]() , cu p - numarul de parametri.
, cu p - numarul de parametri.
Puterea testului este maxima daca numerele de aparitie teoretice, ![]() sunt egale
pentru toate clasele si, in plus,
sunt egale
pentru toate clasele si, in plus, ![]() .
.
Pasii concreti ai procedurii de testare sunt urmatorii:
efectiv) prin ![]() ;
;
cu
relatia ![]() . In acest caz, expresia lui
. In acest caz, expresia lui ![]() se modifica de
la forma (8.1) la
se modifica de
la forma (8.1) la
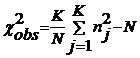 ,
,
domeniul
pe care se intind datele de esantion. De ex. - ![]() , pentru
, pentru ![]() , vor fi cuantilele
, vor fi cuantilele ![]() pentru care
pentru care ![]() . Evident ca
. Evident ca 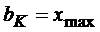 , iar
, iar ![]() si
si ![]() , cu
, cu ![]() si
si ![]() valorile extreme
din setul de date observate;
valorile extreme
din setul de date observate;
clasa
si se calculeaza ![]() cu relatia
(8.3);
cu relatia
(8.3);
tipul testului;
Se calculeaza cuantila ![]() pentru nivelul
de semnificatie α ales sau se calculeaza probabilitatea critica
pentru nivelul
de semnificatie α ales sau se calculeaza probabilitatea critica ![]() - egala cu
riscul de a gresi prin respingerea ipotezei nule
- egala cu
riscul de a gresi prin respingerea ipotezei nule ![]() .
.
Programul Test_hi2 efectueza testul de concordanta pentru legi teoretice cu
doi parametri - de forma generala ![]() - si anume:
legea normala
- si anume:
legea normala ![]() , legea log-normala
, legea log-normala ![]() , legea Gamma
, legea Gamma ![]() si legea Weibull
si legea Weibull
![]() .
.
Testul hi-patrat se poate aplica si folosind clase de ecart egal dupa X , in
locul claselor echiprobabile ca frecventa. In programul Test_hi2 nu se prevede
aceasta varianta (gasirea valorii
numerice a lui ![]() fiind mai
complicata).
fiind mai
complicata).
Procedura de testare hi-patrat se poate folosi si pentru a testa ipoteza independentei a doua variabile aleatoare.
Pentru efectuarea testului se aleg esantioane aleatoare independente de
talii ![]() din cele k populatii si se aranjeaza datele ca frecvente
observate.
din cele k populatii si se aranjeaza datele ca frecvente
observate.
In proiectul nostru verificarea cu testul hi-patrat se face cu ajutorul limbajului de programare Turbo Pascal.
Tabel 9. Limite de clase si numar de aparitii
|
clasa |
ai = xinf |
b = xsup |
ci |
nk |
fk |
Fk |
j) Pentru pragul α = 0,05, a rezultat cu ajutorul programului de calcul Turbo Pascal
Hiobs= 14
Hicrit = 27,588
Asadar ipoteza se accepta.
Risc asumat daca refuz Ho: 66.71 %
Copyright © 2025 - Toate drepturile rezervate
| Statistica | |||
|
|||
|
| |||
|
| |||
|
|
|||