 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
CORELATIA SI REGRESIA STATISTICA
Prin corelatie statistica se intelege intensitatea si directia legaturii statistice dintre doua sau mai multe variabile. Este important de retinut faptul ca legatura sau corelatia statistica dintre doua sau mai multe variabile nu implica necesar si legatura cauzala dintre acestea.
Karl Pearson a propus ca statistica de masurare a intensitatii si directiei legaturii statistice liniare dintre doua variabile coefcientul care-i poarta numele, definit ca raport intre covarianta statistica si produsul abaterilor standard ale variabilelor studiate:
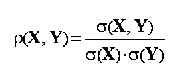
unde (X, Y) reprezinta coeficientul de corelatie liniara Pearson;
(X, Y) = covarianta statistica a variabilelor X si Y;
(X), (Y) = abaterile standard ale variabilelor X si Y.
Proprietati ale coeficientului de corelatie liniara Pearson
coeficientul de corelatie liniara Pearson poate inregistra valori cuprinse intre -1 si +1. Intrucat abaterile standard nu pot fi negative, inseamna ca semnul coeficientului de corelatie liniara Pearson este dat de semnul covariantei. Deoarece covarianta este pozitiva atunci cand predomina tendinta de variatie in acelasi sens pentru variabilele studiate, inseamna ca o valoare pozitiva a coeficientului de corelatie liniara Pearson indica o corelatie statistica directa intre variabile. Invers, intrucat covarianta este negativa atunci cand predomina tendinta de variatie in sensuri opuse pentru variabilele studiate, inseamna ca o valoare negativa a coeficientului de corelatie liniara Pearson indica o corelatie statistica inversa intre variabile;
coeficientul de corelatie liniara Pearson dintre o variabila X si o variabila constanta este egal cu 0:
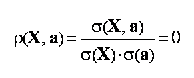
unde a este o variabila constanta;
daca intre doua variabile exista o legatura functionala liniara, atunci coeficientul de corelatie liniara Pearson inregistreaza valorile ±1:
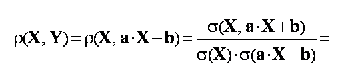
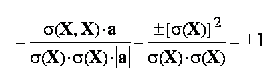
unde ecuatia Y = a·X + b exprima legatura liniara functionala dintre variabilele X si Y (a, b = constantele care definesc legatura liniara functionala);
coeficientul de corelatie liniara Pearson este comutativ:
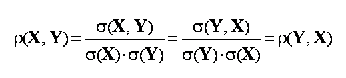
unde X, Y sunt variabile statistice;
adaugarea sau scaderea unei constante la toate valorile inregistrate de o variabila X nu determina modificarea coeficientului de corelatie liniara Pearson dintre variabila X si o alta variabila Y:
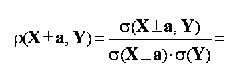
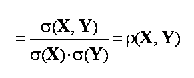
unde a reprezinta o constanta;
multiplicarea sau impartirea cu o constanta a tuturor valorilor inregistrate de o variabila X nu determina modificarea coeficientului de corelatie liniara Pearson dintre variabila X si o alta variabila Y:
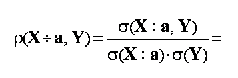
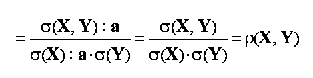
unde a reprezinta o constanta;
coeficientul de corelatie liniara Pearson este invariant la schimbarea originii si a unitatii de scara (a se vedea si figura 6.1.):
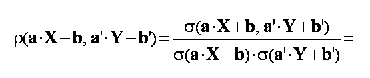
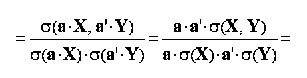
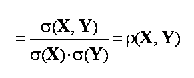
Sa consideram, de exemplu, variabilele X si Y din tabelul 6.1.
Tabelul 6.1.
|
X |
Y |
Alegand parametrii a = 2,3; b = 5; a' = 7 si b' = 3,4 se obtin valorile din tabelul 6.2., reprezentate grafic in figura 6.1.
Tabelul 6.2.
|
X |
Y |
a'Y+b' |
|
|
|
|||
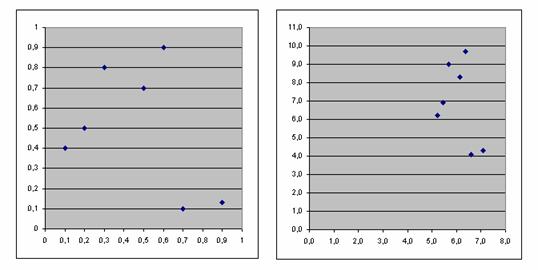
Figura 6.1.
Asa cum se observa si in figura 6.1., pentru cele doua perechi de variabile corelatia este identica. Identitatea se mentine si in ce priveste coeficientul de corelatie liniara Pearson:
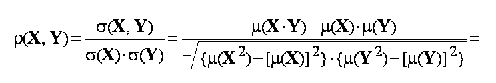
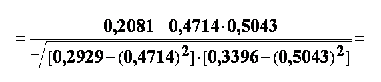
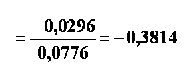
respectiv,
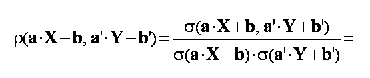
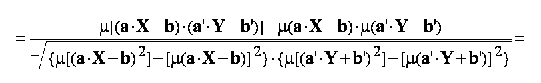
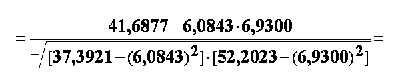
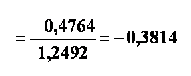
Regresia statistica este folosita pentru modelarea legaturilor statistice dintre variabile. Modelele construite prin regresie pot fi folosite apoi la realizarea de predictii statistice.
Prin regresia statistica se modeleaza legaturile statistice dintre una sau mai multe variabile endogene (denumite si variabile prezise, explicate sau dependente, si notate uzual cu Y) si una sau mai multe variabile exogene (denumite si variabile predictoare, explicative sau independente, si notate uzual cu X).
Tipuri de regresie statistica
Pentru regresia statistica sunt disponibile modele liniare, construite pe baza unor ecuatii sau functii matematice liniare, si modele neliniare, construite pe baza unor ecuatii sau functii matematice neliniare.
Modelele construite cu o singura variabila explicate sunt modele de regresie univariata, iar modelele construite cu mai multe variabile explicate sunt modele de regresie multivariata. Modelele de regresie univariata pot fi, la randul lor, modele de regresie simpla, construite pentru o singura variabila explicativa, si modele de regresie multipla, care implica mai multe variabile explicative in relatie cu variabila explicata considerata.
In afara acestor modele de regresie statistica, sunt disponibile si alte modele speciale, dintre care amintim modelul regresiei Poisson, modelul invatarii supervizate etc.
Erorile si valorile reziduale de regresie
Eroarea statistica de regresie pentru o anumita unitate statistica extrasa aleator din populatia statistica studiata, consta in abaterea valorii observate pentru aceasta unitate statistica de la valoarea asteptata conform modelului de regresie care s-ar aplica la nivelul intregii populatii statistice studiate. Atunci cand este observabil doar un esantion din populatia statistica studiata[1], aceste erori vor putea fi doar estimate.
Erorile
statistice de regresie pot fi confundate usor cu valorile estimate ale
lor, denumite valori reziduale de regresie. Acestea din urma sunt abateri
ale valorilor observate de la valorile asteptate conform modelului de
regresie aplicat doar la nivelul unui esantion observabil din populatia
statistica studiata. Cu alte cuvinte, valorile reziduale de regresie
sunt estimarile observabile (simbolizate obisnuit cu ![]() ) ale erorilor statistice de regresie
(simbolizate obisnuit cu ).
) ale erorilor statistice de regresie
(simbolizate obisnuit cu ).
Regresia liniara simpla pe baza metodei celor mai mici patrate; coeficientul de regresie liniara
Regresia liniara se numeste asa intrucat ea are la baza ipoteza ca raspunsul variabilei explicate la variabila explicativa imbraca forma unei functii liniare cu anumiti parametri. Deseori se considera, in mod eronat, ca motivul pentru care regresia se numeste "liniara" consta in faptul ca graficul functiei variabilei explicate, Y = + ·X, este o linie. De fapt, si in anumite situatii in care modelul este, din punct de vedere grafic, neliniar, regresia se poate reduce tot la un model liniar. Astfel, de exemplu, modelul Y = + ·X + ·X2 poate fi considerat un model liniar (de regresie multipla) in care Y este variabila endogena iar X2 si X sunt variabilele exogene.
Metoda celor mai mici patrate consta in minimizarea sumei patratelor abaterilor de regresie. Abaterile de regresie sunt abateri ale valorilor reale ale variabilei explicate (Y) de la valorile teoretice, calculate pe baza modelului de regresie liniara (Yc) aplicat la nivelul esantionului observat. Ele pot lua forma fie a erorilor statistice de regresie (daca sunt observabile toate raspunsurile variabilei explicate la variabila explicative), fie a valorilor reziduale de regresie (daca nu sunt observabile toate raspunsurile variabilei explicate la variabila explicative, regresia fiind aplicata doar la nivelul unui esantion de observatii).
Inainte de minimizarea sumei patratelor erorilor statistice de regresie este utila observarea urmatoarelor echivalente:
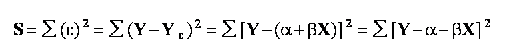
unde reprezinta erorile statistice de regresie;
Y = variabila explicata prin modelul de regresie;
asa cum s-a anticipat deja, coeficientul de regresie liniara reprezinta, din punct de vedere grafic, tangenta unghiului "φ" pe care linia de regresie reprezentata in sistemul de axe 0X si 0Y il formeaza cu abscisa (0X):
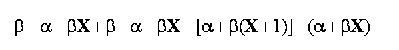
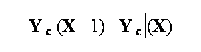
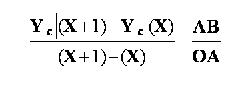

unde:
∆ AOB reprezinta triunghiul dreptunghic format la cresterea cu o unitate a variabilei explicative X - a se vedea figura .
intrucat numitorul fractiei care defineste coeficientul de regresie liniara este intotdeauna pozitiv (fiind egal cu o varianta statistica), coeficientul de regresie liniara are semnul covariantei celor doua variabile ale modelului de regresie liniara (X si Y). In consecinta, o valoare pozitiva a coeficientului de regresie liniara indica o legatura statistica directa intre cele doua variabile, iar o valoare negativa a acestuia indica o legatura statistica inversa intre acestea. Totodata, daca valoarea coeficientului de regresie liniara este 0, inseamna ca intre cele doua variabile nu exista legatura statistica liniara;
coeficientul de regresie liniara este invariant la schimbarea originii:
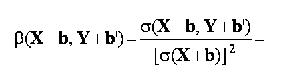
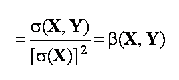
multiplicarea variabilei explicative cu o constanta determina divizarea cu aceeasi constanta a coeficientului de regresie liniara:
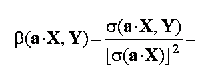
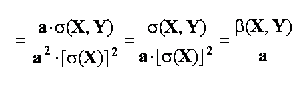
multiplicarea variabilei explicate cu o constanta determina multiplicarea cu aceeasi constanta a coeficientului de regresie liniara:
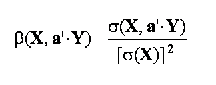
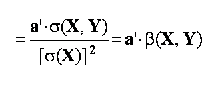
combinand cele doua proprietati anterioare, rezulta:
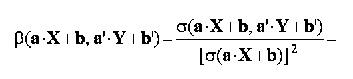
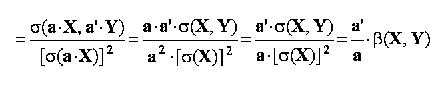
coeficientul de regresie liniara al variabilei Y explicate de variabila X este egal cu inversul coeficientului de regresie liniara al variabilei X explicate de variabila Y. Aceasta proprietate se poate demonstra usor pornind de la raportul dintre cei doi coeficienti:
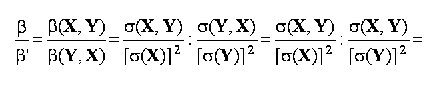
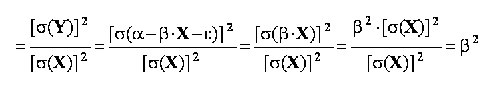
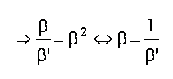
Copyright © 2025 - Toate drepturile rezervate
| Statistica | |||
|
|||
|
| |||
|
| |||
|
|
|||