Preliminarii

1.  Algoritmi

Toti algoritmii descrisi in cadrul acestei lucrari folosesc structuri de date de tip graf. Unele descrieri sint insotite de o analiza a complexitatii algoritmului respectiv. Pentru ca analiza sa poata fi urmarita mai usor de cititor, in cadrul acestei sectiuni sint prezentate notiuni de baza.

Definitia Un algoritm este un set de instructiuni care trebuie executate pentru a se obtine un raspuns la o problema data.

Un algoritm are urmatoarele proprietati (Knuth) (Burdescu, p 10):

- finitudine: trebuie sa se termine intotdeauna dupa un numar finit de pasi (instructiuni);

- determinism: fiecare pas trebuie sa fie exact precizat, in mod riguros si neambiguu;

- generalitate: trebuie sa rezolve problema pentru orice date de intrare din domeniul precizat;

- efectivitate: fiecare instructiune trebuie sa fie exacta si de durata finita.

Ultima proprietate trebuie nuantata, avind in vedere faptul ca memoria oricarui calculator este limitata. Nu intotdeauna operatiile aritmetice se efectueaza exact, in unele cazuri obtinindu-se o aproximare a rezultatelor, cum sint de exemplu implementarile bazate pe aritmetica in virgula mobila (Goldberg).

In cadrul acestei lucrari algoritmii sint descrisi intr-un limbaj de tip Algol, un precursor al limbajului Pascal (cf Aho et al).

Avind un algoritm care rezolva o problema data, urmeaza sa determinam resursele acestuia. Concret, de cita memorie si timp avem nevoie ca sa obtinem solutia problemei? In acest scop facem urmatoarele simplificari: fiecare operatie elementara a algoritmului se executa intr-o unitate de timp, informatiile despre un obiect elementar se memoreaza intr-o locatie de memorie (Livovschi, Georgescu).

Fie f   N   N o functie care indica relatia dintre numarul de valori (date de intrare) prelucrate de un algoritm, si numarul de operatii elementare efectuate de acesta pentru obtinerea rezultatelor. Functia f poate avea o expresie analitica destul de complicata, de aceea consideram inca o functie g   N   N cu o expresie analitica simplificata.

Definitia 2. Functia f are ordinul de marime cel mult g(n), notatie: f I O(g(n)), daca si numai daca exista doua valori, c > 0 si n₀ I N astfel incit pentru orice n > n₀ sa avem f(n) c g(n).

O(g)

Definitia 3. Functia f are ordinul de marime cel putin g(n), notatie: f I W(g(n)), daca si numai daca exista doua valori, c > 0 sin₀ I N astfel incit pentru orice n > n₀ sa avem f(n) c g(n).

W(g)

Definitia 4. Functia f are ordinul de marime g(n), notatie: f I q(g(n)), daca si numai daca exista trei valori, c₁, c₂ > 0 si n₀ I N astfel incit pentru orice n > n₀ sa avem c₁ g(n) f(n) c₂ g(n).

q(g)

Prezentam doua rezultate remarcabile care vor fi folosite pe parcursul lucrarii (Knuth):

(1) Se da un sir de n valori dintr-un domeniu pe care este definita o relatie de ordine totala. Cel mai eficient algoritm de ordonare a sirului dat, care se bazeaza pe comparatii, are complexitate de ordin W(n log n).

(2) Se da un sir de n valori ordonate. Cautarea unei valori (localizarea pozitiei acesteia sau obtinerea unui raspuns negativ) in sirul dat necesita un timp de ordin O(log n).

O categorie speciala de probleme, numite NP-complete, se caracterizeaza prin urmatoarele:

- nu se cunosc algoritmi eficienti (de complexitate polinomiala), se cunosc in schimb algoritmi de complexitate exponentiala pentru rezolvarea acestora;

- o problema NP-completa este polinomial transformabila intr-o alta problema tot NP-completa: daca se rezolva o problema A, solutia unei alte probleme B se poate obtine printr-o transformare in timp polinomial din solutia problemei A.

Cea mai generala problema NP-completa este problema satisfiabilitatii: fiind data o expresie logica in forma normala conjunctiva cu n variabile, sa se determine daca pot fi atribuite valori logice variabilelor astfel incit expresia sa fie adevarata (Cook).

Complexitatea medie. Consideram un algoritm care proceseaza n valori date la intrare. Pentru o anumita configuratie a valorilor, probabilitatea configuratiei fiind p_i, sint necesare f_i(n) operatii. Complexitatea medie a algoritmului este o suma ponderata: .

Exemplu. Algoritmul Quick-sort necesita un timp de ordin O(n log n) in majoritatea cazurilor pentru a ordona un sir de n valori. Exista insa citeva configuratii (foarte putine) care au nevoie de un timp de ordin O(n²) pentru a fi procesate. Complexitatea medie a acestui algoritm este de ordin O(n log n) (Knuth).

Intr-un mod similar se poate defini notiunea de complexitate pentru necesarul de memorie. Aceasta arata cita memorie este necesara pentru rezultatele intermediare si cele de iesire.

Definitiile date mai sus asigura o estimare a eficientei unui algoritm independenta de o implementare practica a acestuia, implementare bazata pe un limbaj concret de programare, urmarindu-se "ascunderea" factorului multiplicativ. Totusi acest factor nu poate fi intotdeauna ignorat, deoarece exista probleme care admit mai multi algoritmi cu acelasi ordin de complexitate. In asemenea situatii se poate determina, pe baza unor experimente, care este algoritmul cel mai eficient din punct de vedere practic. Pot fiu luate in considerare mai multe criterii: timpul mediu de raspuns cel mai bun, simplitatea implementarii etc.

Se apreciaza ca un algoritm este eficient daca are complexitate de ordin cel mult O(n log n). Daca volumul datelor de intrare este mic (pina la ordinul miilor) se poate accepta si un algoritm de ordin O(n²).

2. Grafuri: notiuni de baza

Grafuri orientate

Definitia 5. Un graf orientat este un cuplu G   (X, U ), unde X este o multime finita si nevida de elemente numite virfuri, si U   X X este o multime de elemente numite arce.

In continuare vom nota |X |   n, |U |   m; aceste notatii vor fi folosite pe parcursul intregii lucrari, si au fost preluate din literatura franceza (Berge) (Gondran, Minoux). Notatiile consacrate in literatura anglo-saxona sint: V (vertices) si E (edges).

Fie un arc u = (x,y) I U. Spunem ca arcul u are sensul (sau orientarea) de la x la y. Virful x este extremitate initiala si predecesorul lui y, si virful y este extremitate finala si succesorul lui x. Deci in precizarea unui arc conteaza ordinea virfurilor.

Fie un arc u = (x,y) I U. Daca exista si arcul u' = (y,x) I U atunci fiecare arc este inversul celuilalt.

Doua virfuri sint adiacente daca intre ele exista un arc. Doua arce distincte sint adiacente daca au o extremitate comuna.

Definitia 6. Un graf orientat este un cuplu G   (X, G ), unde X este o multime de elemente numite virfuri, si G este o aplicatie multivoca G : X   X (adica o functie definita pe X cu valori in familia P(X) a partilor lui X).

G (x) desemneaza lista succesorilor virfului x. Daca x I X atunci y I G (x) precizeaza ca de la virful x la virful y exista un arc si spunem ca y este succesor al lui x. Spunem ca x este predecesor al lui y si notam x I G  ¹(y). G  ¹(x) desemneaza lista predecesorilor virfului x.

Fiind dat un graf G   (X, G ), graful G'   (X, G  ¹) este graful invers asociat grafului G. In literatura de specialitate acesta este numit graful transpus, deoarece matricea de adiacenta a acestui graf este transpusa matricei grafului original.

Definitia 7. Fie un graf G   (X, G ) si x I X un virf. Notam cu g⁺(x) numarul succesorilor sai, adica |G (x)|; acest numar se numeste semigradul exterior al lui x. Notam cu g (x) numarul predecesorilor sai, adica |G  ¹(x)|; acest numar se numeste semigradul interior al lui x. Suma g(x)   g⁺(x) + g (x) se numeste gradul lui x. Daca g(x)   0 spunem ca virful x este izolat.

Cele doua definitii sint analoge:

G (x)    ; (x,y) I U daca si numai daca y I G(x).

Grafuri particulare. Un graf orientat este simetric daca pentru orice pereche de virfuri x, y I X avem: (x,y) I U implica (y,x) I U.

Un graf este bipartit daca exista o partitie X   X₁X₂ astfel incit pentru orice (x,y) I U avem x I X₁ si y I X₂.

Un graf G'   (A, V ) este subgraf al grafului G = (X, U ) daca A   X si V   (A A)U.

Un graf G'   (X, V ) este graf partial al grafului G   (X, U ) daca V   U.

Un graf G'   (A, V ) este subgraf partial al grafului G   (X, U ) daca A   X si V   (A A)U.

Sa observam ca un graf partial are aceeasi multime de virfuri cu graful initial, si doar o parte din arcele acestuia. In schimb un subgraf are doar o parte din virfurile grafului initial, si toate arcele acestuia care au ambele extremitati in aceasta submultime de virfuri.

Definitia 8 (drumuri intr-un graf). Fiind dat un graf orientat G   (X, U ), un drum in graful G este o succesiune de arce cu proprietatea ca extremitatea terminala a unui arc coincide cu extremitatea initiala a arcului urmator din drum. Un drum se poate defini si prin succesiunea de virfuri care sint extremitati ale arcelor ce compun drumul: o succesiune de virfuri cu proprietatea ca orice doua virfuri consecutive sint unite printr-un arc.

Un drum intr-un graf este:

- simplu, daca nu foloseste de doua ori un acelasi arc;

- compus, daca nu e simplu;

- elementar, daca nu trece de doua ori prin acelasi virf;

- eulerian, daca este simplu si foloseste toate arcele grafului;

 hamiltonian, daca este elementar si trece prin toate virfurile grafului;

- circuit, daca extremitatea initiala a drumului coincide cu cea finala.

Un lant este o succesiune de arce cu proprietatea ca orice arc are un virf comun cu arcul precedent si celalalt virf comun cu arcul urmator.

Sa observam ca intr-un drum toate arcele au aceeasi orientare, de la virful initial la virful final. In schimb intr-un lant fiecare arc poate avea orice orientare.

Grafuri neorientate

Definitia 9. Un graf neorientat este un cuplu G = (X, U ), unde X este o multime de elemente numite virfuri, si U este o multime de perechi neordonate de virfuri numite muchii. O muchie (x,y) nu are orientare, astfel ca (x,y)   (y,x).

O muchie este incidenta virfurilor care sint extremitati ale sale. Doua virfuri sint adiacente daca intre ele exista o muchie. Doua muchii sint adiacente daca au o extremitate comuna. Gradul unui virf x este numarul de muchii incidente cu acesta si se noteaza g(x).

Definitia 10. Un lant este o succesiune de muchii cu proprietatea ca orice muchie are un virf comun cu muchia precedenta si celalalt virf comun cu muchia succesoare.

In mod analog definim notiunea de ciclu corespunzatoare notiunii de circuit de la grafuri orientate.

Grafuri ponderate

Definitia 1 Un graf ponderat este un triplet G   (X, U, c), unde X si U au semnificatiile cunoscute, si c : U   R₊ este o functie cost care asociaza fiecarui arc (fiecarei muchii) o valoare (pondere).

Un graf ponderat poate fi definit si cu ajutorul functiei G

Exemplu. Avem o harta rutiera care contine urmatoarele informatii: pozitia fiecarei localitati, legaturile directe dintre localitati impreuna cu distanta si timpul necesare parcurgerii fiecarei legaturi. Trebuie sa determinam un drum de cost minim (criteriul fiind distanta sau timpul) dintre doua localitati. Graful asociat problemei se obtine luind ca virfuri localitatile, si inlocuind fiecare legatura cu doua arce avind acelasi cost si orientari opuse daca legatura este in ambele sensuri, sau cu un singur arc daca legatura este intr-un singur sens.

3. Tehnici de reprezentare

Reprezentare grafica

Sa consideram citeva puncte de interes ale unei localitati si legaturile directe dintre acestea. Punctele de interes sint reprezentate prin virfuri ale grafului, si legaturile dintre acestea prin arce. Daca toate legaturile dintre doua puncte sint in ambele sensuri, atunci graful este neorientat; in acest caz o muchie este reprezentata printr-o linie dreapta. Daca exista cel putin o legatura intr-un singur sens, atunci graful este orientat; in acest caz este precizata orientarea arcului.

 

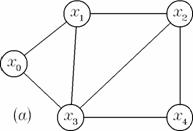
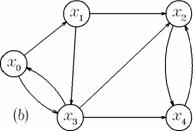
Figura  Un graf neorientat (a), un graf orientat (b).

Pentru graful orientat din figura 1 (b) avem:

X   

U   

Functia G este definita astfel:

G (0)    ; G (1)    ; G (2)   

G (3)    ; G (4)   

Exemple de trasee pentru graful neorientat din figura 1 (a):

(x₀, x₁, x₂, x₄, x₃, x₀) - ciclu hamiltonian;

(x₁, x₀, x₃, x₁, x₂, x₃, x₄, x₂) - lant eulerian.

Exemple de trasee pentru graful orientat din figura 1 (b):

(x₀, x₁, x₃, x₂, x₄) - drum hamiltonian;

(x₀, x₁, x₂, x₃, x₄) - lant; nu este drum deoarece nu exista

arcul (x₂, x₃) ci numai arcul (x₃, x₂).

Reprezentare bazata pe lista arcelor

Se folosesc doua masive, ambele au un numar de elemente egal cu numarul de arce, si pentru fiecare arc se memoreaza cele doua extremitati. Exemplu:

Extr_ini 0 0 1 1 2 3 3 3 4

Extr_fin 1 3 2 3 4 0 2 4 2

Pentru un graf ponderat se foloseste un al treilea masiv de memorie, unde se memoreaza costurile arcelor.

Reprezentare bazata pe functia G  (liste de succesori)

Se folosesc doua masive de memorie; primul masiv are n 1 elemente, si indica pozitiile din cel de-al doilea masiv unde se gasesc valorile functiei G pentru fiecare virf al grafului; al doilea masiv are m elemente.

Graful orientat din figura 1 (b) se reprezinta astfel (consideram ca indicii celor doua masive iau valori incepind cu 0):

(H) Pozitii G 0 2 4 5 8 9

(S) Valorile 1 3 2 3 4 0 2 4 2

functiei G (0) (1) (2) (3) (4) (5) (6) (7) (8)

Primul masiv (H) are semnificatia de tabela hash pentru o cautare rapida in cel de-al doilea masiv (S). Fiecare lista de succesori G (x) se descrie pe pozitiile de la H [x] pina la H [x 1]- Pentru a usura citirea corespondentei dintre cele doua masive am pus in evidenta indicii pentru masivul care reprezinta valorile functiei G

Pentru un graf ponderat se foloseste un al treilea masiv de memorie, unde se memoreaza costurile arcelor.

Tehnica descrisa mai sus este cea mai compacta si mai eficienta pentru majoritatea algoritmilor care se bazeaza pe parcurgerea unui graf (Gondran, Minoux, p 8-9). In acelasi timp aceasta poate fi folosita numai pentru grafuri statice si numai daca se cunoaste de la inceput topologia acestuia. Pentru grafuri care se actualizeaza in mod dinamic se recomanda alte structuri de date adecvate acestui scop (de exemplu liste inlantuite).

In ultima sectiune a acestui capitol este descris un algoritm care permite obtinerea reprezentarii unui graf pe baza functiei G .

Reprezentare implicita

Spre deosebire de reprezentarile descrise mai sus, care sint explicite, in continuare vom vedea ca legaturile dintre virfuri pot fi deduse dintr-o harta descrisa intr-un anumit mod.

Fie un labirint de forma dreptunghiulara, cu o harta cunoscuta avind n linii si m coloane. In continuare prezentam doua posibile reprezentari ale acestuia.

(1) Consideram mai intii un labirint in care peretii sint construiti din blocuri avind forma unui patrat de latura unitate. Descrierea este foarte simpla, fiecare element a_ij avind semnificatia:

a_ij

Liniile sint numerotate de la 0 la n-1 de sus in jos, si coloanele sint numerotate de la 0 la m-1 de la stinga la dreapta.

Directiile posibile de deplasare dintr-o camera de coordonate (x,y) sint:

(x,y 1) spre nord;       (x 1,y) spre vest;

(x,y 1) spre sud;         (x 1,y) spre est.

Aceasta reprezentare permite doar descrierea unui graf neorientat.

2) In al doilea caz labirintul este alcatuit din camere, fiecare camera putind comunica sau nu cu oricare din camerele vecine. Descrierea este mai complexa, fiecare camera avind asociata o valoare a_ij care se reprezinta pe 4 biti astfel:

- bitul 0 are valoarea zero daca exista usa spre est;

- bitul 1 are valoarea zero daca exista usa spre nord;

- bitul 2 are valoarea zero daca exista usa spre vest;

- bitul 3 are valoarea zero daca exista usa spre sud.

Liniile sint numerotate de la 0 la n-1 de sus in jos, si coloanele sint numerotate de la 0 la m-1 de la stinga la dreapta.

O camera de iesire se afla pe frontiera labirintului si are o usa care permite iesirea in directia respectiva.

Exemple

(0,y,?0??), (x,0,??0?), (m-1,y,???0), (x,n-1,0???).

Am marcat cu ? bitii a caror valoare nu intereseaza.

Spre deosebire de reprezentarea anterioara, aceasta permite descrierea unui graf orientat, astfel ca poate fi modelat cazul in care o usa se deschide intr-un singur sens.

Reprezentarile implicite sint foarte folosite in prelucrarea imaginilor reprezentate in format bitmap.

Conventii pentru reprezentare

Majoritatea algoritmilor descrisi in cadrul acestei lucrari folosesc reprezentarea bazata pe functia G . Un graf neorientat va fi reprezentat ca un graf orientat simetric. Intr-o implementare concreta, reprezentarea bazata pe lista arcelor este necesara doar in faza de creare a grafului.

Reprezentarea bazata pe lista arcelor este folosita de algoritmul lui Kruskal, care are nevoie de lista arcelor, nu are importanta orientarea acestora. Algoritmii de tip Bellman pot folosi oricare din cele doua tehnici de reprezentare.

Pentru o aplicatie eficienta bazata pe grafuri recomandam urmatoarea strategie. Intr-o faza anterioara lansarii aplicatiei graful se construieste pe baza listei arcelor, dupa care se memoreaza in fisier reprezentarea bazata pe functia G . Toate informatiile se memoreaza in format binar astfel: mai intii valorile n si m, lista H (n 1 valori), lista G  (m valori), si daca este nevoie lista C.

4. Parcurgerea unui graf

Sa presupunem ca este dat un graf G, orientat sau neorientat, si fie doua virfuri x si y in G; cum putem determina daca exista un drum intre x si y? In mod intuitiv, am dori sa plecam din x, sa examinam toate virfurile care pot fi atinse din x traversind arcuri din G, si sa ne oprim atunci cind depistam virful y sau cind examinam toate virfurile care ar putea fi atinse plecind din x. Mai general, dorim sa efectuam o operatie oarecare pentru fiecare virf - sa o numim Visit. Acest proces se numeste parcurgere (vizitare) a grafului G plecind din x (Larry, Denenberg, p 432).

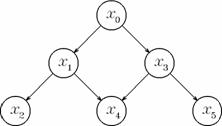
Figura 2. Doua tehnici de parcurgere plecind din virful x₀:

in latime (breadth first search): x₀ - x₁ - x₃ - x₂ - x₄ - x₅

in adincime (depth first search): x₀ - x₁ - x₂ - x₄ - x₃ - x₅

Trebuie sa remarcam faptul ca o parcurgere incepind cu virful x viziteaza exact acele virfuri y cu proprietatea ca exista un drum in G de la x la y. Tehnicile de parcurgere sint cel mai adesea folosite tocmai pentru a vizita virfurile intr-o anumita ordine data de legaturile dintre acestea.

Figura 2 prezinta un exemplu de parcurgere a unui graf in latime si in adincime. Aceste tehnici vor fi detaliate in capitolele urmatoare, unde vor fi prezentate si aplicatii.

Pe parcursul lucrarii vom intilni foarte frecvent secvente asemanatoare celei de mai jos:

for (each x I X) do

for (each y I G (x)) do

Prelucrare-arc (x,y);

Aceasta secventa parcurge lista arcelor unui graf reprezentat pe baza functiei G (liste de succesori). Sa analizam complexitatea acestei secvente, presupunind ca:

- graful este reprezentat pe baza functiei G ;

- prelucrarea unui arc dureaza o unitate de timp - O(1).

Pentru un anumit virf x, in ciclul for interior se prelucreaza atitea arce citi succesori are virful x, adica |G (x)|. Consideram inca o unitate de timp pentru trecerea de la un virf x la urmatorul, la o iteratie a ciclului for exterior. Daca x I obtinem:

1 G (0)| 1 G (1)| 1 G (n-1)| n m

Aceasta secventa are complexitate de ordin O(n m

Nu am contorizat separat actiunea de trecere la urmatorul virf din lista de succesori a virfului x, deoarece am considerat ca aceasta este inclusa in lista de operatii elementare care efectueaza prelucrarea arcului (x,y).

Am ignorat faptul ca prelucrarea unui arc (ciclul for interior) presupune in mod evident mai multe operatii elementare (aritmetice si logice pe care le efectueaza procesorul), decit simpla actiune de trecere la urmatorul virf din multimea X (ciclul for exterior). Conform definitiei complexitatii unui algoritm, constanta multiplicativa nu este relevanta. Desigur, aceasta simplificare este destul de grosiera, dar ea se face din punct de vedere teoretic pentru a evalua marginea superioara a complexitatii unui algoritm studiat.

5. Obtinerea listelor de succesori

Descriem in continuare un algoritm de conversie a listei de arce in liste de succesori (functia G ). Acest algoritm poate fi folosit si pentru a construi reprezentarea G^-1 a grafului invers asociat unui graf dat.

Algoritm Conversie-Arce-Gamma;

Intrare. Lista U a arcelor unui graf: (x_i, y_i), i 0, 1, , m-

Iesire. Listele de succesori, memorate in doua masive, H si S.

begin

Ordoneaza lista U a arcelor unui graf: (x_i, y_i), i 0, 1, , m-1;

Prin parcurgerea listei U se determina n, numarul de virfuri;

for (k 0, , n) do H[k] 0;

k 0; i 0;

while (k < m) do begin

a x[k];

repeat

i i 1;

until (i m) or (x[i] > a);

H[a 1] i; k i;

end

for (k 1, , n) do

if (H[k] 0) then

H[k] H[k-1];

for (i = 0, 1, , m-1) do S[i] y[i];

end (algoritm).

Ideea algoritmului este urmatoarea. Dupa ordonarea arcelor se parcurge aceasta lista (while) cu scopul de a stabili repere pentru pozitiile pe care se vor memora succesorii fiecarui virf. Concret, pentru fiecare virf a se completeaza H[a 1], care reprezinta de fapt prima pozitie ocupata de un succesor al lui a

Este posibil ca unele virfuri sa nu aiba succesori, si de aceea parcurgerea masivului H completeaza reperele si pentru aceste virfuri. In final se completeaza masivul S cu listele de succesori, concret cu virfurile finale ale arcelor.

Ordonarea arcelor se efectueaza intr-un timp de ordin O(m log m). Lista de arce este parcursa intr-un timp de ordin O(m)   O(m log m). Lista H se initializeaza si se corecteaza intr-un timp de ordin O(n). Rezulta

Teorema Conversia listei arcelor in liste de succesori (functia G ) necesita un timp de ordin O(m log m n).

Lista de succesori a unui virf x poate fi parcursa astfel:

for (j  H x H x 1, , H x 1]-1) do begin

y S[j]; Prelucrare-arc (x,y);

end

Algoritmul de conversie poate fi folosit pentru a genera inversul unui graf dat. Se genereaza lista arcelor grafului invers - (y,x) pentru (x,y), si in final aceasta lista este convertita in functia G ^-

6. Grafuri dinamice

Exista unele probleme care cer ca pe parcurs sa se elimine din graf unele arce prelucrate, fara sa fie nevoie sa se introduca ulterior alte arce noi. Pentru aceste probleme se poate adopta urmatoarea tehnica de reprezentare, descrisa in continuare. Se introduce un masiv suplimentar F, care pastreaza initial limitele de sus ale pozitiilor succesorilor fiecarui virf. Masivul F se completeaza astfel:

for (x 0, 1, , n-1) do F[x] H[x 1];

Ulterior, daca se doreste eliminarea unui arc cu originea in x, al carui succesor este memorat pe pozitia j (avem H[x]   j < F[x]), se copiaza pe aceasta pozitie succesorul aflat pe ultima pozitie (F[x]-1) din lista asociata lui x. Daca graful este ponderat, aceeasi operatie se repeta pentru costul arcului eliminat.

Un succesor al virfului x, aflat pe pozitia j, se elimina astfel:

F[x] F[x] - 1; S[j] S[F[x]];

Se poate adopta si o alta solutie, mai simpla dar cu eficienta ceva mai mica, bazata doar pe masivele H si S. Eliminarea unui succesor de pe pozitia j (H[x]   j < H[x]) se face mult mai simplu, inlocuind valoarea de pe pozitia respectiva cu o valoare negativa:

S[j] -1;

Dar aceasta presupune ca, de fiecare data cind se parcurge lista de succesori, fiecare valoare S[j] trebuie verificata, si daca nu este negativa ea reprezinta un succesor valid.