Semnaturi cu Cheie Publica

Semnaturi cu Cheie Publica

O problema structurala in folosirea criptografiei cu cheie secreta pentru semnaturi digitale este aceea ca oricine trebuie sa se increada in Big Brother. Mai mult decat atat, Big Brother poate citi toate mesajele semnate. Cei mai logici candidati pentru a juca rolul lui Big Brother sunt guvernul, bancile, oamenii legii. Aceste organizatii nu inspira insa incredere totala tuturor cetatenilor. De aceea ar fi frumos daca semnarea documentelor nu ar necesita existenta unei astfel de autoritati de incredere.

Din fericire, criptografia cu cheie publica isi poate aduce aici o importanta contributie. Sa presupunem ca algoritmii de criptare si decriptare cu cheie publica au proprietatea ca E(D(P))=P in plus fata de proprietatea uzuala D(E(P)) =P. (RSA are aceasta proprietate deci presupunerea nu este nerezonabila). Sa presupunem ca Alice poate trimite un text clar semnat, P, lui Bob transmitand E_B(D_A(P)). O observatie importanta aici este aceea ca Alice cunoaste atat propria sa cheie seereta cat si cheia publica a lui Bob, E_B, astfel incat constructia acestui mesaj este pentru Alice un lucru realizabil.

Cand Bob primeste mesajul, el il transforma, folosindu-si cheia privata, ca de obicei, rezultand D_A(P), dupa cum este aratat si in Fig. 2-10. El memoreaza acest text intr-un loc sigur si apoi decripteaza, folosind E_A, pentru a obtine textul clar original.

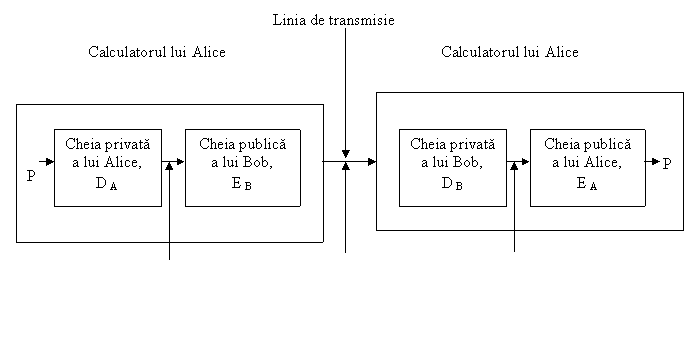
D_A(P) E_B(D_A(P)) D_A(P)

Fig. 2-10. Semnaturi digitale folosind criptografia cu cheie publica.

Pentru a vedea cum lucreaza semnatura, sa presupunem ca Alice neaga ulterior trimiterea mesajului P lui Bob. Atunci cand cazul ajunge in fata curtii, Bob poate aduce ca probe atat P cat si D_A(P). Judecatorul poate verifica usor ca Bob are un mesaj valid criptat cu D_A, doar aplicand E_A asupra lui. Deoarece Bob nu stie care este cheia privata a lui Alice, singurul mod prin care Bob poate sa fi primit mesajul criptat cu aceasta cheie privata este ca Alice in persoana sa-l fi trimis trimis. Cat timp va fi inchisa pentru minciuna si frauda, Alice va avea suficient timp sa conceapa noi algoritmi cu cheie publica interesanti.

Cu toate ca folosirea criptografiei cu cheie publica pentru semnaturi digitale este o schema eleganta, exista probleme legate mai degraba de mediul in care acestea opereaza decat de algoritmul de la baza. De exemplu, Bob poate proba ca mesajul a fost trimis de catre Alice atata vreme cat D_A ramane secret. Daca Alice dezvaluie cheia sa secreta, acest argument nu va mai fi valabil, deoarece oricine poate sa fi trimis mesajul, chiar si Bob.

Problema poate aparea, de exemplu, daca Bob este agentul de vanzari al lui Alice. Alice ii spune lui Bob sa cumpere niste actiuni si sa le pastreze. Imediat dupa aceea, pretul scade vertiginos. Pentru a repudia mesajul sau catre Bob, Alice face o plangere la politie, pretinzand ca i-a fost sparta casa si furata cheia secreta. In functie de legislatia din tara sau tinutul sau, ea poate fi sau nu raspunzatoare legal, in special daca pretinde ca a descoperit spargerea cand s­-a intors acasa de la munca, la cateva ore mai tarziu.

O alta problema cu schema de semnatura este ce se intampla daca Alice decide sa-si schimbe cheia. A face acest lucru este evident legal si este probabil o idee buna sa o faca periodic. Daca in justitie apare mai tarziu un caz, asa cum s-a povestit mai sus, judecatorul va aplica actualul E_A la D_A(P) si va descoperi ca nu se obtine P. Bob va fi atunci intr-o situatie delicata. In consecinta, apare necesitatea ca o autoritate sa inregistreze toate schimbarile de chei si datele acestora.

In principiu, orice algoritm cu cheie publica poate fi folosit pentru semnaturi digitale. Standardul de factor in industrie este algoritmul RSA. Multe produse pentru securitate il folosesc. Totusi in 1991, NIST (National Institute of Standards and Technology) a propus o varianta a algoritmului cu cheie publica El Gamal pentru noul lor standard DSS (Digital Signature Standard - Standard pentru Semnatura Digitala). El Gamal isi bazeaza securitatea pe dificultatea calculului logaritmilor discreti si nu pe dificultatea factorizarii numerelor mari.

Ca de obicei, cand guvernul incearca sa impuna standarde criptografice, s-a iscat o reactie lagonista de masa. DSS a fost criticat pentru a fi:

1. Prea secret (NSA a proiectat protocolul pentru folosirea El Gamal).

2. Prea nou (El Gamal nu a fost inca suficient analizat).

3. Prea lent (de 10 pana la 40 de ori mai lent decat RSA in verificarea semnaturilor).

4. Prea nesigur (chei fixe de 512 biti).

Dupa o revizuire ulterioara, cel de-al patrulea motiv a fost eliminat fiindca s-au permis chei de pana la 1024 biti. Nu este inca clar daca DSS va prinde sau nu. Pentru mai multe detalii, a se vedea (Kaufman s.a., 1995; Schneier,1996; si Stinson, 1995).