 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
CALCULUL SIMBOLIC IN MATLAB
In MATLAB pot fi efectuate in mod simbolic o serie de calcule matematice cum ar fi calculul unor derivate, integrale, limite sau serii Taylor; in cadrul algebrei liniare determinarea inversei, valorilor proprii, determinantului sau descompunerii unei matrici simbolice, metode de simplificare a expresiilor algebrice, rezolvarea simbolica si numerica a ecuatiilor algebrice si diferentiale, functii speciale s.a.
Toolbox-ul Symbolic Math defineste un nou tip de date MATLAB numite obiecte simbolice. Un obiect simbolic este o structura de date de tip sir de caractere ce reprezinta simbolul utilizat pentru a reprezenta o variabila, o expresie matematica sau o matrice.
Crearea de variabile si expresii simbolice
Pentru construirea de variabile si expresii simbolice se utilizeaza comanda sym. De exemplu, comenzile:
a = sym('alpha')
xb= sym('beta')
creeaza o variabila simbolica a care este tiparita pe ecran alfa si o variabila simbolica b ce este tiparita beta. Daca se da comanda a+b, raspunsul va fi:
ans =
alfa+beta
In acelasi mod se procedeaza in cazul expresiilor
matematice. De exemplu, daca dorim sa reprezentam simbolic o expresie in care
apare raportul: ![]() , atunci utilizam comanda:
, atunci utilizam comanda:
r=sym('(1+sqrt(5))/2')
Acum pot fi efectuate diferite calcule matematice utilizand variabila r. Spre exemplu, relatia:
f=r^2-r-1
returneaza raspunsul:
f = (1/2+1/2*5^(1/2))^2-3/2-1/2*5^(1/2)
Daca se da comanda: simplify(f) se obtine valoarea 0.
Sa presupunem ca dorim sa studiem functia patatica: f=ax2+bx+c. Comanda
f = sym('a*x^2+b*x+c')
asigneaza expresia simboica ax2 + bx + c variabilei f. In acest caz insa nu se creeaza variabile corespunzatoare termenilor a, b, c si x. Pentru a putea efectua opeatii matematice cu aceasta expresie trebuie create variabilele in mod explicit, adica:
a = sym('a')
b = sym('b')
c = sym('c')
x = sym('x')
sau mai simplu:
syms a b c x (care este mai recomandata deoarece este mai putin de scris).
Conversiile numerice
Consideram urmatoarea marime constanta:
t = 0.1
Functia sym are patru optiuni pentru o reprezentare simbolica a valorii numerice aflate in t. Acestea sunt urmatoarele:
- optiunea 'f' : sym(t,'f')
returneaza o reprezentare simbolica in virgula mobila:
'1.999999999999a'*2^(-4)
- optiunea 'r' : sym(t,'r')
returneaza forma rationala a numarului 1/10 (aceasta este setarea implicita a functiei sym)
- optiunea 'e' sym(t,'e')
returneaza forma rationala a lui t plus diferenta intre valoarea rationala teoretica a lui t si valoarea actuala in virgula mobila
sym(t,'e')
ans = 1/10+eps/40
- optiunea 'd' returneaza numarul t pe atatea cifre zecimale cate specifica instructiunea digits (valoarea implicita fiind de 32 de cifre). sym(t,'d')
ans = .10000000000000000555111512312578
digits(7)
sym(t,'d')
ans = .1000000
O utilizare importanta a functiei sym este conversia unei matrici din forma numerica in forma simbolica. Daca avem urmatoarea matrice:
A = 1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
atunci instructiunea
A = sym(A)
conduce la urmatorul rezultat
A =
[ 1, 1/2, 1/3]
[ 1/2, 1/3, 1/4]
[ 1/3, 1/4, 1/5]
Crearea de functii matematice simbolice
Exista doua modalitati de a crea functii matematice:
folosirea expresiilor simbolice;
crearea de fisiere matlab.
Utilizand expresii simbolice se folosesc comenzile urmatoare:
syms x y z
r = sqrt(x^2 + y^2 + z^2)
t = atan(y/x)
f = sin(x*y)/(x*y)
care genereaza expresiile simbolice r, t, si f.
Crearea unui fisier matlab ce contine o functie simbolica permite o utilizare mai generala a functiilor. Spre exemplu crearea functiei sin(x)/x poate fi realizata astfel:
function z = sinc(x)
if isequal(x,sym(0))
z = 1;
else
z = sin(x)/x;
end
Calcule simbolice
Calculul derivatei Spre exemplu, pentru a calcula derivata simbolica a functiei sinus, cream expresia:
syms a x
f = sin(a*x)
dupa care folosind functia diff se calculeaza derivata acesteia in raport cu x.
diff(f)
ans = cos(a*x)*a
Se poate calcula derivata in raport cu variabila a cu comanda:
diff(f,a)
care returneaza df/da.
ans = cos(a*x)*x
Pentru a calcula derivata de ordinul 2 se utilizeaza urmatoarea comanda:
diff(f,x,2)
care returneaza urmatorul rezultat:
ans = -sin(a*x)*a^2
Calculul integralei Daca f este o expresie simbolica, atunci comanda:
int(f,v)
determina integrala nedefinita a lui f in raport cu v. De asemenea este posibil calculul integralei definite folosind comanda:
int(f,v,a,b),
unde f este expresia ce trebuie integrata, v, variabila dupa care se face integrarea, iar a si b sunt limitele de integrare.
Calculul limitelor
Daca f este o expresie simbolica, atunci comanda:
limit(f,x,a)
sau limit(f,a), calculeaza ![]()
iar limit(f,x,a,'left') si limit(f,x,a,'right') calculeaza limitele la dreapta si la stanga.
Calculul
unor serii Suma unor serii de numere poate fi calculata utilizand
comanda symsum. Spre exemplu, suma
seriei ![]() este
este ![]()
syms x k
s1 = symsum(1/k^2,1,inf)
s1 = 1/6*pi^2
Simplificari Iata trei expresii diferite:
syms x
f = x^3-6*x^2+11*x-6
g= (x-1)*(x-2)*(x-3)
h = x*(x*(x-6)+11)-6
Folosind urmatorele comenzi ele pot fi puse sub forma obisnuita:
pretty(f), pretty(g), pretty(h)
x3 - 6 x2 + 11 x - 6
(x - 1) (x - 2) (x - 3)
x (x (x - 6) + 11) - 6
Aceste expresii sunt trei reprezentari diferite ale aceleiasi functii matematice. Fiecare din cele trei forme poate fi preferata intr-o anumita situatie. Prima forma este cea mai des utilizata reprezentare a unui polinom. Cea de-a doua este forma factorizata, cea care prezinta radacinile polinomului. Cea de-a treia forma este reprezentarea Horner.
Exista cateva functii ce aplica o serie de identitati algebrice si trigonometrice pentru a transforma o reprezentare a unei functii in alta posibil mai simpla sau mai utila. Aceste functii sunt: collect, expand, horner, factor, simplify, si simple.
Functia collect grupeaza termenii polinomului in ordine descescatoare a puterilor variabilei simbolice:
f=(x-1)*(x-2)*(x-3)
collect(f)
x^3-6*x^2+11*x-6
Functia expand asigura distributivitatea inmultirii fata de adunare. Iata cateva exeple:
|
f |
expand(f) |
|
a*(x + y) (x-1)*(x-2)*(x-3) x*(x*(x-6)+11)-6 exp(a+b) cos(x+y) |
a*x+a*y x^3-6*x^2+11*x-6 x^3-6*x^2+11*x-6 exp(a)*exp(b) cos(x)*cos(y)-sin(x)*sin(y) |
Functia horner transforma un polinom in reprezentarea Horner a acestuia.
f= x^3-6*x^2+11*x-6
horner(f)
-6+(11+(-6+x)*x)*x
Functia factor exprima un polinom cu coeficienti rationali in produs de polinoame de grad minim.
f= x^3-6*x^2+11*x-6
factor(f)
(x-1)*(x-2)*(x-3)
Functia simplify poate fi utilizata pentru simplificarea unor expresii ce contin identitati algebrice, puteri intregi sau fractionale, functii trigonometrice, exponentiale sau logaritmice si functii speciale.
f= x*(x*(x-6)+11)-6
simplify(f)
x^3-6*x^2+11*x-6
f=(1-x^2)/(1-x)
simplify(f)
x+1
Rezolvarea ecuatiilor algebrice
Daca S este o expresia simbolica, atunci solve(S) determina valorile variabilei simbolice pentru care S este zero. De exemplu, ecuatia de gradul II se rezolva astfel:
syms a b c x
S = a*x^2 + b*x + c;
solve(S)
ans =
[1/2/a*(-b+(b^2-4*a*c)^(1/2))]
[1/2/a*(-b-(b^2-4*a*c)^(1/2))]
Daca se doreste rezolvarea unei ecuatii de forma f(x) = q(x), trebuie folosite siruri de caractere intre apostroafe:
s = solve('cos(2*x)+sin(x)=1')
s =
[ 0] [ pi] [ 1/6*pi] [ 5/6*pi]
Rezolvarea ecuatiilor diferentiale
Functia dsolve
calculeaza solutii simbolice pentru ecuatii diferentiale ordinare. Ecuatiile
trebuie specificate prin expresii simbolice ce contin litera D pentru a nota
diferentiala. D2, D3, . DN corespund derivatei de ordinul 2, 3 . . . N. In mod
implicit, variabila independenta este t. Astfel, expresia D2y reprezinta relatia ![]() . Conditiile initiale pot fi specificate prin adaugarea de
ecuatii. Daca nu sunt specificate conditiile initiale, solutiile vor contine
constante de integrare C1, C2, etc.
. Conditiile initiale pot fi specificate prin adaugarea de
ecuatii. Daca nu sunt specificate conditiile initiale, solutiile vor contine
constante de integrare C1, C2, etc.
Exemple:
dsolve('Dy=1+y^2')
ans = tan(t+C1)
Pentru a specifica conditiile initiale se utilizeaza expresia:
y = dsolve('Dy=1+y^2','y(0)=1')
y = tan(t+1/4*pi)
Observatie: Variabila y se afla in spatiul de lucru al MATLAB-ului, insa variabila independenta t trebuie declarata cu comanda syms t , altfel comanda diff(y,t) va da eroare.
Ecuatiile neliniare pot avea mai multe solutii, chiar daca se dau conditiile initiale.
x = dsolve('(Dx)^2+x^2=1','x(0)=0')
x = [-sin(t)]
[ sin(t)]
y = dsolve('D2y=cos(2*x)-y','y(0)=1','Dy(0)=0','x')
simplify(y)
y = -2/3*cos(x)^2+1/3+4/3*cos(x)
Calculul transformatei Z directe si inverse
Transformata Z directa pentru un sir de numere ![]() este data de relatia:
este data de relatia: ![]()
In MATLAB exista doua posibilitati pentru calculul transformatei Z:
F =ztrans(f) sau F(z) = symsum(f(n)/z^n, n, 0, inf),
unde n este variabila simbolica a expresiei f.
f = sin(a*n)
ztrans(f,w)
ans= sin(a)*w/(1-w*cos(a)+w^2)
Transformata Z inversa are urmatoarea sintaxa:
f = iztrans(F)
Expresia F are z ca variabila independenta implicita.
Calculul transformatei Laplace directe si inverse
Transformata Laplace pentru o functie f(t) este data
de relatia: 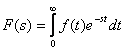
In Matlab se utilizeaza comanda L = laplace(F) unde expresia simbolica F are pe t ca variabila independenta implicita. Functia returnata este o functie in s.
f = t^4
laplace(f)
ans= 24/s^5
Transformata
Laplace inversa este data de relatia 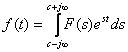 , iar in MATLAB se utilizeaza comanda: F =
ilaplace(L) cu variabila independenta implicita s.
, iar in MATLAB se utilizeaza comanda: F =
ilaplace(L) cu variabila independenta implicita s.
f = 1/s^2
ilaplace(f)
ans= t
TEMA:
Sa se calculeze derivatele de ordinul I si II pentru urmatoarele functii:
![]() ,
, 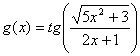 ,
, ![]()
Sa se calculeze urmatoarele integrale:
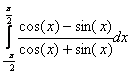 ,
, ![]() ,
, ,
,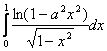 ,
, 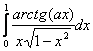
Sa se calculeze urmatoarele limite si serii:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Sa se rezolve urmatoarele ecuatii diferentiale:
y"+(y2-1)y'+y=0, y"+5y'y2+y=0
y"'+7y"-y'tg(y')+3y+1=0, in C.I. y"'(0)=0.4, y"(0)=0,y'(0)=0.2
Sa se rezolve urmatoarele sisteme de ecuatii:
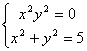 ,
, ![]()
Sa se calculeze transformata Z directa pentru sirurile:
f(n)=1, f(n)=1/n, f(n)=1/n2
Sa se calculeze transformata Z inversa pentru functiile:
F(z)=![]() , F(z)=
, F(z)=![]() , F(z)=
, F(z)=![]() , F(z)=
, F(z)=![]()
Sa se calculeze transformata Laplace directa pentru functiile:
f(t)=e-4t+sin(t-2)+t2e-2t, f(t)=sin(at), f(t)=cos(at), f(t)=eatsin(bt)
Sa se calculeze transformata Laplace inversa pentru functiile:
![]() ,
, 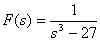 ,
, ![]() ,
, ![]()
Copyright © 2025 - Toate drepturile rezervate