Algoritmii si descrierea lor

Tema de casa

Algoritmii si descrierea lor

Notiunea de algoritm

are o vechime de mai mult de 2 milenii (apare inca de la Euclid) desi forma actuala a cuvantului provine de la numele matematicianului arab care l-a introdus in circuitul
european in evul mediu.

Scopul textului de fata este prezentarea cat mai clara a notiunii sirespectiv a conceptului mai ales prin prisma posibilitatilor de aplicabilitate de catre un utilizator de formatie tehnica generala.

Algoritmul este definit in [DEX98] drept un "ansamblu de simboluri folosite in matematica si in logica, permitand gasirea in mod mecanic (prin calcul) a unor rezultate.♦ P. gener. Succesiune de operatii necesare in rezolvarea unei probleme oarecare."

Modalitati logice de avans si exemple tipice

Pentru a explica mai clar aspectul esential, de "urmarire" a etapelor de rezolvare a unei probleme, mai adecvata pare utilizarea in context a sintagmei "modalitate logica de avans"! Aceasta defineste de fapt un algoritm.

Structuri fundamentale liniare

Structuri fundamentale alternative

Pentru exemplificare se va analiza o problema matematica simpla (abordata de obicei in cartile consacrate subiectului) : rezolvarea unei ecuatii de gradul al II-lea: a∙x²+b∙x+c = 0, pentru care se cunoaste relatia de calcul a solutiilor.

In Tabelul nr. III.4 se descrie algoritmul complet de rezolvare a ecuatiei de gradul 2, in cel mai general caz.

Tabelul nr. III.4

In tabel apar relatii cu operatorul de atribuire ( : = explicat detaliat la subcapitolul nr.III.4, lectia L.0.5.2). Toate celelalte reprezinta conditii (in care poate figura operatorul = cu rol relational) pentru salt.

In figura nr.III.23 acelasi algoritm este descris cu ajutorul limbajului simbolic, printr-o ordinograma.

Structuri fundamentale repetitive

Algoritmul A_CP_{0_1} contine referiri la lectia L.0. - prin CP(0) - si se continua cu referiri la competenta CP(1). In figura nr. III.5 est prezentata descrierea completa in limbaj simbolic a acestuia.

III.2.3 Definirea completa a conceptului de algoritm

In subcapitolul anterior au fost evidentiate aspectele esentiale care privesc conceptul de algoritm pe baza unor exemple simple. Concluziile (editate incadrat) au relevanta pentru realizarea unei definiri mai riguroase, cu scopul de clarificare, asa cum este prezentata spre exemplu in [Zah92].

Definitie

Prin algoritm se intelege o multime finita de operatii cunoscute, care se executa intr-o ordine bine stabilita, astfel incat, pornind de la un
set de date (datele initiale ale problemei) care indeplinesc anumite
conditii, se obtine, intr-un interval de timp finit, un set de valori:
rezultatul, reprezentand solutiile problemei.

Daca se asociaza definitiei si modalitatile de avans logic in succesiunea etapelor existente (posibile), prin cele 3 tipuri de structuri logice fundamentale: secventiale, alternative si repetitive, se poate spune ca s-a definit complet conceptul de algoritm. Cele trei structuri sunt asociate ades ([Don99]) cu cele trei cuvinte-cheie utilizate in referintele axate pe limbaje de programare: secventa, decizia si ciclul.

Descrierea algoritmilor

Introducere

Exista mai multe posibilitati de descriere a algoritmilor: in limbaj natural, apoi prin scheme logice (ordinograme), prin scheme structurale ("structurograme"), prin diagrame, prin tabele de decizie, cu pseudocod, cu limbaje speciale de descriere, etc.

Limbajul simbolic ( = schemele logice). Definire si blocuri constitutive

In manual se va utiliza descrierea de tip grafic cu ajutorul limbajului simbolic. Reprezentarile mai poarta denumirea de scheme logice, sau ordinograme.

Definitie

Prin schema logica se denumeste o reprezentare de tip grafic a
algoritmilor cu ajutorul unor figuri geometrice (denumite si
simboluri) a caror forma indica tipul actiunii care se executa in
etapa pe care o simbolizeaza. Figurile poarta denumirea de
blocuri. Blocurile sunt legate unul dupa altul, in ordinea executiei lor, prin segmente orientate. In interiorul lor se inscriu operatiile concrete din cadrul actiunii care urmeaza a fi executata.

Este vorba de cel mai des utilizate simboluri, care pot fi regasite drept obiecte grafice "prefabricate", la procesoarele de texte. In cazul procesorului Word/Microsoft Office, acestea se genereaza din submeniul Flowchart al butonului AutoShapes, de pe bara Draw. Tabelul nr. III.6 contine simbolurile uzuale, iar Tabelul nr. III.7 contine simboluri particulare pentru elementele de iesire.

In blocurile-simbol se pot inscrie:

pasii (etapele de parcurs ale) algoritmului sau

operatiile aferente fiecarei etape.

Un algoritm este descris - de la pornire la final - printr-un traseu reprezentat de segmente orientate care leaga blocuri (simboluri) de diverese categorii. Traseul poate avea una sau mai multe ramificatii, respectiv poate descrie grafic structurile logice fundamentale.

Forma generala a unei scheme logice

Regula de constructie a schemelor logice impune alcatuirea lor dintr-o inlantuire secventiala de module care au proprietatea fundamentala de a avea o singura intrare si o singura iesire. In interiorul modulelor se pot plasa structuri fundamentale logice (construite cu ajutorul blocurilor) de tip secventa, decizie sau ciclu, dupa caz (prezentate descriptiv in exemplele anterioare) astfel incat sa mentina proprietatea "o intrare - o iesire"!

Observatie

Modulele pot fi constituite deasemenea din proceduri a caror executie este gestionata prin mijlocirea unui nucleu care apeleaza grupuri de instructiuni in functie de necesitati. Dar modalitatea logica de functionare a grupurilor este determinata in ultima instanta tot de cele trei tipuri de structuri!

Structuri fundamentale logice in limbaj simbolic

Structurile fundamentale liniare (secventiale)

sunt oglindite prin activitatile din prima parte a algoritmului A_Ec2.

Structurile fundamentale alternative (de decizie)

sunt oglindite spre exemplu prin activitatile pasilor 6 - 9 a algoritmului A_Ec2.

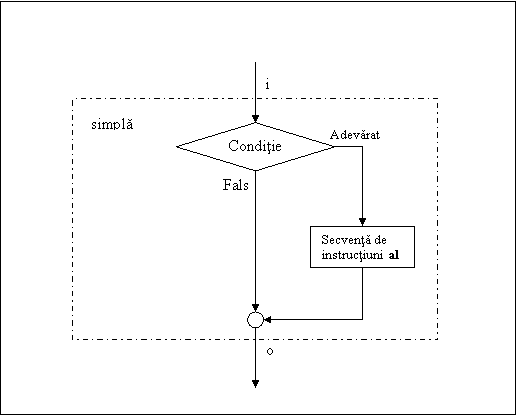
Se observa in figura nr. III.13 ca in blocul de decizie a unei astfel de structuri se

inscrie o conditie, a carei interpretare conduce algoritmul - prin raspunsul la intrebarea

"este adevarata conditia?" - spre una (si numai una!) din ramificatiile posibile ale

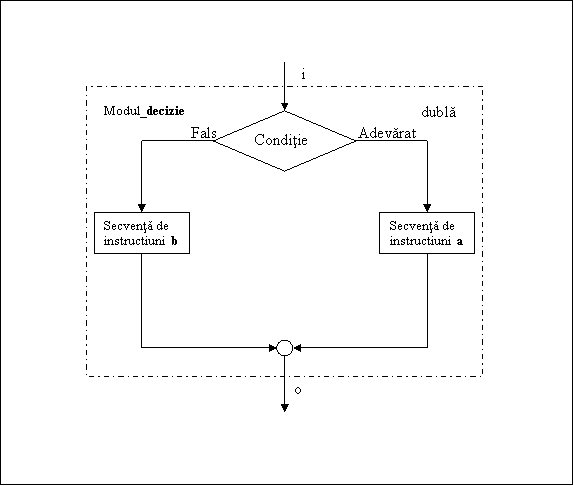
traseului de executie.

III.2.3.1.1            Structurile fundamentale repetitive (de ciclare)

sunt oglindite prin activitatile pasilor 16 - 18 a algoritmului A_Ec2. Sunt cunoscute si sub numele de "bucle" (in engleza "loop").

A. Tipuri functionale caracteristice

Structura contine o secventa (sau mai multe) de operatii care trebuie repetate dependent de indeplinirea unei conditii C determinate. Locul de dispunere a acesteia determina modul in care functioneaza structura, deasemenea si denumirea standard a acesteia! Exista 2 posibilitati functional diferite (indiferent de numarul de pasi de executat):

structuri repetitive conditionate anterior, de tip While-Do ("cat timp . executa . ", cuvinte-cheie care determina logica functionala a carei traducere contextuala in limbaj natural este: "cat timp C este adevarata executa secventa ")

structuri repetitive conditionate posterior, de tip Do-Until ("executa . pana cand . ", cuvinte-cheie care determina o logica functionala opusa celei anterioare, a carei traducere contextuala in limbaj natural este: "executa secventa pana cand C este adevarata ")

In figura nr. III.16 a) si b) se prezinta schemele logice ale celor doua tipuri de structuri fundamentale repetitive.

B. Sub-tipuri caracteristice (dependent de numarul de repetitii)

Se utilizeaza in context (pentru repetitii) termenul de "numar de pasi". Exista 2 subtipuri distincte de structuri de "ciclare":

cu numar necunoscut de pasi;

cu numar cunoscut de pasi.

Pentru a determina executia de un anumit numar de ori, n, a structurii, conditia din blocul de decizie este cea care trebuie legata de numarul de pasi de executat prin intermediul unei variabile-contor, care "ii numara". Numai astfel structura se incadreaza in cel de-al doilea subtip caracteristic.

Pentru subtipul cu numar cunoscut de pasi, se utilizeaza de cele mai multe ori structura While-Do. Preluand forma ei cea mai generala din figura nr. III.17 b), in exemplul din figura nr. III.18, se prezinta modul de implementare pentru un numar n de pasi de executat, variabila-contor fiind j. Se observa ca aceasta trebuie initializata inaintea structurii si incrementata (=se adauga succesiv valoarea 1) in interiorul ei!

La astfel de structuri se pot observa cele trei "ingrediente" care le pot pune in functie: initializarea, modificarea si incheierea unui ciclu repetitiv. Referitor la repetitii, se mai utilizeaza si termenul iteratii.

III.2.3.2       Alte aplicatii

III.2.3.2.1            Gruparea de operatii in proceduri; exemplu cu structuri alternative imbricate

Sa se creeze o schema logica pentru algoritmul de calcul al functiei urmatoare:

III.2.3.2.2            Variabilele indexate si tratarea lor cu structuri repetitive

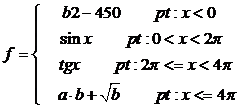
Un caz tipic pentru structurile repetitive este cel al lucrului cu variabilele indexate.

Algoritmul trebuie sa faciliteze transpunerea in limbaje de programare. Pentru valabilitate generala conform figurii nr. III.20 c), recomandate, se gestioneaza indexul printr - o variabila- contor care este argument al variabilei indexate din punct de vedere formal. Prin aceasta se pot introduce elementele (indiferent de numarul lor) printr-o singura structura repetitiva in care figureaza doar elementul generic (prin simbolurile variabila + index). Se mai observa ca se aplica de doua ori o astfel de structura: o data la intrare si o data la iesire, dupa operatiile impuse de aplicatia concreta la care se lucreaza. Aplicatia complexa Situatie_1.0 si respectiv de la lectiile de programare uzeaza de aceasta modalitate de tratare.

Trebuie evidentiat faptul ca atribuirea de valoare pentru elementele variabilei indexate poate fi efectuata si in alte modalitati decat prin operatia de citire: spre exemplu prin calcul.