Parametrii de stare ai stelelor

Parametrii de stare ai stelelor

Parametrii fizici sau parametrii de stare ai stelelor sunt elemente cu

ajutorul carora se pot caracteriza proprietatile stelelor.

Masa stelei ( M ) se exprima de obicei in mase Solare ( M_S = 1,989 10³⁰ kg ).

Masele stelelor variaza intre 0,05 M_S si 50 M_S , exceptie facand stelele masive, a caror masa este mult mai mare decat 100 de mase solare.

Compozitia chimica a stelei: se exprima prin proportia la un kilogram de materie a hidrogenului, heliului si a celorlalte elemente. Pentru atmosfera stelei compozitia chimica se determina din spectrul stelei iar pentru interiorul stelei se deduce teoretic din modelele de structura stelara.

Raza stelei ( R ) se exprima de regula in raze solare (R_S = 6,96 10⁸ m).

4. Luminozitatea stelei ( L ): reprezinta energia radiatiei totale emisa de stea in unitatea de timp, pe toata suprafata stelei, pe toate lungimile de unda si in toate directiile ( se mai numeste flux integral total si are sensul fizic de flux energetic).

L = 4π R² H,    unde H este fluxul integral al stelei;

[L]_SI = W = Js^-1

L_s = 3,826 10²⁶ W

Temperatura efectiva a stelei ( T_ef ) este temperatura unui corp negru care ar emite aceeasi cantitate de energie pe unitatea de arie, in unitatea de timp, ca si unitatea de arie a stelei, in unitatea de timp.

Daca aproximam steaua cu un corp negru, conform legii Stefan-

Boltzmann, avem:

H = σ T⁴ = σ T_ef ⁴

Spectrul stelei se determina pe baza unei clasificari empirice, de exemplu, clasificarea Morgan- Keenan ( M-K ), care tine cont de clasa spectrala a stelei ( conform clasificarii Harvard ) si de clasa de

luminozitate ( stralucire ).

Spectrele stelelor se deosebesc in functie de intensitatea radiatiei care depinde de temperatura si de lungimea de unda si de structura interna a stelei ( numarul, pozitia si forma liniilor spectrale ). Clasificarea Harvard este unidimensionala, deoarece tine cont doar de temperatura.

R - N

I

W - O - B- A- F- G -K - M

I

S

Stelele din clasele principale, sunt impartite ( cu exceptia celor din clasa

O ), in 10 subclase, notate de la 0 la 9; in interiorul unei clase,

temperatura variaza de la o subclasa la alta; stelele din clasele M, N, R,

S, au aproximativ aceeasi temperatura dar compozitii chimice diferite.

Clasele de luminozitate, sunt notate cu cifre romane, de la I la VII:

I : corespunde clasei stelare a supragiganticelor;

II : corespunde clasei stelare a giganticelor luminoase;

III : corespunde clasei stelare a giganticelor normale;

IV : corespunde clasei stelare a subgiganticelor;

V : stelele seriei principale;

VI : subpiticele;

VII : piticele

Clasificarea Morgan- Keenan , o clasificare bidimensionala, tine cont

de faptul ca spectrul stelei depinde atat de temperatura cat si de

luminozitatea stelei. Clasa spectrala si clasa de luminozitate, alcatuiesc

tipul spectral al stelei.

Densitatea medie a stelei ( ρ_med ) : in apoximatia unei forme sferice a stelei, este

ρ_med = 3 M / ( 4πR³) ; ρ_S = 1,41 10³ kg/m³

Acceleratia gravitationala la suprafata stelei ( g ), depinde de masa si de raza stelei conform relatiei :

g = k M / R² , unde k este constanta atractiei universale:

g_S = 274 m/s²

Productia medie de energie a stelei pe kilogram de materie, pe secunda, denumita si generare medie de energie a stelei ( ε_med ):

ε_med = L / M

ε_med,S = 2 10 ^{- 4} W/kg

Rotatia stelei, este determinata prin perioada de rotatie, exprimata in zile medii.

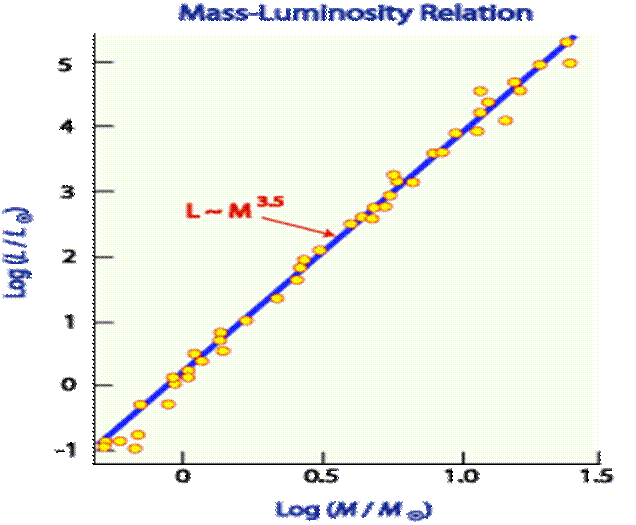
Masa stelei, compozitia ei chimica, raza si luminozitatea sunt

parametrii fundamentali. Conform teoremei Vogt - Russell, intreaga

structura interna a stelei si parametrii ei de la suprafata ( L, R ) sunt

complet determinati prin masa si compozitia ei chimica.

Intre parametrii de stare ai stelelor se stabilesc niste relatii empirice,

numite relatii de stare ale stelelor. O asfel de relatie este relatia

spectru - luminozitate ( diagrama Hertzsprung- Russel )

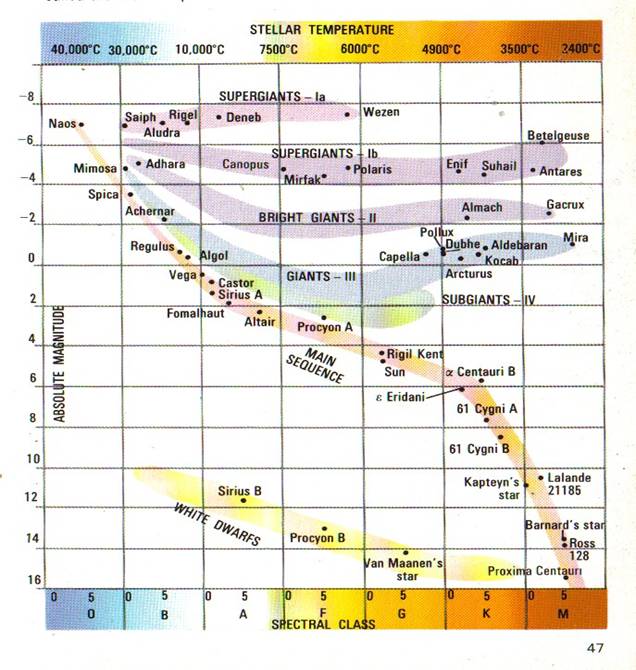
Determinarea maselor stelelor

La unele stele simple, masele se pot determina pe baza efectului Einsein de deplasre spre rosu a liniilor spectrale, datorita prezentei unui camp gravific intens. Dificultatea ce apare in acest caz consta in posibilitati limitate de separare a efectului Einstein de efectul Dopller, mai relevant la majoritatea stelelor; o separare buna a celor doua efecte s-a realizat la stelele pitice albe precum Sirius B si 40 Eridani B, la stele neutronice, quasari.

Δλ/λ = ( -Φ_e + Φ₀ )/ c² , Φ_e = potentialul gravitational in punctul de emisie

Φ_e = - kM/R ; M= masa stelei , R = raza

stelei

k = 6,67 10^-11 Nm²/kg²

Φ₀ = potentialul gravitational in punctul de

observatie

Φ₀ = kM_P/R_P ; Φ₀ este neglijabil in

comparatie cu Φ_e

Δλ/λ = ( -Φ_e )/ c² = kM/(R c²)

unde, R_g = 2kM/c² este raza gravitationala ( Schwarzschild)

Δλ/λ = R_g /(2R) ; pentru Soare, R_S = 0,696 10⁶ km iar R_g = 2,95 km

Valori precise pentru masele stelare furnizeaza stelele duble vizuale, pe baza legii a III-a a lui Kepler , aplicata sistemelor: Soare - Pamant si sistemului binar (T, m₁, m_{2 ,} a ).

T²_P (M_S + M_P) / a³_P = T² (m₁ + m₂) / a³ ; daca: T_P = 1 an, a_p = 1 UA, M_S = 1

atunci, avem pentru sistemul dublu : a³ /T² = m₁ + m₂ ;

Din masurari determinam semiaxa unghiulara a orbitei, a^" si paralaxa

sistemului π^"

a = r a^" / 206265^" iar r = 206265^" / π^" in UA , se obtine: a = a^" / π^"

m₁ + m₂ = a³ /T² = a^{" 3} / π^{" 3} T² , unde m₁ + m₂ este suma maselor

sistemului binar. Daca se cunoaste pozitia centrului de masa al

sistemului binar, CM, se cunosc distantele de la CM la cele doua stele,

a₁ si a₂ , si se pot determina masele celor doua componente:

m₁ a₁ = m₂ a₂ si a₁ + a₂ = a

La stelele duble spectroscopice si fotometrice , masele

componentelor se pot determina din curbele vitezelor radiale, v₁ si v₂

aplicand relatia:

m₁ v₁ = m₂ v₂ .

Determinarea temperaturilor stelare

O prima aproximatie a temperaturii stelei se face din tipul spectral, care

da temperatura de ionizare, ce poate fi corelata cu temperatura efectiva a

stelei.

Temperatura efectiva se determina in prima aproximatie din legile de

radiatie ale corpului negru valabile doar in conditii de echilibru

termodinamic. Pentru a determina exact temperatura stelei si distributia ei

cu adancimea, trebuie acceptat un anumit model de atmosfera stelara.

Determinarea temperaturii efective a stelelor, se poate face masurand cu bolometrul, stralucirea aparenta integrala ( E ). Bolometrul este un receptor termic care se bazeaza pe transformarea energiei radiante in caldura, care la randul ei determina o schimbare a temperaturii detectate de un termometru, ca o schimbare de rezistenta electrica.

E = R² σ T²_ef / r² , unde R = raza stelei iar r = distanta stea

observator

R / r = sin d/2 , unde d/2 este semidiametrul aparent al stelei si se

determina interferometric

T_ef = ( Er² / σ R² )^1/4 = [ E / (σ sin²d/2 ) ]^1/4

Sunt relativ putine stele la care E se poate determina bolometric iar d interferometric ( gigantele, Antares, Betelgeuse, etc.).

Alte metode de determinare a temperaturii stelelor:

a) determinand pozitia maximului in distributia energiei in spectrul continuu, utilizand legea lui Wien T λ_max = b ;

b) comparand distributia energiei in spectrul continuu cu izotermele lui Planck;

c) masurand stralucirea aparenta intr-un anumit domeniu de lungimi de unda si aplicand legea lui Planck:

E_λ = (R / r)² π F_λ , unde F_λ este fluxul mediu specific spre exterior

E_λ = (R / r)² ( 2πhc²/ λ⁵ ) [ 1 / ( e^hc/kTλ - 1)] , unde k este constanta lui Boltzmann iar T este temperatura monocromatica a stelei ( pentru o anumita λ ); pentru undomeniu mai largde lungimi de unda se integreaza pe tot domeniul si se obtine temperatura de radiatie.

d)     temperatura de culoare se determina di indicele de culoare pentru domeniul

vizual (pv) si cel fotografic(pg)

IC = m_pg - m_pv = f(T)

e)     din intensitatea liniilor spectrale, utilizand legea lui Boltzmann se afla

temperatura de excitare iar la utilizarea legii lui Saha se afla temperatura de ionizare.

Temperatura efectiva a stelelor este cuprinsa in domeniul 2000K , 100000K

Determinarea razelor stelelor

a) Metoda directa: utilizand relatia

R / r = sin d/2 , unde d/2 este semidiametrul aparent al stelei si se

determina interferometric, iar distanta stea observator,

r, se afla din paralaxa stelei;

R = r sin d/2 = d^" /(2 π^") in UA

Metoda se aplica doar la stelele la care semidiametrul aparent se poate

determina interferometric.

b) Metode indirecte:

Daca se cunosc luminozitatea si temperatura efectiva, se poate afla

raza stelei

L_{b, S} = 4π R²_S σ T⁴_ef,S ; L_b = 4π R² σ T⁴_ef

Din formula lui Pogson, raportul stralucirilor standard integrale ale stelei

si Soarelui , este:

E_st / E_st,S = L_b / L_{b, S} = 2,512 ^(M_S - ^M) ; M_S si M sunt

magnitudinile bolometrice absolute ale Soarelui, respectiv stelei.

2,512 ^(M_S - ^M) = ( R² / R²_S ) ( T⁴_ef / T⁴_ef,S ) ; logaritmand

aceasta expresie, se obtine:

M = M_S - 5 lg ( R/ R_S) - 10 lg (T_ef / T_ef,S ) ; daca R_S = 1, M_S =

4,7 si T_ef,S = 5780 K

M = 42,3 - 5 lg R - 10 lg T_ef ; cu R in raze solare si T_ef in

kelvin.

Din masuratori fotometrice intr-un anumit domeniu spectral:

E_λ = R² π B_λ(T) ; in aproximatia lui Wien la legea lui Planck,

B_λ(T) = (1/λ⁵) 2 h c² exp ( - h c/ k_B T λ) rezulta:

m_λ = C_λ - 2,5 lg E_λ

m_λ = C^'_λ - 5 lg R + 5 lg r + 2,5 hc lg c /( k_B T λ )

M_λ = m_λ + 5 - 5 lg r

M_λ = C_λ - 2,5 lg R + 1,56 / (T λ) ; C_λ se determina din conditia

ca relatia sa fie valabila pentru Soare penru care se cunosc din

observatii M si T pentru o anumita λ.

Pentru observatii fotometrice, in domeniul vizibil, avem:

M_V = - 0,18 - 5 lg R + 29500 / T_V unde T_V este temperatura

de radiatie in domeniul

vizual.

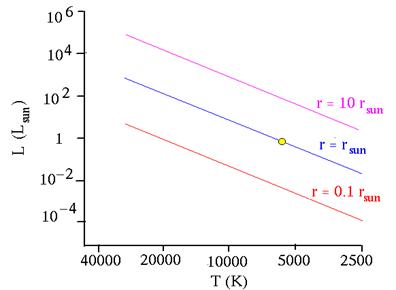
Determinarea luminozitatii stelelor (L_b)

a)     Metoda directa : daca se cunosc R si T_ef

L_b / L_{b, S} = 2,512 ^(M_S - ^M) = ( R² / R²_S ) ( T⁴_ef / T⁴_ef,S )

b)     Metoda indirecta

M - M_V = m - m_V = CB ; CB = corectia bolometrica

CB = 42,5 - 28400 / T_ef - 10 lg T_ef

Colegiul National "Vasile Alecsandri" , Bacau