Greutatea corpurilor - centrul de greutate al unui sistem de puncte materiale

GREUTATEA CORPURILOR

La suprafata Pamantului, corpurile sunt supuse atractiei acestuia. Asupra unui corp de masa m se exercita o forta, proportionala cu masa corpului, numita greutate.

(3.1)

unde , este acceleratia terestra si reprezinta rezultanta dintre acceleratia gravitationala (datorita fortei de atractie gravitationala) si acceleratia de transport (datorita miscarii de rotatie a Pamantului).

Valoarea acceleratiei terestre , variaza cu latitudinea si altitudinea, aceste variatii fiind relativ mici, in calcule se ia valoarea medie g = 9,81 m/s².

Tinand seama de raportul dintre dimensiunile corpurilor uzuale si ale Pamantului se poate considera ca greutatile corpurilor sunt forte indreptate dupa verticala locului, deci paralele intre ele. Din acest motiv, tratarea problemei greutatii sistemelor materiale reprezinta un caz particular al fortelor paralele, putandu-se utiliza rezultatele stabilite la acest capitol.

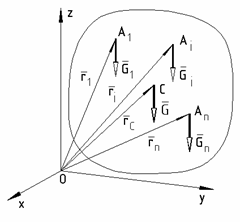
CENTRUL DE GREUTATE AL UNUI SISTEM DE PUNCTE MATERIALE

Fie un sistem de puncte materiale A_i de mase m_i si vectori de pozitie  in raport cu originea O a sistemului de axe.

Greutatea sistemului este:

(3.2)

si este aplicata intr-un punct definit ca centrul de greutate al sistemului, care este centrul fortelor paralele de greutate (fig.3.1).

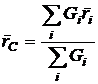(3.3)

Inlocuind relatia (3.2) in (3.3) obtinem:

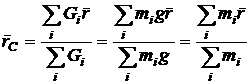(3.4)

ceea ce demonstreaza faptul ca centrul de greutate C este un element geometric, depinzand de modul de distributie a maselor din punctele A_i, fapt care justifica denumirea de centrul de masa.

Proiectiile pe axe ale vectorului  sunt coordonatele centrului de masa:

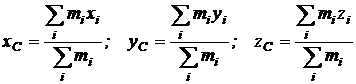(3.5)