 | Afaceri | Agricultura | Economie | Management | Marketing | Protectia muncii |
| Transporturi |
Problema de repartitie (de afectare)
O problema clasica de repartitie (afectare) este urmatoarea: fie n muncitori M1, M2, . ,Mn si n posturi de lucru P1, P2, . ,Pn. Fiecarei repartitii (Pi , Mj) ii este atasat un coeficient tehnic aij: aij 0, i, j = 1,2, . ,n (anumiti aij pot fi infiniti, ceea ce inseamna ca repartitia este imposibila).
Trebuie realizata repartitia celor n muncitori la cele n posturi de lucru in asa fel incat toti muncitorii sa aiba un singur post de lucru si numai unul, iar valoarea totala a repartitiei sa fie minima.
Se introduc variabilele echivalente:
![]()
![]()
Conditia ca fiecare muncitor sa fie repartizat la un singur post de lucru si conditia ca fiecare post de lucru sa fie repartizat unui singur muncitor se traduce prin restrictiile:
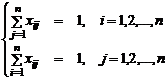
in care variabilele xij
satisfac cerinta speciala:![]() .
.
Obiectivul
urmarit, minimizarea valorii totale a repartitiei, se poate scrie: ![]() .
.
Problema afectarii este un caz particular al problemei de transport (problema de transport total degenerata). Ea nu se rezolva insa prin algoritmul problemei de transport, ci exista un algorit special, algoritmul Kuhn - Egélvary sau algoritmul ungar.
Vom prezenta algoritmul ungar pe un exemplu, pentru o mai usoara intelegere a acestuia.
Exemplu: Algoritmul ungar pentru determinarea unui cuplaj maxim de valoare optima
Fie A, B, C, D, E, F sase tineri programatori carora urmeaza sa li se incredinteze rezolvarea a sase tipuri de probleme a, b, c, d, e, f. Competentele lor fiind diverse, s-a notat cu pana la 100 aptitudinea fiecarui programator de a rezolva fiecare dintre problemele propuse. Aceste date sunt sintetizate in tabelul 1. Sa se gaseasca repartizarea optima pe probleme a celor sase programatori, astfel incat rezultatul final sa fie maxim.
Tabelul 1 Tabelul 2
|
a |
b |
c |
d |
e |
f |
a |
b |
c |
d |
e |
f |
||||
|
A |
A | ||||||||||||||
|
B |
B | ||||||||||||||
|
C |
C | ||||||||||||||
|
D |
|
D | |||||||||||||
|
E |
E | ||||||||||||||
|
F |
F |
Pentru a putea aplica algoritmul ungar, care determina repartitia optima de valoare minima, se construieste tabelul "pierderilor", scazand fiecare element al tabelului "castigurilor" (tabelul datelor initiale intr-o problema de maxim) dintr-un majorant al tuturor elementelor acestuia, de exemplu, pentru problema data, din aptitudinea maxima 100.
Tabelul obtinut (tabelul 2) este tabelul datelor initiale intr-o problema de repartitia optima de valoare minima, pentru determinarea caruia se poate aplica algoritmul ungar.
Etapa I. Se construieste matricea patratica M care are elementele:
![]()
Pentru exemplul ales: 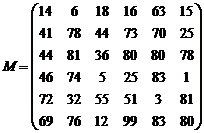
Etapa a II-a. Obtinerea cel putin a unui zerou pe fiecare linie si fiecare coloana.
Pasul 1 Pentru fiecare linie a matricei M se determina elementul minim, care se scade din toate celelalte elemente ale liniei respective; rezulta matricea M1.
Pasul 2 Pentru fiecare coloana a matricei M1 se determina elementul minim, care se scade din toate celelalte elemente ale coloanei respective; rezulta matricea M2.
Pentru exemplul dat, vom obtine succesiv matricele:
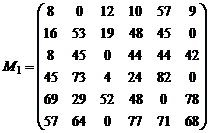
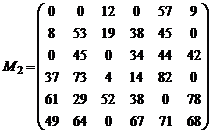
Etapa a III-a. Determinarea unei solutii optime
Pentru a afla o solutie optima trebuie sa afectam cat mai multor repartitii (i,j) din matricea M2 o valoare nula.
Daca in matricea M2 ar exista numai sase zerouri, astfel incat fiecare sa corespunda repartizarii unei singure probleme unui singur programator, aceasta ar fi solutia optima. Cum in matricea M2 exista mai multe zerouri, le vom deosebi astfel:
un "zerou incadrat" corespunde unei repartitii de valoare nula;
un "zerou barat" corespunde unei repartitii de valoare nula rezultata ca urmare a unei afectari anterioare;
un "zerou liber" corespunde repartitiilor neanalizate inca.
Se va proceda in felul urmator:
Pasul 1. In matricea M2, se alege linia care contine cel mai mic numar de zerouri, incepand de la prima linie (cea de sus) spre ultima linie.
Pasul 2. Se incadreaza primul zerou din linia retinuta si se bareaza celelalte zerouri de pe linia si coloana zeroului incadrat.
Pasul 3. Se reia etapa de la pasul 1 pana cand toate zerourile sunt fie incadrate, fie barate. In urma efectuarii etapei a II-a rezulta matricea M3.
In exemplul nostru, liniile a doua, a patra, a cincea si a sasea din matricea M2 au cate un singur zerou. Incepem cu linia a doua (prima de sus dintre ele): incadram zeroul de pe linia a doua si baram zeroul de pe coloana cu el (zeroul de pe coloana a sasea).
Linia a patra nu mai contine nici un zerou liber (a fost barat la pasul anterior) si continuam cu linia a cincea.
Incadram apoi zeroul de pe linia a cincea (nu avem ce alt zerou sa baram).
In final, incadram zeroul de pe linia a sasea si baram zeroul de pe coloana cu el (zeroul de pe coloana a treia).
In matricea M3 mai sunt inca zerouri libere, deci etapa se reia de la pasul 1.
Linia cu cel mai mic numar de zerouri libere este linia a treia (are un singur zerou). Incadram zeroul liniei a treia si baram zeroul de pe coloana cu el (zeroul de pe prima coloana).
Singura linie care mai are inca zerouri libere este prima linie. Din cele doua zerouri incadram unul si-l baram pe celalalt. Matricea M3 are forma finala:
![]() 0
0
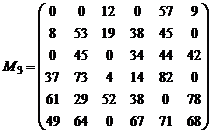
Deoarece nu s-au putut incadra decat 5 zerouri (pentru a gasi cuplajul maxim ar fi trebuit 6 zerouri incadrate, adica un numar egal cu ordinul matricei M) algoritmul continua.
Etapa a III-a. Marcarea liniilor si coloanelor
In aceasta etapa se va stabili numarul minim posibil de linii si coloane care sa contina toate zerourile incadrate sau barate ale matricei M3. Se va proceda astfel:
Pasul 1. Se marcheaza toate liniile care nu au un zerou incadrat;
Pasul 2. Se marcheza toate coloanele care au un zerou barat intr-o linie marcata;
Pasul 3. Se marcheaza toate liniile care au un zerou incadrat intr-o coloana marcata.
Pasul 4. Se reia etapa de la pasul 2 pana cand un alt marcaj nu mai este posibil.
In cazul exemplului dat vom avea:
se marcheaza linia a patra;
se marcheaza coloana a sasea;
se marcheaza linia a doua;
nu mai putem marca nici o coloana deoarece pe linia a doua, marcata la pasul 3, nu mai exista nici un zerou barat;
nu mai marcam nici o linie deoarece nu a mai aparut nici o coloana marcata.
Rezulta:
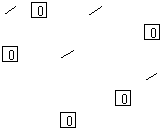
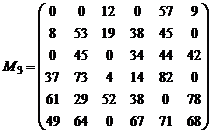
Pasul 5. Se taie liniile nemarcate si coloanele marcate:
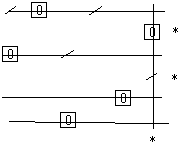
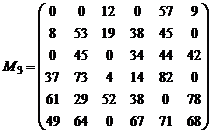
Pasul 6 In tabloul format numai din elemente netaiate, se alege elementul minim. Pentru exemplul luat, acesta este 4.
Pasul 7 Se scade elementul minim gasit la pasul 6 din elementele tuturor liniilor netaiate ale matricei M3. Restul elementelor raman neschimbate. Se obtine matricea M4 .
Pasul 8 In matricea M4, se aduna elementul minim gasit la pasul 6 la elementele coloanelor taiate. Restul elementelor matricei M4 raman neschimbate. Se obtine matricea M5.

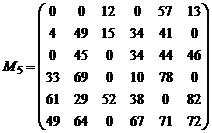
Pasul 9. Se reia algoritmul de la etapa a II-a. Dupa incadrarea si bararea zerourilor matricei M5 vom avea:
![]() 0
0
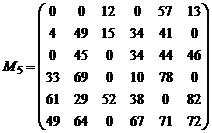
Nu avem sase zerouri incadrate, deci algoritmul continua cu etapa de marcare. Dupa marcare si taierea liniilor nemarcate si a coloanelor marcate, rezulta:
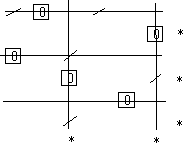
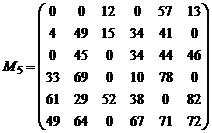
Elementul minim in tabloul de elemente netaiate de o linie sau coloana este 4. El se scade din elementele liniilor netaiate si apoi, in matricea rezultata, se aduna la elementele coloanelor taiate. Rezulta succesiv matricele M6 si M7 .
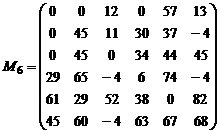
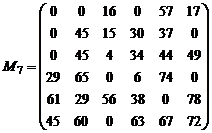
In matricea M7 se reia algoritmul de la etapa a II-a, etapa de incadrare si barare de zerouri.
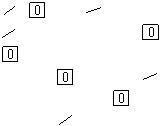
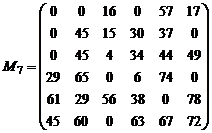
Nu s-a obtinut nici la aceasta iteratie solutia optima si algoritmul continua cu etapa a III-a, operatia de marcare a liniilor si coloanelor matricei M7 .
Se taie apoi liniile nemarcate si coloanele marcate. Rezulta:
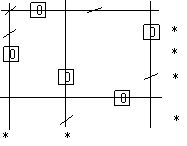
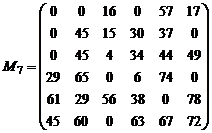
Elementul minim din tabloul cu elemente netaiate este 6. Se scade din elementele liniilor netaiate si, in matricea obtinuta, se aduna la elementele coloanelor taiate. Se obtin succesiv matricile:
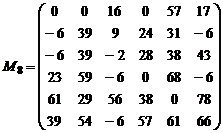
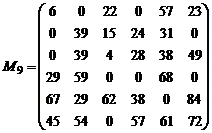
In matricea M9 se reia etapa de incadrare si barare de zerouri.
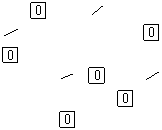
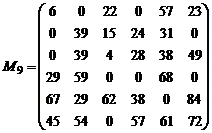
Deoarece s-au obtinut sase zerouri incadrate, s-a obtinut solutia optima ( Mopt ).
Folosind valorile arcelor corespunzatoare pozitiei zerourilor incadrate (din tabelul cu datele initiale ale problemei), se poate afla valoarea minima a cuplajului cautat.
Pentru exemplul luat, repartizarii optime a programatorilor pe problemele de rezolvat ii corespunde o aptitudine minima de 6 + 25 + 44 + 25 +3 + 12 = 115 (sau o aptitudine maxima de 600 - 115 = 485).
Copyright © 2025 - Toate drepturile rezervate
| Resurse-umane | |||
|
|||
|
| |||
|
| |||
|
|
|||