Analiza profitabilitatii asigurarilor de viata ("profit testing")

Analiza profitabilitatii asigurarilor de viata ("profit testing")

Procesul de tarifare a unei asigurari de viata presupune doua faze: cercetare si implementare. Prima faza insemna raspunsuri la multe intrebari de tipul "ce se intampla daca?". Se dezvolta astfel un produs ce inglobeaza o combinatie rezonabila de profitabilitate, compensare a agentilor de asigurare si competitivitate. Diferite variabile sunt modificate in scopul determinarii celei mai bune combinatii. Posibile variabile: comisioane pentru agenti, sume de rascumparare, excedente, prime s.a.. Aceasta faza este cea mai lunga si mai dificila. Se testeaza o varietate de scenarii; definirea clara a obiectivelor, experienta si intuitia joaca un rol important in limitarea scenariilor testate. Faza de implementare este mai rapida; se fixeaza aici pretul asigurarii.

Tehnica fluxului de numerar (cash-flow), aplicata in domeniul asigurarilor de viata, permite analiza profitabilitatii produselor. Se au au vedere diverse scenarii referitoare la variabilele implicate.

Referitor la active, vom presupune ca toate activele asiguratorului sunt purtatoare de dobanda. Activele asiguratorului sunt investite desigur si in active ce nu sunt purtatoare de dobada (actiuni, active imobiliare s.a.). Asiguratorul estimeaza rata dobanzii tinand seama si de rentabilitatea (sau lipsa rentabilitatii) acestor active.

In ceea ce priveste obligatiile (pasiv) vom presupune ca obligatiile asiguratorului constau doar in rezerve. Se presupune astfel ca daunele sunt platite imediat, primele sunt anuale, cheltuielile sunt platite imediat ce apar.

1. Tehnica cash-flow

Fluxuri de intrare: primele incasate, venitul din investitii.

Fluxuri de iesire: plati la deces/supravietuire (in general plata sumelor asigurate la aparitia riscului asigurat), cheltuielile asiguratorului, cresterea in rezerva.

Exemplu. Vom exemplifica modul de aplicare a tehnicii cash-flow pentru o asigurare mixta de viata. Presupunem ca asigurarea este subscrisa la varsta x de 28 de ani, durata asigurarii n este de 5 ani iar suma asigurata SA = 1 u.m.. Ipoteze utilizate in evaluarile actuariale:

ratele mortalitatii pe varste sunt conforme cu tabela de mortalitate 1990-1992 barbati;

rata anuala a dobanzii, utilizata in calculul primei si a rezervei matematice, respectiv rata rentabilitatii investitiilor asiguratorului i este egala cu 3,5%;

cheltuielile asiguratorului: α = 30%o din suma asigurata la incheierea asigurarii, β= 4% din prima bruta la inceputul fiecarui an de plata a primelor, γ = 5%o din suma asigurata la inceputul fiecarui an de asigurare.

Presupunem ca evolutia variabilelor implicate (mortalitate, dobanda, cheltuieli) in urmatorii 5 ani va fi conforma cu aceste scenarii. Portofoliul asiguratorului contine 100000 de contracte identice, de tipul precizat. Se cere:

a) fluxul de numerar aferent portofoliului, la sfarsitul fiecarui an de asigurare;

b) profitul generat de acest portofoliu, la sfarsitul fiecarui an de asigurare.

Rezolvare. a) Calculam pentru inceput prima bruta anuala a asigurarii:

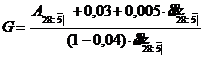
Deasemenea, calculam rezerva neta, la sfarsitul fiecarui an de asigurare. Evolutia acesteia este redata in tabelul urmator.

Tabel. Evolutia rezervei nete

Prima neta anuala:

.

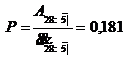Rezerva matematica neta la sfarsitul primului an:

.

In mod similar rezulta celelalte valori ale rezervei nete, indicate in tabelul 3.1.

Intrarile (+) respectiv iesirile (-) de numerar, aferente acestui portofoliu, sunt sintetizate in tabelul urmator.

Tabel. Fluxul de numerar si profitul pe portofoliu, la sfarsit de an de asigurare

Numarul politelor in vigoare la inceput de an se determina tinand seama de probabilitatile de supravietuire:

(3.1)

.

Venituri din prime

(3.2)

.

Cheltuieli de asigurare: anul 1

= (α + βG + γ )· l_x (3.3)

= (0,03 + 0,04 · 0,20045 + 0,005)·100000= 4302

in anii 2, 3, 4 respectiv 5 sunt prezente doar cheltuielile curente si cele de administrare

= (βG + γ ) · l_x+t-1    (3.4)

= (0,04 · 0,20045 + 0,005) · 99819 = 1299.

Veniturile din investitii

(3.5)

VI_t = (VP_t - ) · 0,035 = [(4)-(5)] · 0,035

VI₁ = (VP₁ - ) · 0,035 = (20045 - 4302) · 0,035 = 551.

Plati urmare a deceselor aparute, pe portofoliu:

(3.6)

.

Platile in caz de supravietuire se efectuaza doar la expirarea asigurarii:

(3.7)

.

Flux de numerar (cash-flow), la sfarsitul anului t, pe portofoliu: = VP_t+ VI_t - C_t - D_t - S_t sau

(3.8)

unde suma asigurata platita in caz de supravietuire la sfarsitul anului t este nula , pentru respectiv o unitate monetara la expirare.

= intrari - iesiri

b) Observam un flux de numerar (cash-flow) negativ, la expirarea asigurarii. Aici are loc o iesire substantiala de numerar, urmare a platii sumelor asigurate catre asiguratii ce au supravietuit pana la expirarea contractului.

Daca asiguratorul nu constituie rezerve pe parcursul anilor anteriori, atunci acesta nu va putea plati, la expirarea asigurarii, sumele asigurate. Devine astfel evidenta necesitatea constituirii rezervei matematice, in cazul asigurarilor mixte de viata.

Cresterea in rezerva reprezinta diferenta dintre rezerva de constituit, la sfarsitul anului (pentru supravietuitori), si rezerva deja constituita la inceput de an, fructificata cu dobanda:

(3.9)

Se utilizeaza valorile rezervei nete, din tabelul 3.1. Rezulta cresterea in rezerva pe portofoliu, la sfarsitul fiecarui an de asigurare:

.

La sfarsitul anului 5 nu mai este necesara constituirea unei rezerve (polita a expirat).

(9) Profitul pe portofoliu = (8) - (7)

= - (3.10)

respectiv

.

Profitul reprezinta partea ramasa din cash-flow dupa ce se retine suma necesara pentru constituirea rezervei. La sfarsitul primului an de asigurare, asiguratorul inregistreaza pierderi pe portofoliu. Aceste pierderi se datoreaza in principal cheltuielilor mari de achizitie aferente primului an.

Pentru asigurarile cu prime periodice, constante pe tot parcursul asigurarii, de regula se inregistraza pierderi in primul an, deoarece prima prima incasata nu este cu mult mai mare decat rezerva ce trebuie constituita. In primul an de asigurare, cheltuielile asiguratorului sunt substantiale, iar diferenta dintre prima de asigurare si rezerva nu acopera aceste cheltuieli.

Mentionam ca demersul anterior este adecvat si atunci cand prima anuala respectiv rata dobanzii utilizata in acumulare sunt variabile de la un al la altul.

2. Valoarea actualizata a profitului. Vectorul profit depinde de marimea rezervei constituite. Pentru calculul rezervei pot fi utilizate si alte baze tehnice (mortalitate, dobanda, cheltuieli) decat cele ce au stat la baza calculului primei de asigurare. In aceste evaluari de tip cash-flow intervin patru rate ale dobanzii (Hare & McCutcheon, 1991)

rata dobanzii utilizata in calculul primelor i_p

rata dobanzii ce intervine in calculul rezervei matematice i_r

rata dobanzii utilizata in calculul vectorului cash-flow si profit (aceasta fiind rata rentabilitatii investitiilor obtinuta de catre asigurator la investirea fondului de asigurare) i_v

rata dobanzii utilizata pentru actualizarea profitului r.

In simularile efectuate, aceste rate ale dobanzii nu trebuie sa fie egale respectiv pot varia de la un an la altul. In paragraful anterior s-a exemplificat modul de determinarea a vectorilor cash-flow respectiv profit pentru un portofoliu de polite identice, toate cele patru rate ale dobanzii fiind egale i_r =i_v = r = i_p (=3,5%).

Consideram un portofoliu format din asigurari mixte generalizate identice, incheiate la varsta x. Expresia (3.8) pentru fluxul de numerar precum si relatia (3.9) pentru profit pot fi extinse pentru cazul in care suma asigurata la deces respectiv supravietuire este variabila de la un an la altul (Hare & McCutcheon, 1991) :

(3.11)

respectiv

= (3.12)

unde:

reprezinta prima anuala bruta aferenta anului t, incasata la inceput de an

cheltuieli de gestiune pe polita in anul t, percepute la inceput de an

suma asigurata in caz de deces in cursul anului t, platibila la sfarsit de an

suma asigurata in caz de supravietuire a asiguratului la sfarsitul anului t

numarul de decese la varsta

reprezinta cresterea in rezerva in cursul anului t, pentru supravietuitori, adica suma ce se pune in contul rezervei la sfarsitul anului t.

Relatia (3.12) indica profitul generat de portofoliu, la sfarsitul fiecarui an de asigurare. Nivelul profitului depinde de fluxul de numerar dar si de rezerva matematica constituita. Aceasta abordare faciliteaza analiza influentei nivelului rezervei asupra profitabilitatii asigurarii. Mentionam ca uneori rezerva necesar a fi constituita, conform legislatiei, poate fi mai mare decat cea rezultata utilizand bazele tehnice din calculul primelor.

Profitul estimat pe polita in vigoare

Legatura dintre valoarea profitului evaluat pe polita in vigoare , la inceputul anului t, si profitul pe portofoliu , este redata prin relatia:

= l_x+t-1 · (3.13)

Avand in vedere relatiile (3.1) si (3.6), din (3.11) obtinem expresia fluxului de numerar pe polita in vigoare:

(3.14)

Deasemenea, din (3.12) rezulta expresia profitului pe polita in vigoare:

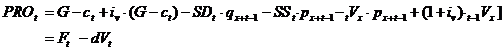(3.15)

unde este cresterea in rezerva pe polita.

Vectorul profit indica nivelul profitului (teoretic) obtinut de asigurator, la sfarsitul fiecarui an de asigurare, daca realitatea va fi conforma cu scenariile utilizate in calcul. Profitul este calculat, in baza relatiei (3.15), pentru fiecare polita in vigoare la inceputul anului t. Analiza profitabilitatii produsului se efectueaza in principal in faza de elaborare a produsului, fiind necesara evaluarea profitului pe polita subscrisa.

Profitul estimat pe polita subscrisa

Daca se imparte profitul pe portofoliu la numarul politelor subscrise obtinem profitul pe polita subscrisa PRO_t:

(3.16)

undeeste probabilitatea ca asiguratul, ce incheie asigurarea la varsta de x ani, sa supravietuiasca varstei x+t-1 (probabilitatea ca polita sa fie in vigoare la inceputul anului t). Acesta reprezinta profitul asteptat, pentru fiecare polita subscrisa, in ipotezele teoretice avute in vedere in analiza cash-flow.

Vectorul profit pe polita subscrisa poate fi obtinut si direct, in baza unui tabel similar cu tabelul 3.2. Se obtine in prima etapa vectorul profit pe polita in vigoare la inceput de an, conform relatiei (3.15), rezultand apoi vectorul profit pe polita subscrisa , din realatia (3.16).

Utilizarea metodei analizei fluxului de numerar in tarifare

In ipoteza egalitatii celor patru rate ale dobanzii ce intervin in analiza fluxului de numerar i_r =i_v = r = i_p , valoarea comuna fiind notata cu i, valoarea actualizata, la incheierea asigurarii, a vectorului profit pe polita subscrisa este zero (Hare & McCutcheon, 1991):

sau

(3.17)

unde este factorul de actualizare. Exista o relatie de echivalenta intre ecuatia (3.17) si ecuatia rezultata din principiul echivalentei, din tarifarea clasica.

Functie de profitul pe portofoliu, ecuatia (3.17) devine:

.

respectiv

(3.18)

Vom nota, in general, cu VAP valoarea actualizata a profitului pe polita subscrisa:

(3.19)

Prin urmare abordarea cash-flow poate fi utilizata si pentru calculul primei de asigurare in locul abordarii traditionale. Toate celelalte elemente fiind fixate, prima de asigurare G este singura necunoscuta din ecuatia (3.17).

Avantajele acestui mod de calcul al primelor, comparativ cu abordarea traditionala: se pot lua in considerare rate ale dobanzii variabile de la un an la altul, se poate tine seama de scaderea ratelor mortalitatii in timp, sumele asigurate in caz de deces respectiv supravietuire pot varia de la un an la altul respectiv pot fi luate in considerare, in tarifare, si alte elemente, precum: rascumpararile, inflatia (care are efecte in principal asupra cheltuielilor fixe pe polita).

In etapa de dezvoltare a unui produs de asigurare de viata se au in vedere o serie de aspecte, specifice fiecaruia din elementele ce stau la baza primei de asigurare. Privind mortalitatea:

asiguratorii tin seama si de experienta proprie

se are in vedere tendinta de evolutie pe termen lung a mortalitatii

se decide politica de subscriere (clasele de risc) si eventualele reasigurari necesare pentru riscurile majore.

Referitor la rata tehnica a dobanzii:

se are in vedere rata medie a rentabilitatii asiguratorului la activele sale, anticipata pe termen scurt si lung

se urmareste ca durata medie a obligatiilor sa fie aproximativ egala cu durata medie a plasamentelor activelor asiguratorului

se are in vedere rata dobanzii obtinuta dupa deducerea cheltuielilor legate de investitii.

Privind rascumpararile, taxele respectiv cheltuielile:

se are in vedere experienta proprie in privinta rascumpararilor

de regula suma de rascumparare variaza functie de momentul rascumpararii

pentru taxe si impozite se tine seama de legislatie

comisioanele de incasare se stabilesc astfel incat sa nu incurajeze rascumpararile

de regula comisionul de achizitie este mai mare, pentru a se tine seama de efortul de vanzare, iar comisionul de incasare are ca obiectiv asigurarea persistentei politei

se au in vedere statisticile asiguratorului privind cheltuielile, si influenta inflatiei asupra cheltuielilor.

Testele de senzitivitate pot avea in vedere modificarea nefavorabila a mortalitatii, a ratei tehnice a dobanzii, cresterea rascumpararilor, a ratei inflatiei, a cheltuielilor etc..

Exemplu. Reluam datele din exemplul anterior, tabelul 3.2.. Se cere: valoarea actualizata a profitului, utilizand pentru actualizare o rata a dobanzii egala cu 3,5% .

Rezolvare. Valoarea actualizata a profitului pe portofoliu:

Regasim rezultatul 3.19 respectiv principiul echivalentei din tarifarea clasica, valoarea actualizata a profitului obtinut de catre asigurator fiind nula, atunci cand cele patru rate ale dobanzii sunt egale.

3. Criterii utilizate in analiza profitabilitatii

Metoda analizei fluxului de numerar permite o serie de investigatii asupra unui portofoliu de asigurari de viata. Pentru diverse scenarii privind evolutia variabilelor implicate. se estimeaza vectorul profit, valoarea actualizata a profitului si se decide daca aceasta se incadreaza in asteptarile asiguratorului privind profitabilitatea produsului.

De regula in primul an de asigurare (chiar in primii 2-3 ani pentru asigurarile cu durata mai lunga) asiguratorii inregistreaza pierderi pentru majoritatea asigurarilor traditionale de viata cu prime esalonate. Rezerva minima ce trebuie constituita plus cheltuielile de achizitie si administrare nu sunt acoperite din prima anuala incasata. Suma necesara pentru acoperirea acestor pierderi provine de la un investitor (ex. actionarii), rata dobanzii r percepute de acesta pentru capitalul investit (costul capitalului) reprezentand rata dobanzii utilizata in actualizarea profitului. In analizele cash-flow specifice asigurarilor de viata, aceasta rata este intre 10% si 20%. In general, cu cat o investitie este considerata mai riscanta cu atat rata dobanzii r va fi mai mare. Prin urmare, pentru produsele de asigurare mai riscante rata de actualizate a profitului, considerata in evaluarile cash-flow va fi mai mare.

Ne intrebam in continuare daca un anumit tip de contract genereaza un profit acceptabil. Prezentam cateva din criteriile utilizate in analiza profitabilitatii asigurarilor de viata (Hare & McCutcheon, 1991).

1) Marja de profit reprezinta raportul dintre valoarea actualizata a profitului asteptat pe polita subscrisa si valoarea actualizata asteptata a primelor incasate, ambele actualizate cu aceeasi rata a dobanzii r:

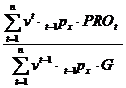(3.20)

unde este factorul de actualizare. Raportul indica ponderea profitului estimat in primele incasate. Produsul este profitabil daca marja de profit este mai mare decat o valoare minima (ex. 7%).

2) O alta masura se bazeaza pe timpul necesar pentru recuperarea capitalului investit (pentru acoperirea pierderii din primii ani de asigurare). Acesta trebuie sa fie mai mic decat o anumita valoare minima. Se determina anul incepand cu care valoarea actualizata a profitului VAP devine pozitiva, acesta fiind anul in care produsul incepe sa contribuie la "averea" asiguratorului:

(3.21)

3) Rata interna a rentabilitatii (RIR) este utilizata deasemenea ca masura a rentabilitatii unei investitii. Rata interna a rentabilitatii este rata dobanzii i pentru care vectorul profit pe polita subscrisa are valoarea actualizata egala cu zero VAP = 0. Nu intotdeauna ecuatia:

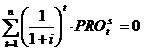(3.22)

sau echivalent

are solutii. Pentru luarea unei decizii, RIR poate fi comparata cu rata dobanzii utilizata in actualizarea profitului. Aceasta masura a profitabilitatii este utilizata in principal pentru asigurarile pe termen lung.

4) Necesarul de capital aferent primului an de asigurare este determinat in principal de marimea comisionului de achizitie. Pentru a se accepta lansarea produsului se poate cere ca raportul intre valoarea actualizata a profitului si comisionul de achizitie sa nu fie mai mic decat un anumit procent p (ex. 50%):

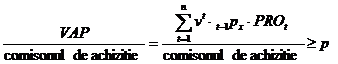(3.23)

Metodele traditionale de tarifare utilizeaza scenarii deterministe pentru previziunea profitabilitatii. Modelarea stochastica a ratei dobanzii respectiv a ratelor mortalitatii aduce informatii suplimentate privind variatia profitabilitatii produsului (riscul la care se expune asiguratorul).

Exemplu. Se considera datele din exemplul precedent. Rata anuala a dobanzii considerata adecvata pentru evaluarea fluxului de numerar si a profitului, pe parcursul celor 5 ani de asigurare, este de 11%.

Se cere:

a)     valoarea actualizata a vectorului profit pe polita subscrisa. Rata dobanzii utilizata in actualizare este de 12%;

b)     analiza profitabilitatii produsului prin prisma criteriilor cunoscute.

Rezolvare. a) Redam rezultatele obtinute pentru o rata anuala a dobanzii , rezervele si primele fiind calculate cu o rata a dobanzii de 3,5%.

Tabel. Profit pe polita subscrisa, pentru o rata a dobanzii

Fata de tabelul 3.2 intervin modificari in coloana (4) respectiv in coloana (8).

Veniturile din investitii VI_t = (VP_t - ) · 0,11 = [(4)-(5)] · 0,11

VI₁ = (VP₁ - ) · 0,11 = (20045 - 4 302) · 0,11 =1732.

(8) Cresterea in rezerva:

= l_x+t · - (1 + 0,11) l_x+t-1 · .

Coloana (10) respectiv (12) rezulta in baza relatiei (3.13) si (3.16).

b) Valoarea actualizata a profitului pe polita subscrisa, utilizand pentru actualizare o rata a dobanzii egala cu 12%, este:

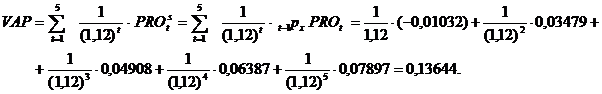
1) Marja de profit:

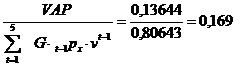
deoarece

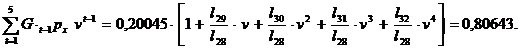
Daca s-a fixat ca si obiectiv o marja de profit de 10%, atunci produsul este profitabil, prin prisma acestui criteriu, deoarece 16,9 % > 10 %.

2) Pentru determinarea timpului necesar recuperarii capitalului investit, se determina valoarea actualizata a profitului degajat pana la sfarsitul anului t:

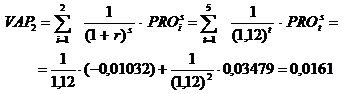
S-a considerat o rata de actualizare a profitului r = 12%. Capitalul necesar a fi investit, in primul an de asigurare, se va recupera treptat din profiturile generate in urmatorii ani. Incepand cu anul 2 valoarea actualizata a profitului devine pozitiva, astfel capitalul investit se recupereaza dupa 2 ani.

3) Rata interna a rentabilitatii reprezinta rata dobanzii pentru care valoarea actualizata a profitului este zero VAP = 0. In cazul nostru ecuatia:

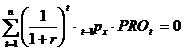
are solutia r = 3,01.

4) Cheltuielile achizitie sunt α = 30%o = 0,03. Daca se considera procentul p egal cu 50%, atunci produsul de asigurare este profitabil, prin prisma acestui criteriu, deoarece VAP = 0,1364 > 0,5 · 0,03.