OPERATORI GENETICI UZUALI CODIFICAREA BINARA

UNIVERSITATEA DIN ORADEA

FACULTATEA DE MEDICINA SI FARMACIE

SPECIALIZAREA: FARMACIE

OPERATORI GENETICI UZUALI

CODIFICAREA BINARA

I. Calculul evolutiv

Calculul evolutiv reprezinta o tehnica pentru rezolvarea unor probleme considerate ca fiind grele, din cele mai diferite domenii: stiinta, tehnica, economie, urbanistica, etc.

Din punct de vedere al ideilor de pornire si aplicatiilor Calculul evolutiv evidentiaza doua aspecte:

utilizeaza idei si concepte referitoare la sistemele adaptative complexe pentru a rezolva probleme computationale(in special de optimizare si cautare);

utilizeaza calculatoarele si metodele computationale pentru a modela sisteme adaptive complexe.

Calculul evolutiv este un corpus de concepte si metode, avand ca punct de pornire o metafora biologica. O populatie (aleatoare) de solutii initiale (cromozomi sau indivizi) este modificata prin operatori de tip biologic(selectie, incrucisare, mutatie, etc.).Procesul de modificare favorizeaza solutiile cele mai bune. Cei mai buni indivizi(cromozomi) vor fi selectati ca parinti ai unei noi generatii de solutii. In felul acesta calitatea solutiilor obtinute se imbunatateste. Cel mai bun individ obtinut intr-un numar fixat de generatii va constitui solutia finala a problemei.

II. Principiul selectiei

Scopul selectiei este de a asigura mai multe sanse de reproducere celor mai performanti indivizi dintr-o populatie data. Actiunea operatorului de selectie stabileste indivizii din populatia curenta ce vor contribui la constituirea generatiei urmatoare.

Pentru a realiza selectia este necesara introducerea unei masuri a calitatii (performantei, adecvarii) indivizilor. Prin selectie se urmareste maximizarea performantei indivizilor. Cautarea se concentreaza asadar in regiunile spatiului solutiilor ce corespund adecvarii maxime. Aceasta concentrare realizeaza exploatarea celor mai bune solutii gasite, ceea ce constituie sarcina selectiei.

III. Scalarea

Mecanismul de selectie proportionala este natural si are avantaje care devin mai evidente in teoria schemelor. Selectia proportionala are insa si unele dezavantaje. Daca populatia este foarte neomogena si exista un individ a carui performanta este mult superioara mediei, acest individ va fi selectat de mai multe ori si astfel el va constitui aproape exclusiv populatia urmatoare. In felul acesta, diversitatea populatiei se pierde si procesul de cautare nu mai exploreaza si alte regiuni ale spatiului, ceea ce antreneaza anumite riscuri legate de convergenta prematura a procedurii de cautare.

Daca exista diferente mici intre performantele indivizilor unei populatii, atunci probabilitatile de selectie devin aproximativ egale. Rezulta ca nu va mai avea loc o selectie veritabila (selectia stagneaza). Selectia obtinuta se va comporta mai degraba ca o alegere pur aleatoare. Uniformizarea performantelor antreneaza deci disparitia selectiei.

Cele doua situatii extreme: dominatia unui individ sau a unui numar mic de indivizi performanti si selectia cvazi-aleatoare, in care performanta indivizilor joaca un rol neglijabil, trebuie deopotriva evitate.

Vom considera doua solutii pentru ameliorarea selectei: una din ele consta in adoptarea unei transformari (schimbare de scala) a functei de performanta, astfel incat valoarea minima si cea maxima a functiei transformate sa atinga valorile dorite. Se poate alege o transformare liniara sau una exponentiala. Schimbarea de scala poate fi una statica (aceeasi pentru toate generatiile) sau una dinamica. In ultimul caz, scalarea functiei criteriu este repusa in discutie cu fiecare noua generatie (Baker, 1985). Prin schimbarea de scala , diferenta intre valorile functiei de performanta se poate modifica in sensul dorit.

IV. Selectia bazata pe ordonare

O alta idee de selectie consta in a calcula (pentru fiecare generatie ) valorile functiei de adecvare si de a aranja indivizii in ordinea descrescatoare a acestor valori. Se va atribui fiecarui individ i o probabilitate de selectie p_i ce depinde de rangul sau in sirul stabilit. In acest scop se utilizeaza presiunea de selectie.

Presiunea de selectie se defineste ca fiind numarul mediu de descendenti ai celui mai performant individ. Presiunea de selectie este o constanta a metodei. De regula presiunea de selectie se exprima printr-un numar q din intervalul

Fie n numarul de indivizi ai populatiei si r_i rangul individului i , probabilitarea de selectie pentru individul i se defineste ca fiind :

unde q este presiunea de selectie.

Aceasta strategie de selectie se numeste selectie prin ordonare. Putem observa ca probabilitatile de selectie depind acum doar de pozitia relativa a cromozomilor si nu de valorile functiei de adecvare. In acest fel se evita inconvenintele selectiei proportionale. Probabilitatea de selectie a primului cromozom, obtinuta punand r_i = 1, este:

Pentru individul ultim clasat, r_n = n, avem probabilitatea de selectie :

Numarul mediu de selectari ale individului i este n∙p_i.

Avand in vedere ca n∙p₁=q rezulta ca cel mai performant individ va fi selectat in medie de q ori .

Pentru ultimul cromozom avem n∙p_n=2-q.

Rezulta ca cel mai putin performant individ va avea in medie (2-q) selectari, deci un numar mediu de (2-q) descendenti.

Exemplu:

Se considera o populatie formata doar din doi indivizi. Daca alegem q=2 atunci selectia prin ordonare ne da p₁=1 si p₂=0. rezulta ca pentru populatia urmatoare va fi selectat doar primul cromozom. Daca q=1 atunci obtinem p₁=p₂=1/2, adica ambii cromozomi vor fi selectati in urmatoarea populatie.

Exemplul precedent ne permite sa stabilim o legatura intre doi factori extrem de importanti in cautarea genetica: diversitatea populatiei si presiunea de selectie. Cresterea presiunii de selectie orienteaza cautarea asupra celor mai performanti indivizi, determinand micsorarea diversitatii populatiei. Prin urmare, o presiune de selectie ridicata poate fi asociata cu o convergenta prematura a cautarii. O presiune de selectie scazuta poate duce la uniformizarea selectiei, cautarea de venit putin eficienta. Trebuie mentinut un echilibru intre diversitatea populatiei si presiunea de selectie. Putem interpreta acesata cerinta ca exprimand o alta fateta a ideii de echilibru explorare-exploatare.

Cresterea presiunii de selectie focalizeaza cautarea asupra celor mai performanti indivizii. Aceasta exploatare a celor mai bune solutii gasite este inotita de o pierdere a diversitatii genetice ceea ce antreneaza reducerea capacitatii de exploatare a spatiului starilor. Reducerea presiunii de selectie creste capacitatile de exploatare, deoarece in procesul de cautare vor fi inclusi mai multi cromozomi.

Mai sus s-a considerat un caz particular in care presiunea de selectie se exprima printr-un coefficient ce apare explicit in probabilitatea de selectie. Acest concent este mai larg si include diferite mecanisme de selectie.

Orice functie descrescatoare f : N→R, pote fi utilizata pentru o selectie bazata pe oronare. De exemplu, alegand un parametru h in intervalul (0,1) putem defini o probabilitate de selectie indusa de functie aneliniara:

f (i)= h(1-h)^i-1 , i=1,2, . , n.

In acest caz vom avea:

P_i=f(i), i=1,2, . ,n.

Aplicatia farmaceutica

Trizomia 18-Sindromul Edwards

Pentru a determina probabilitatea aparitiei Sindromului Edwards de la o generatie la alta intr-o populatie de n indivizi folosim indicatorii:

n=8 (numarul de indivizi)

r=3 (rang-generatie)

q=2 (presiunea de selectie)

Folosind ecuatia selectiei bazata pe ordonare si indicatorii enuantati anterior putem determina probabilitatea aparitiei Sindromului Edwards de la o generatie la alta :

P₁=

P₂=

P₃=

In concluzie : probabilitatea aparitiei Sindromului Edwards scade de la o generatie la alta.

V. Alte mecanisme de selectie

Ar putea fi interesant ca la fiecare generatie cel mai bun individ al unei populatii sa fie pastrat. O astfel de strategie se numeste elitista. Pare natural ca cel mai bun individ al unei generatii sa fie selectat ca un candidat pentru urmatoarea faza (cea de recombinare).

O alta idee este ca la fiecare generatie sa fie inlocuita doar o parte restransa a populatiei. Fie r un numar ce defineste rata de inlocuire. In cest caz se aleg rn indivizi ai populatiei. Cei rn descendenti ai indivizilor selectati ii vor inlocui pe parintii lor in noua populatie. O alta posibilitate este ca descendentii sa inlocuiasca alti indivizi din populatie si anume pe cei care sunt cei mai apropiati de ei. Daca cromozomi sunt codificati binar, apropierea cromozomilor poate fi calculata utilizand distanta Hamming.

Unele staregii de selectie sunt generationale, in sensul ca multimea parintilor este fixata pana cand noua generatie este completa. Alte strategii permit ca descendentii sa-si inlocuiasca parintii imediat ce noii cromozomi au fost generati.

Din alt punct de vedere strategiile de selectie pot fi anihilatoare sau conservatore. O selectie conservatore, spre deosebire de una anihilatoare, presupune ca fiecare individ are o probabilitate de selectie diferita de 0. in anumite strategii anihilatoare, pentru a apreveni convergenta prematura, se renunta la selectionarea celor mai buni indivizi ai populatiei.

Metodele de selectie pot fi dinamice sau statice. O selectie statica cere ca probabilitatile de selectie sa ramana constante de la o generatiei la alta (selectie prin ordonare). O selectie dinamica nu area o astfel de cerinta.

V.1. O selectie nestandard

Michalewicz (1992) a propus un mecanism de selectie ce alege in mod independent r cromozomi (nu neaparat distincti) pentru reproducere si r cromozomi distincti pentru stergere. Aceste selectii se realizeaza in functie de performantele cromozomilor. Un individ cu o performanta peste medie are o probabilitate mai mare de a fi selectat pentru recombinare. Cromozomii cu o performanta mai mica decat media au o probabilitate mai mare de a fi selectati pentru stergere.

Noua populatie P(t+1) este formata din (n-r) cromozomi din vechea populatie (toti din P(t) cu exceptia celor selectati pentru stergere) si r descendenti ai celor r parinti selectati. Sa notam ca fiecare cromozom selectat pentru modificare este utilizabil doar pentru o singura operatie genetica (mutatie, incrucisare, inversiune, etc.). Strategia prezentata este o metoda dinamica, generationala, conservatoare si elitista.

In urma selectiei apar trei populatii intermediare:

P₁ : contine cei r parinti

P₂ : contine r cromozomi ce vor fi strersi

P₃ : contine (n-r) cromozomi care vor fi copiati in P(t+1)

Populatiile P₁ si P₃ nu sunt neaparat disjuncte. Este posibil ca in populatia P (t+1) sa se gaseasca un cromozom cat si descendentii lui. Un cromoz avand o performanta peste medie poate fi selectat atat in P₁ cat si in P₃. In felul acesta, unul sau mai multi descendenti ai cromozomului respectiv vor intra in P(t+1). Daca se utilizeaza trei operatori (mutatie, incrucisare, inversiune), atunci asupra unei submultimi din P₁ se va aplica incrucisarea, asupra unei alte submultimi se va aplica mutatia si asupra celorlalti cromozomi din P₁ se va aplica operatorul de inversiune.

V.2. Selectia prin concurs

Selectia prin concurs sau selectia turnir ( tournament selection) se bazeaza pe compararea directa a cate doi cromozomi si selectarea celui mai performant. Operatiile implicate in acest tip de selectie sunt urmatoarele:

1. se aleg in mod aleator doi cromozomi.
2. se calculeaza adecvarile cromozomilor selectati.
3. cromozomul mai performant este selectat (copiat in populatia intermediara asupra caria vor actiona operatorii de recombinare si modificare) Pentru a genera o populatie intermediara formata din n cromozomi (copii nu neaparat distincte ale cromozomilor de la momentul t) este necesar ca mecanismul de scris sa fie aplicat de n ori.

VI. Probleme multimodale. Nisa ecologica

VI.1. Problema optimelor multiple

Multe probleme reale admit solutii multiple, care pot fi optimale sau aproape optimale. In anumite situatii suntem interesati nu doar de gasirea optimului global al unei probleme, ci si de multimea solutiilor acceptabile. Cunoasterea solutiilor optime multipleale unei problemene confera o anumita flexibilitate in alegerea dintre solutii alternative egal de bune, atunci cand acest lucru este necesar.

Intrebarea este cum putem face ca intr-o populatie sa coexiste o multime de solutii optimale. Acest lucru nu se realizeaza in mod automat deoarece populatia are tendinta de a converge spre un singur punct optim(chiar daca optimul global nu este unic).

Daca exista un optim global si mai multe optime globale populatia va evolua spere zona optimului global. Nu vor exista subpopulatii care, la convergenta, sa migreze spre zonele corespunzatoare optimelor locale.

Urmeaza ca pentru detectarea mai multor puncte de optim trebuie sa inzestram algoritmul genetic cu un mecanism suplimentar care sa favorizeze aparitia unor subpopulatii corespunzatoare diferitelor puncte de optim. O subpopulatie (ce corespunde unei specii) tinde sa ocupe o anumita zona a spatiului de cautare. Se contureaza astfel o analogie cu conceptual biologic de nisa ecologica .

Rezulta astfel ca pentru a obtine solutii optime simultane, indivizii unei populatii trebuie grupati in nise ecologice. Indivizii unei nise vor impartiti resursele acesteia. Astfel se exploateaza analogia cu nisele multiple existente in natura (oameni si animale) unde resursele nisei (hrana si pamant) sunt impartite intre populatiile ce ocupa nisa. Daca nisa este ocupata de o singura populatie, resursele sunt impartite intre indivizii acestei populatii.

Un exemplu din lumea vietuitoarelor, in acest sens, este ca fiecare specie ocupa o nisa ecologica, o anumita pozitie in cadrul unui ecosistem. Nisa este definita atat de parametri fizico-chimici ai mediului cat si de parametri biologici. Teoretic, doua specii nu pot ocupa in mod durabil aceeasi nisa ecologica. Selectia naturala tinde sa elimine speciile mai putin adaptate, invingator fiind cel mai bine adaptat, care reuseste sa se reproduca in modul cel mai eficient.

Specii diferite pot ocupa nise ecologice functional identice, dar in arii geografice diferite. Daca speciile conviatuiesc in acelasi areal, atunci nisele ecologice pe care le ocupa sunt diferite.

Pentru vietuitoarele parazite, acest mod de a trai, pe seama unui organism-gazda, nu inseamna altceva decat ca si-au gasit o nisa ecologica a lor. Cu adevarat impresionanta este diversitatea aspectelor pe care le poate imbraca acest fenomen.

VI.2. Functia de partajare

Intr-un algoritm genetic faptul ca indivizii unei nise trebuie sa imparta resursele acesteia, se traduce printr-o modificare a functiei de adecvare (potrivire). In acest scop se introduce o functie de partajare (Goldberg, Richardson (1987)) ce calculeaza gradul in care trebuie sa se faca impartirea resurselor intre doi indivizi ai populatiei. Ideea este ca indivizii apropiati vor trebui sa imparta in mare masura resursele deoarece ei apartin aceleiasi vecinatati (nise). Rezulta ca indivizii apropiati vor avea un grad de partajare mare. Reciproc, indivizii indepartati vor avea un grad de partajare mic.

O functie de partajare bazata pe distanta euclidiana realizeaza nise de forma sferica.

Valorile functiei de partajare vor depinde de distanta intre indivizi. Cu cat distanta inte indivizi este mai mare, cu atat valoarea corespunzatoare a functiei de partajare trebuie sa fie mai mica. Rezulta ca functia de partajare trebuie sa fie descrescatoare in raport cu distanta intre cromozomi.

Pentru a defini o functie de partajare consideram o distanta d peste multimea cromozomilor. Pentru o codificare binara a cromozomilor , d poate fi distanta Hamming (numarul pozitiilor in care cei doi cromozomi difera). In cazul in care genele se reprezinta prin simboluri ale unui alphabet finit poate fi utilizata distanta Levenstein. Definim distanta Levenstein dintre doi vectori (siruri, cromozomi) ca fiind numarul de stergeri, inserari (adaugiri) sau modificari effectuate asupra elementelor unui vectoe pentru a-l face identic cu celalalt. Distanta dintre cromozomi poate fi si norma iferentei intre punctele din spatiul starilor corespunzatoare celor doi cromozomi.

Putem defini functia de partajare ca fiind o aplicatie s:R→[0,1]. Daca doi cromozomi sunt identici , atunci gradul de partajare corespunzatoe este maxim. Gradul de partajare tinde la zero cu cresterea la infinit a distantei. Rezulta asadar ca functia de partajare trebuie sa satisfaca urmatoarele axiome:

s este descrescatoare;

,

Exemple:

O functie s care satisface axiomele unei functii de partajare este

Unde k > 0 este o constanta reala.

In acest caz gradul de partajare intre indivizii x_i si x_j este

s( d(x_{i ,}x _j)) reprezinta gradul de pertajare dintre x_i si x_j.

O functie de partajare simpla si intuitiva este:

O abordare mai realista se poate obtine admitand ca maximul distantei pentru care valoarea functiei de partajare este zero este un parametru al algoritmului. Fie a acest parametru, avand semnificatia de diametru al nisei (diametrul este distanta maxima dintre doi cromozomi pentru ca ei sa mai poata fi considerati in aceeasi nisa). In acest caz functia criteriu poate avea forma

VI.3. Functia de evaluare partajata

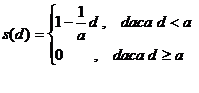
Pentru fiecare individ x_i din populatie se calculeaza marimea m_i avand expresia:

Interpretam m_i drept valoarea nisei corespunzatoare lui x_i. O alta posibilitate este ca suma ce intervine in expresia lui m_i sa nu se ia in raport cu intreaga populatie, ci doar in raport cu o subpopulatie. Semnificatia lui m_i este si de partajare totala a lui x_i.

Functia de evaluare f se va modifica folosind cantitatea m_i. Rezulta o functie de evaluare (adecvare) partajata f a carei expresie este:

VI.4. Mecanismul de selectie bazat pe nisa ecologica

In mecanismul de selectie adecvarea individului x_i va fi f^*(x_i). Utilizarea functiei de evaluare modificate f^* permite coexistenta solutiilor optimale (locale si globare) multiple. Acest lucru se explica in felul urmator. Sa admitem ca exista multi indivizi in vecinatatea lui x_i. Pentru toti indivizii din vecinatatea (nisa) respectiva utiliyarea functiei f^* va determina o crestere a valorii de adecvare. Aceasta descrestere reciproca a gradului de adecvare reprezinta un mecanism ce limiteaza dezvoltarea necontrolata a populatiei ce ocupa nisa respectiva.

Putem identifica o specie cu o zona de concentrare a indivizilor. Mecanismul propus limiteaza dezvoltarea spaciilor existente, permitand si aparitia altor regiuni de concentrare. Exista astfel sansa ca populatia sa evolueze spre regiuni corespunzand tuturor punctelor de optim.

Consideram ca intr-o generatie exista foarte putini indivizi corespunzand unei anumite solutii optimale. Fie S multimea acestor indivizi. Pentru o valoare potrivita a parametrului a distantele intre cromozomii multimii S vor fi mai mici decat a. Rezulta ca, de regula, este satisfacuta inegalitatea:

Distantele la indivizii care nu sunt in S vor fi, in general, mai mari decat valoarea paramertului a. Asadar, de regula, vom avea:

si deci

In valoarea m_i a nisei pentru cromozomul x_i din S contributiile nenule vor fi date, in general, de indivizii multimii S. Dar acesti indivizi sunt putini. Rezulta ca valorile lui m_i pentru indivizii din S vor fi mici in comparatie cu valorile corespunzatoare altor puncte de optim. Valorile functiei de adecvare partajata f^* vor fi mai mari pentru indivizii din S. Vor exista deci mai multi indivizi corespunzand acestui optim in noua generatie. Asadar optimul pe cale de disparitie (cu foarte putini reprezentanti intr-o populatie) va fi intalnit in generatia urmatoare prin utilizarea functiei de evaluare partajate. Acest mecanism simplu explica modul in care partajarea favorizeaza mentinerea in populatie a reprezentantilor diferitelor puncte de optim.