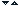 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
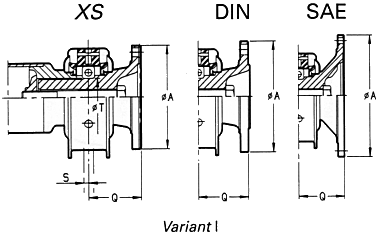
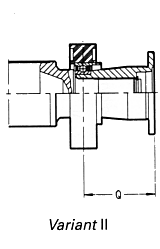
Variante de asamblare
Pentru a atasa transmisiile cardanice la mecanisme de transmisie si
osii sunt necesare diferite tipuri de asamblǎri. Sunt disponibile
urmǎtoarele tipuri de flanse (standard ISO): XS
|
|
Flansǎ cu angrenare pozitivǎ (Positive engagement) |
|
|
|
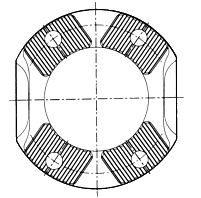
DIN
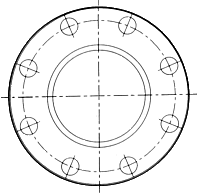 SAE
SAE 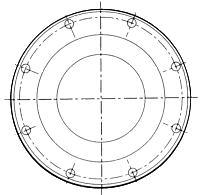
Flansa cu danturǎ in x (XS) este utilizatǎ tot mai mult datoritǎ avantajelor sale tehnice si economice si va fi preferatǎ in viitor.
Avantajele acestui tip de flansǎ sunt:
![]() (Positive engagement of serrations) Angrenarea
pozitivǎ a danturii
(Positive engagement of serrations) Angrenarea
pozitivǎ a danturii
![]() Necesitǎ
un timp mai scurt de montare
Necesitǎ
un timp mai scurt de montare
![]() Sistemul
de fixare cu suruburi este simplificat
Sistemul
de fixare cu suruburi este simplificat
![]() Se
utilizeazǎ mai putine suruburi
Se
utilizeazǎ mai putine suruburi
![]() Complexitate
redusǎ a . (Reduced stock complexity)
Complexitate
redusǎ a . (Reduced stock complexity)
![]() Pozitia
de asamblare este clar definitǎ
Pozitia
de asamblare este clar definitǎ
![]() Se
utilizeazǎ piulite cu blocare automatǎ Use of
self-locking nuts
Se
utilizeazǎ piulite cu blocare automatǎ Use of
self-locking nuts
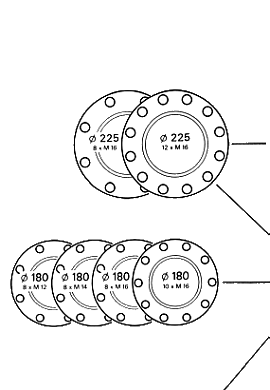
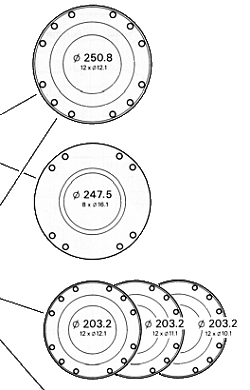
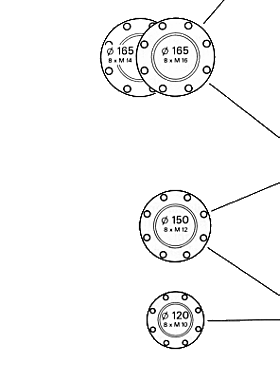
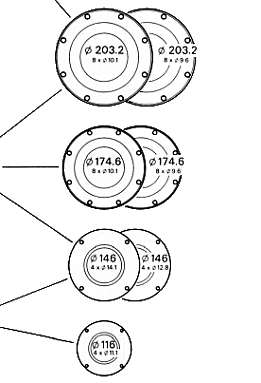
Numǎrul variantelor de flanse
|
10 Flanse DIN |
4 Flanse cu danturǎ in x ISO 12667 |
12 Flanse SAE |


Variante si combinatii de transmisii cardanice Variantele principale sunt:
Transmisie cardanicǎ cu compensare axialǎ
(fixǎ si mobilǎ) 
Transmisie cardanicǎ fǎrǎ compensare
axialǎ, cu cuplu maestru/imbunǎtǎtit
(Cardan shaft without length compensation with
midship)
(fixǎ si de mijloc) 
Transmisie cardanicǎ cu cuplu scurt / intermediarǎ si
compensare axialǎ (Short coupled cardan
shaft with length compensation)
variants with
sleeve yoke/sleeve muff
sleeve= manson, bucsa, mufa, tambur, cilindru, stut, niplu, cuzinet]
yoke = furca, travee, etrier, colier, brida
muff = cuplaj, manson, bucsa
Designul liniei de transmisie cardanicǎ poate varia in functie de
utilizare, de exemplu:

Ansamblu de arbori cu ax central de lungime fixǎ
si transmisie cardanicǎ cu compensare axialǎ Shaft assembly with fixed-length midship shaft and cardan shaft with length compensation

Ansamblu de arbori cu compensare axialǎ
si suprafatǎ de reazem centralǎ Alte variante disponibile la
cerere. Shaft assembly with
length compensationin midship bearing area Additional variants on request.
|
Variante speciale- ex: |
Nu necesitǎ intretinere, temperaturǎ crescutǎ/scǎzutǎ, constructie cu izolatie fonicǎ etc. la cerere. |
Arbori cardanici cu compensare axialǎ
Arbori cardanici
fǎrǎ compensare axialǎ cu cuplu central Cardan
shaft without length compensation with midship
Ansamblu de arbori cu compensare axialǎ in suprafata de reazem centralǎ Shaft assembly with length compensation in midship bearing area
Arbore cardanic intermediar
cu compensare axialǎ Short coupled cardan shaft with length compensation Design Cilindru - Furcǎ Sleeve-Yoke-Design
Arbore cardanic intermediar
cu compensare axialǎ Short coupled cardan shaft with length compensation Design Cilindru Bucsǎ Sleeve-Muff-Design
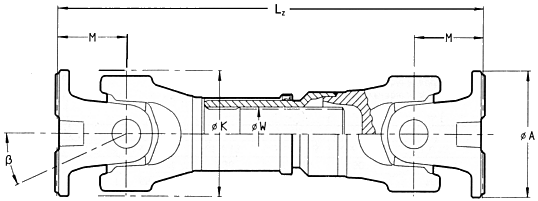
Arbore cardanic cu compensare axialǎ si articulatie
dublǎ pe ambele pǎrti Cardan
shaft with length compensation and centred double joint on both sides
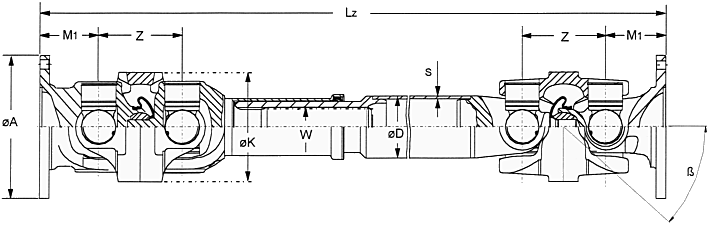
Arbore cardanic cu compensare axialǎ si articulatie
dublǎ pe o singurǎ parte Cardan shaft with
length compensation and centered double joint on one side
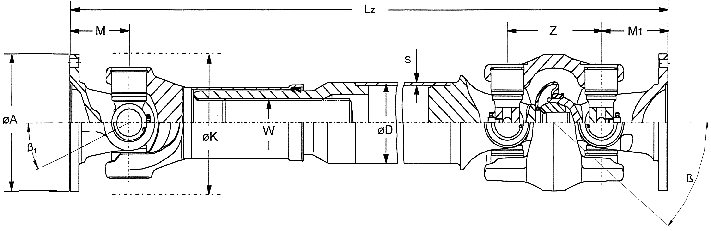
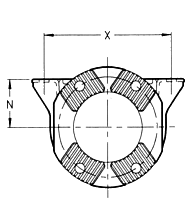
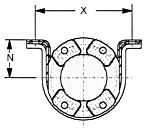
Flanse de asamblare - model X Serration flange fittings (XS)
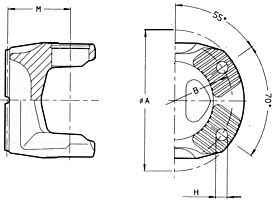
Flanse de asamblare - model DIN
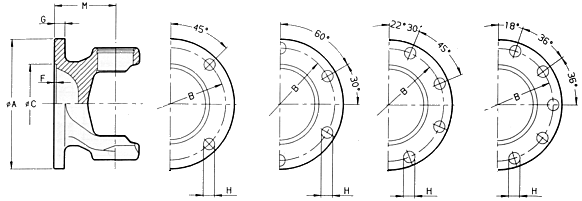
Flanse de asamblare -
model SAE
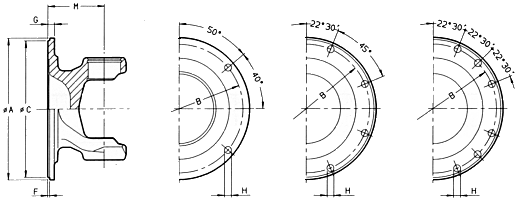
Rulmenti
intermediari
Cinematica
articulatiilor Hooke
1. Articulatiile
In cadrul teoriei mecanicii articulatia cardanicǎ, numitǎ
si articulatia Hooke, este definitǎ ca fiind o unitate de
actionare spatialǎ sau sfericǎ cu raport de transmisie
neuniform. Modul de transmisie al acestei articulatii este descries prin
ecuatia urmǎtoare:
the
theory of mechanics the cardan joint or Hooke's joint is defined as a spatial
or spherical drive unit with a non-uniform gear ratio or transmission. The
transmission behaviour of this joint is described by the equation.
![]()
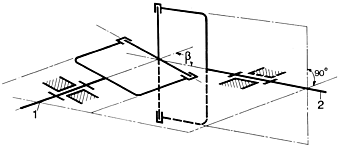
In aceastǎ ecuatie ![]() reprezintǎ momentul unghiului de
rotatie al axului 2. Miscarea capetelor antrenante si a celor
antrenate este descrisǎ in diagrama de mai jos. Miscarea
asincronǎ si / sau omocinematicǎ
a axului 2 este descrisǎ prin oscilarea periodicǎ a liniei
asincronice
reprezintǎ momentul unghiului de
rotatie al axului 2. Miscarea capetelor antrenante si a celor
antrenate este descrisǎ in diagrama de mai jos. Miscarea
asincronǎ si / sau omocinematicǎ
a axului 2 este descrisǎ prin oscilarea periodicǎ a liniei
asincronice ![]() in jurul liniei sincronice
in jurul liniei sincronice ![]() (linia intreruptǎ).
(linia intreruptǎ).
In this
equation ![]() the
momentary rotation angle of the driven shaft 2. The motion behaviour of the
driving and the driven ends is shown in the following diagram. The asynchronous
and / or non-homokinematic running of the shaft 2 is shown in the periodical
oscilation of the asynchronous line
the
momentary rotation angle of the driven shaft 2. The motion behaviour of the
driving and the driven ends is shown in the following diagram. The asynchronous
and / or non-homokinematic running of the shaft 2 is shown in the periodical
oscilation of the asynchronous line ![]() round
the synchronous line
round
the synchronous line ![]() (dotted
line).
(dotted
line).
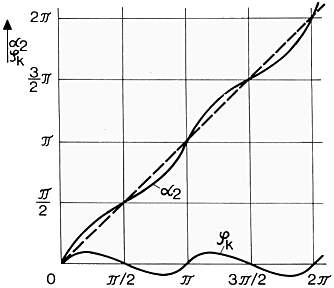
O valoare a neuniformitǎtii este datǎ de diferenta dintre
unghiurile de rotatie ![]() si
si ![]() sau raportul de transmisie dintre vitezele
unghiulare
sau raportul de transmisie dintre vitezele
unghiulare ![]() si
si ![]() .
.
A
measure for the non-uniformity is the difference of the rotation angles ![]() and
and
![]() or
the transmission ratio of the angular speeds
or
the transmission ratio of the angular speeds ![]() and
and
![]() .
.
Pusǎ in ecuatie, inseamnǎ: a) diferenta unghiului de
rotatie
Expressed
by an equation, that means: ![]()
![]() a) rotation angle difference
a) rotation angle difference
![]()
(numitǎ si eroare cardanicǎ)
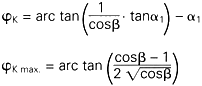
b) Raportul de transmisie
![]()
2. Arborele universal
Diferenta unghiului de rotatie ![]() sau eroarea cardanicǎ a unui arbore
universal curbat
sau eroarea cardanicǎ a unui arbore
universal curbat
poate fi compensatǎ in anumite conditii de instalare cu ajutorul altui arbore universal. Solutiile constructive sunt urmǎtoarele:
The rotation angle difference ![]() or
the gimbal error of a deflected universal joint can be offset under certain
installation conditions with a second universal joint. The constructive
solutions are the following:
or
the gimbal error of a deflected universal joint can be offset under certain
installation conditions with a second universal joint. The constructive
solutions are the following:
1) Unghiurile de curbare ale ambilor arbori trebuie sǎ fie egale,
adicǎ:
The deflection angles of both joints must be equal, i.e.
Existǎ douǎ posibiliǎti de montare: Two arrangements
are possible:
2) Cei doi arbori trebuie sǎ se afle in relatie unghiularǎ
cinematicǎ de 90° (![]() / 2), adicǎ furcile arborelui de legǎturǎ sǎ se afle in
acelasi plan.
/ 2), adicǎ furcile arborelui de legǎturǎ sǎ se afle in
acelasi plan.
The two
joints must have a kinematic angular relationship of 90° (![]() / 2), i.e. the yokes of the connecting shaft are in one plane.
/ 2), i.e. the yokes of the connecting shaft are in one plane.
Pentru un studiu mai amǎnuntit al cinematicii arborilor universali puteti consulta recomandarea 2722 a VDI (Asociatia Inginerilor Germani), literatura tehnicǎ relevantǎ si mai ales cartea ,,Kardangelenkgetriebe und ihre Anwendung' (Actionǎrile arborilor cardanici si aplicatiile acestora) scrisǎ de Florian Duditza si publicatǎ de VDI.
For a more intensive study of universal shaft kinematics we refer you to the VDI-recommendation 2722 to the relevant technical literature and especially to the book ,,Kardangelenkgetriebe und ihre Anwendung' (Cardan joint drives and their application) by Florian Duditza, published by VDI.
General
technical terms of propshaft application
Pentru a utiliza arborii din seria Compact 2000 s-au creat o metodǎ de
calcul si un software speciale. Aceastǎ metodǎ de calcul se
bazeazǎ pe termeni fizici generali si mǎsurǎtori effectuate
pe vehicule reale.
For the
application of propshafts of the series Compact 2000 a special calculation
method and software has been developed. This calculation method is based on
general physical terms and additional experiences of real vehicle measurements.
Termenii fundamentali ai metodei "VAMP" (Metodǎ de aplicare a arborilor la
vehicule) se referǎ la:
The
fundamental items of the 'VAMP-method' (Vehicle Application Method
for Propshafts) reflect to:
![]() parametrii
vehiculului
parametrii
vehiculului
![]() conditiile
de operare
conditiile
de operare
![]() valorile
caracteristice ale arborilor din seria Compact 2000
valorile
caracteristice ale arborilor din seria Compact 2000
![]() cerintele
speciale ale clientilor
cerintele
speciale ale clientilor
Astfel, se verificǎ urmǎtorii parametrii:
Criteria for fatigue strength is the maximum generated torque in the driveline under normal operating conditions.
|
a) cuplul motor maxim |
|
|
b) momentul maxim de aderentǎ the maximum adhesion torque |
In relation to the relevant criterion the size of propshaft with the sufficient static capacity Tcs is determined. Up to this torque limit a shaft can be loaded without disturbing the function of the driveline.
The structural strength is based on the maximum torque which can occur under extreme conditions or misuse. Limitations which refer to the adhesion torque are also taken into account.
|
- |
Relatia de vitezǎ maximǎ din timpul utilizǎrii ? the relation of the maximum speed during |
|
- |
Excitarea vibratiilor de torsiune generate de viteza arborelui si unghiul de lucru the excitation of torsional vibrations generated by propshaft speed and working angle |
In cele din urmǎ se va recomanda mǎrimea optimǎ a arborelui.
Pentru a identifica valorile
caracteristice specifice, de exemplu comportamentul dinamic special al
tansmisiilor, putem sprijini clientii prin efectuarea de simulǎri
si mǎsurǎtori ale vehiculului.
To identify specific characteristical values of e.g.
special dynamic behaviour of drivelines we can support the customers with
simulation calculations and vehicle measurements.
Vǎ rugǎm sǎ contactati expertii nostri in
aplicatii pentru orice alte probleme.
Cum se pot solicita informatii sau depune comenzi
Procesarea solicitǎrilor de informatii si a comenzilor de arbori
cu articulatii universale va fi mai usoarǎ si mai
rapidǎ dacǎ ne oferiti informatii referitoare la:
|
Conditii de
instalare
In timp ce se roteste articulatia universalǎ are While rotating, the universal joint has a
sinuslike, fluctuating angular speed depending on the deflection angle. As
described in detail in the chapter ,,General fundamental theory', this
system-linked fault can be offset for a driving line equipped with two or more
joints by choosing special joint arrangements.
When dimensioning the drive or the auxlliarv drive, the following rules
must be observed in practice:
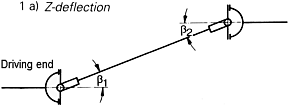
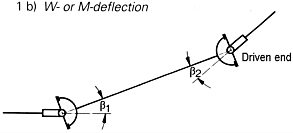
Angle conditions of the universal shaft
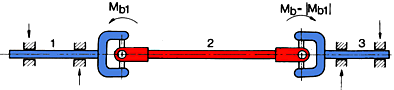
1. Ax cu douǎ articulatii Shaft with two joints
|
|
|
|
![]() The
deflection angles of the joints must be equal:
The
deflection angles of the joints must be equal: ![]()
![]() =
=
![]()
![]() This
rule is also applicable to front view and top view pictures.
This
rule is also applicable to front view and top view pictures.
![]() The
joint yokes of the connecting shaft must be in one plane.
The
joint yokes of the connecting shaft must be in one plane.
![]() All
three shafts must be in one plane.
All
three shafts must be in one plane.
Note: All these three rules must be observed simultaneously.
A joint arrangement in two planes must be avoided if possible. lt is always
given when the driving and driven shafts are not in the same plane. If this
arrangement is unavoidable and rigid on the installation side, this
,,fault' can be kinematically compensated by a joint misalignment.
|
|
|
|
For the resulting deflection angles the following equations are applicable:
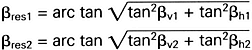
2. Shaft with three joints
In cases where greater distances between units have to be bridged, the
universal shaft must be supported by an additional, mostly elastic, bearing.
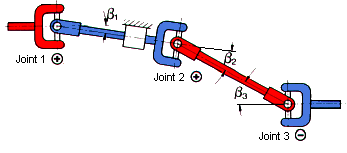
In order to keep the remaining irregularity in the drive (joint 3) as small as
possible, the sum of all irregulanties of the individualjoints must be equal to
or almost equal to zero.
![]()
(See 'Kinematics of Hooke's joints')
The signs must be entered according to the following sign rule. Here the sign
rule is:
![]() for
the joint position
for
the joint position
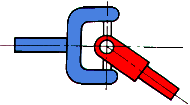
![]() for
the joint position
for
the joint position
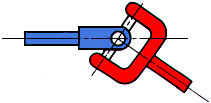
The remaining non-uniformity if any should not be greater than:
![]()
The minimization of the remaining non-uniformity can also be
achieved by the so-called equivalent deflection angle ![]() erfolgen.
erfolgen.
![]()
The sign rule is also applicable here.
The equivalent deflection angle ![]() =
3° is the equivalent deflection angle of a single joint which corresponds with
a degree of non-uniformity U = 0,0027.
=
3° is the equivalent deflection angle of a single joint which corresponds with
a degree of non-uniformity U = 0,0027.
3. Shafts with several joints
In case of an arrangement with more than three joints proceed as described
above.
General recommendations for lorry drives:
|
|
For fast-running drive shafts observe the instructions on
the transverse whirling speeds for installation length. |
|
|
Choose small resulting deflection angles for the main
drive range: |
|
|
Minimize the angular difference between the joints and the remaining inequaltity |
If these recommendations are not observed, one must reckon with vibrations and
noises and with a reduced driving comfort as well as with a reduced lifetime of
the units.
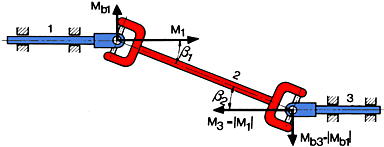
Deflection of joints in two planes
If a 'classic shaft arrangement' cannot be realized and the joint
deflection cannot be changed, this can be offset by turning the joints. For
this shaft arrangement the Installation rule that the resulting deflections of
the joints must be equal remains in force, i.e.
![]()
Plane 1 formed by the driving
shaft 1 and the connecting shaft 2 on the one hand and Plane II formed by the
connecting shaft 2 and the driven shaft 3 on the other hand form the angle ![]() which
is offset by turning the joints correspondingly.
which
is offset by turning the joints correspondingly.
The torsion angle ![]() is
determined as follows:
is
determined as follows:
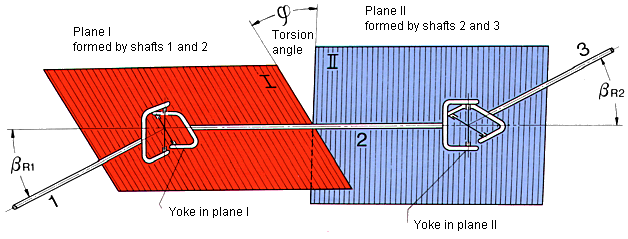
Yoke=furcǎ
The rotation direction results ifom the side view, i.e. joint 1 must be turned
to plane 1 by the angle ![]() .
.
The shaft must be mounted according to these statements and this before
a possible balancing. This position of the joints must be marked with arrows.
|
|
lnfluence of speed
and deflection angle
Speed
The permissible speed of the universal joint shaft is influenced by the
following parameters:
![]() size
of the shaft
size
of the shaft
![]() widening
of the yokes due to centrifugal force
widening
of the yokes due to centrifugal force
![]() quality
of balancing
quality
of balancing
![]() true
running of the connected flanges
true
running of the connected flanges
![]() deflection
angle during operation
deflection
angle during operation
![]() length
of the shaft
length
of the shaft
Speed x deflection angle
Theoretical considerations and observations of various applications have shown
that certain mass acceleration moments of the centre part of the shaft must not
be exceeded if a quiet running of the shaft drives is to be achieved. This mass
acceleration moment depends on the speed n, the deflection angle ß and the mass
moment of inertia of the centre part of the shaft.
The mechanically possible deflection angle for each joint depends on the size
of the shaft. Owing to the kinematic conditions of the universal joint
described before, the practical deflection angle must be limited in relation to
the rotational speed.
The following table shows the max. speeds and the max. permissible values for
the product
![]()
of the various shaft sizes for
a moment of inertia of the centre part according to a shaft length of approx.
1500 mm.
When approaching the critical rotational speed and in the light of the demand
of maintenance of balance quality (see Balancing
of Propeller shafts ) , it may be necessary to reduce the rotational speed.
Since the quiet running of the universal shaft in practice also largely depends
on the installation conditions, the n x ß values shown in the table can only be
regarded as a guidance. Slightly higher values are possible. In case of
favourable spring and mass conditions the values may be exceeded by up to 50 %.
Transverse whirling speed
Universal shafts are flexible elastic units, which must be calculated
considering the bending vibrations and the transverse whirling speed.
For reasons of safety the max. perm. operating speed must be sufficiently below
the transverse whirling speed.
The diagram on the end of this page shows the transverse whirling
speeds of the varbus shaft sizes depending on the operating lengths
and the tube dimensions shown in the catalogue.
The diagram values apply to normal installation conditions with a supposed
distance of the centre point of the joint shaft from the adjacent bearing equal
to 3 x M and a rigid suspension of the connected units.
In order to achieve a safe and quiet running behaviour the max. perm. operating
speed, i.e. including a possible excess speed, must not exceed 80 % of the
transverse whirling speed shown in the diagram.
![]()
If the permissible speed is
exceeded, the length of the universal shaft must be reduced or an intermediate
bearing must be provided.
The following diagrams only refer to universal shafts of the standard design.
For special designs with greater length compensations than normal or with other
alterations reducing the flexural strength a special calculation of the
critical speed is required. In this case please ask our advice.
Transverse whirling speed of cardan shafts dependent on operating
length ![]()
Load on connection
bearings
The bearings of the driving and the driven shafts are strained by statle and
dynamic forces and moments.
These bearing forces result from:
Static bad due to
![]() the
weight of the universal shaft
the
weight of the universal shaft
![]() the
length compensation under torque
the
length compensation under torque
![]() the
torque deviation in case of deflected universal shafts
the
torque deviation in case of deflected universal shafts
Dynamic bad due to
![]() the
remaining unbalance of the shafts
the
remaining unbalance of the shafts
![]() the
aperiodical length compensation (axle movement) under torque
the
aperiodical length compensation (axle movement) under torque
![]() the
torque deviation in case of rotating, deflected shafts and
the
torque deviation in case of rotating, deflected shafts and
![]() centrifugal
forces in case of untrue running of the connected units
centrifugal
forces in case of untrue running of the connected units
Bearing forces due to torque deviation
The torque equation for a deflected joint is:
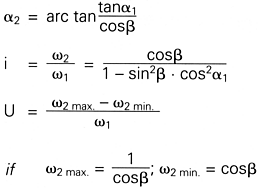
(See 'General fundamental theory ')
If the transmitted power (N) is taken as constant (no friction losses), the
torque relation can also be es follows:
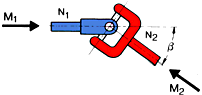
![]()
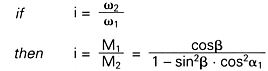
The extremes of the transmission i are:

Thus also:
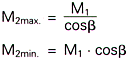
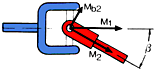
Bearing forces due to Iengh alteration


![]()
With a constant drive capacity resp. with a constant drive torque ![]() and
a constant angular drive velocity
and
a constant angular drive velocity ![]() an
irregular torque behaviour is obtained in the drive. Since the torque is only
transmitted in the journal cross plane, the cross, however, has a horizontal
position with regard to the drive shaft at one moment and a vertical position
with regard to the driven shaft at another moment, depending on the position of
the yoke, there is, in the former case, a bending torque
an
irregular torque behaviour is obtained in the drive. Since the torque is only
transmitted in the journal cross plane, the cross, however, has a horizontal
position with regard to the drive shaft at one moment and a vertical position
with regard to the driven shaft at another moment, depending on the position of
the yoke, there is, in the former case, a bending torque ![]() on
the yoke of the driven shaft and, in the latter case, a bending torque
on
the yoke of the driven shaft and, in the latter case, a bending torque ![]() on
the yoke of the driving shaft.
on
the yoke of the driving shaft.
Thus the driven torque ![]() fluctuates
twice per rotation between the extreme values
fluctuates
twice per rotation between the extreme values
![]() /
cos ß and
/
cos ß and ![]() *
cos ß
*
cos ß
![]() =
0°; 180°
=
0°; 180°

![]() =
90°; 270°
=
90°; 270°
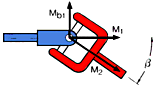
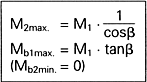
The universal shaft with two joints in the Z-arrangement shown is Ioaded with
the following moments. Here, as for the single joint, only the two extreme
positions are shown.
![]() =
90°; 270°
=
90°; 270°
![]() =
=
![]()
![]() =
0°; 180°
=
0°; 180°
![]() =
=
![]()
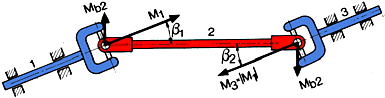

In general:
![]()
Radial forces on connecting bearings
For universal shafts with two joints mounted normally while observing the
installation instructions it is usually enough to know the greatest reaction
forces in the bearings of the driving and driven shafts, which occur two times
per rotation. The following calculation scheme may be helpful. (See 'Calculation
scheme')
Axial forces on connecting bearings
Axial forces on connecting bearings are encountered in the form of
reaction forces due to:
![]() displacement
of the engine / transmission and / or transfer box units
displacement
of the engine / transmission and / or transfer box units
![]() axle
displacements
axle
displacements
These axial forces are a function of:
![]() the
amounts of torque to be transmitted
the
amounts of torque to be transmitted
![]() the
sectional dimensions of Ion gitudinal compensating elements
the
sectional dimensions of Ion gitudinal compensating elements
![]() the
friction coefficient in Ion gitudinal compensating elements
the
friction coefficient in Ion gitudinal compensating elements
![]() the
deflection angles of the cardan shaft under operating conditions
the
deflection angles of the cardan shaft under operating conditions
![]() the
relative dynamic displacement of engine and transmission units
the
relative dynamic displacement of engine and transmission units
![]() additional
loads due to hydraulic effects arising when the grease
additional
loads due to hydraulic effects arising when the grease
![]() chamber
in the Ion gitudinal displacement system is filled beyond capacity
chamber
in the Ion gitudinal displacement system is filled beyond capacity
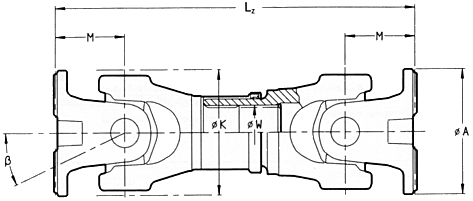
Calculation scheme of radial forces on connecting bearings
|
Universal shaft in Z-arrangement |
Universal shaft in
W-arrangement |
|
|
|
Length dimesions
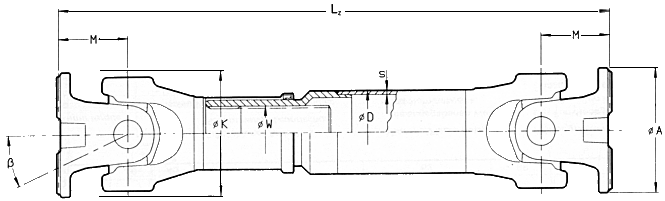
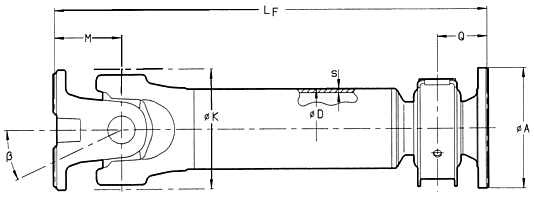
The operating length of a universal shaft is determined by:
![]() the
distance between the driving and the driven units
the
distance between the driving and the driven units
![]() the
length compensation during operation
the
length compensation during operation
The following abbreviations are used:
Lz = Compressed length
This is the shortest length of the shaft. A further compression is not
possible.
La = Length compensation
The universal shaft can be expanded by this factor La is a constant factor for
each universal shaft. An expansion beyond that factor is not permissible.
Lz + La = Max. perm. operating length LBmax.
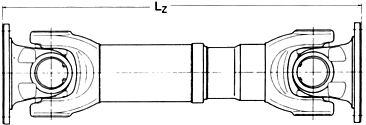
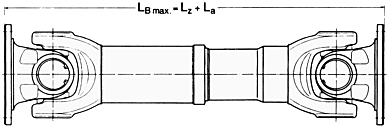
During operation the universal shaft can be expanded up to this length. The
optimum working length LB of a universal
shaft is achieved if the length compensation is extracted by one-third of its
length.
![]()
This rough rule appiles to most of the arrangements. For
applications where larger length alterations are expected the operating Iength
should be chosen in such a way that the movement will be within the limit of
the permissible length compensation.
Arrangements of cardan shafts
A tandem arrangement of universal shafts could become necessary
![]() to
cope with greater installation lengths
to
cope with greater installation lengths
![]() to
by-pass construction units
to
by-pass construction units
Basic forms of shaft combinations:
Universal shaft with intermediate shaft
![]()
Universal shaft with two intermediate shafts
![]()
2 universal shafts with double intermediate bearing
![]()
Copyright © 2025 - Toate drepturile rezervate