Reglarea robusta = reglarea sistemelor incerte

1)Problema stabilizarii robuste si reglarii

Reglarea robusta = reglarea sistemelor incerte (cu incertitudini) cu ajutorul unor regulatoare fixate.

Modelarea unui sistem fizic in vederea reglarii prin reactie implica un compromis intre simplitatea modelului si precizia cu care acesta exprima comportarea sistemului fizic.

Un regulator robust, pe langa satisfacerea cerintei minime de stabilizare a modelului nominal al sistemului, stabilizeaza o clasa de sisteme care sunt apropiate de instalatia nominala.

Daca un sistem este stabilizabil, exista un intreg set de compensatoare stabilizatoare. Trebuie ales compensatorul care stabilizeaza cea mai larga clasa de sisteme si care satisface o serie de criterii de performanta.

Proiectarea compensatorului robust se face ca un compromis intre cerintele de stabilizare robusta si performanta robusta.

Problema reglarii robuste: Fiind data o instalatie nominala si limitele perturbatiilor, sa se determine un compensator fixat care conduce la un sistem in circuit inchis cu performante satisfacatoare pentru toate instalatiile si semnalele perturbatoare admisibile.

O problema importanta este selectarea punctelor nominale de functionare si a limitelor incertitudinilor pentru probleme fizice particulare.

Modelul matematic trebuie sa contina informatii despre comportarea dinamica si despre perturbatii. Daca modelul dinamic este exact, iar perturbatiile reprezinta zgomote Gaussiene, atunci se foloseste proiectarea LGP (Liniar - Gaussian - Patratica).

O norma corespunzatoare care poate incorpora atat amplificarea semnalelor cat si robustetea la incertitudinile instalatiei este norma .Se proiecteaza un regulator care sa optimizeze performantele sistemului in circuit inchis pentru marimile exogene cele mai defavorabile.

2)Modelarea incertitudinilor

Diferentele intre instalatia reala si modelul nominal se numesc erori de modelare sau incertitudinea sistemului.

Cauzele de aparitie ale acestor erori pot fi:

-utilizarea unui model liniar, daca majoritatea sistemelor sunt neliniare

-includerea in modelul nominal doar a modurilor dominante

-dinamica nemodelata, dinamica parazita la frecvente inalte

-determinarea imprecisa a parametrilor modelului

-tolerantele componentelor

-abaterile datorate imbatranirii componentelor

-modificarile comportarii sistemului real datorate unor factori externi perturbatori

Modelarea incertitudinilor se poate realiza:

in domeniul timp

in domeniul frecventa

a)Modelarea in domeniul timp

Spatiul starilor: G A,B,C,D)

Functia de transfer reala: G_Δ A+ΔA,B+ΔB,C+ΔC,D+ΔD)

Presupunem A=stabila si notam || ΔA||=ρ raza de stabilitate este instabila}

Aceasta forma de modelare, in care incertitudinile matriceale pot fi variabile in timp, este abordata de mai multi autori in conexiune cu problema stabilizarii patratice.

b)Modelarea in domeniul frecventa

Incertitudinea se presupune a fi complexa si dependenta de frecventa. Incertitudinea nestructurata este incertitudinea despre care nu este disponibila nici o informatie privind efectele acesteia asupra unui proces, cu exceptia unei limite superioare a marimii sale, ca o functie de frecventa, care poate fi estimata. Aceste incertitudini au ca efect modificarea ordinului sistemului nominal fata de cel real si sunt caracterizate cantitativ prin normele functiilor de transfer sau ale operatorilor prin care se descriu incertitudinile respective.

Incertitudinea structurata este incertitudinea despre care este disponibila o informatie "structurala", ceea ce conduce la restrangerea incertitudinii la o portiune a modelului procesului. Este de dorit sa se "structureze" incertitudinea, intrucat aceasta restrange clasa de incertitudini pentru care trebuie sa fie proiectat regulatorul.

Cele mai utilizate moduri de reprezentare a incertitudinilor in domeniul frecventa sunt: aditiv, multiplicativ si de tip numarator - numitor (utilizand descompunerea in factori coprimi).

Fie G si G_Δ matricele (functiile) de transfer ale modelului nominal si, respectiv, perturbat (real) al instalatiei.

O incertitudine Δ_A se numeste incertitudine aditiva daca G_Δ=G+ Δ_A

O incertitudine Δ_P se numeste incertitudine multiplicativa (proportionala) daca G_Δ I+ Δ_P)G (*)

O incertitudine [Δ_N,Δ_M] se numeste incertitudine in factori coprimi daca, unde reprezinta o factorizare coprima la stanga a lui G, , iar si reprezinta o factorizare coprima la stanga a lui G_Δ.

Relatia (*) defineste o incertitudine multiplicativa la iesire. Uneori se utilizeaza reprezentarea incertitudinii multiplicative la intrare: G_Δ=G(I+Δ_i) sau combinat G_Δ=(I+Δ_P)G(I+Δ_i).

Singura informatie disponibila despre perturbatie este o limita dependenta de frecventa asupra marimii acesteia. O masura corespunzatoare a marimii unei matrici de transfer este valoarea singulara maxima, notata .

In reprezentarea c), factorii lui G si G_Δ pot fi alesi arbitrar cu conditia ca si sa fie coprime. Intrucat, prin definitie, sunt stabile, perturbatiile Δ_N si Δ_M vor fi intotdeauna stabile.

Fig.3.2.1 Reprezentarea incertitudinilor (Pag.32)

3)Transformari liniar-fractionare

Se numeste transformata liniar-fractionara (TLFI) matricea de transfer de la w la z (fig.3.2.2.a) si se noteaza: 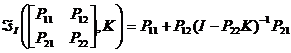daca det(I-P₂₂K)≠0

Se numeste transformata liniar-fractionara superioara (TLFS) matricea de transfer de la w la z (fig.3.2.2.b) si se noteaza: 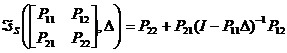daca det(I-P₁₁Δ)≠0

TLFI se utilizeaza in formularea multor probleme de conducere H_∞, iar TLFS ofera un mijloc foarte general pentru descrierea sistemelor incerte.

Sistemul din fig.3.2.2.a se numeste bine-definit daca TLFI este proprie.

Daca matricea (I-P₂₂K ∞) este inversabila, atunci sistemul din fig.3.2.2.a este bine-definit.

Pentru fiecare din cele 3 clase de incertitudini, modelul sistemului perturbat, G_Δ, poate fi reprezentat in forma unei "transformari liniar-fractionare superioare" (TLFS) indicata in fig.3.2.3.

Fig.3.2.2. Transformari liniar-fractionare (Pag.33)

Fig.3.2.3. Modelul generalizat al incertitudinii (Pag.34)

P=instalatia standard continand instalatia nominala (G) si conexiunile, Δ=modelul incertitudinii corespunzatoare.

Instalatiile standard asociate cu cele 3 descrieri ale incertitudinii sunt:

a)Incertitudine aditiva: , (Δ=Δ_A)

b)Incertitudine multiplicativa (la iesire): , (Δ=Δ_P)

c)Incertitudine in factori coprimi (la stanga): 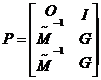, (Δ=[Δ_N,- Δ_M])

Fig.3.2.4. Instalatiile standard (Pag.35)

4)Stabilitatea robusta

Un compensator stabilizeaza robust un proces daca acesta stabilizeaza orice model perturbat G_Δ (descris prin una din configuratiile din fig.3.2.1), care reprezinta o combinatie a modelului nominal G si modelului incertitudinii ΔєD_ε, unde D_ε este o clasa de incertitudini posibile care include Δ=0.

Scriind modelul sistemului perturbat G_Δ, sub forma unei TLFS , modelul nominal poate fi scris astfel: .

O perturbatie permisibila (admisibila), Δ, este o perturbatie care apartine unui domeniu admisibil, ΔєD_ε, unde si D_Sε= si P q ale familiei initiale de polinoame .

Pentru subfamilia P q se defineste marginea de robustete la dreapta q_max⁺ sup iar pentru subfamilia P q se defineste marginea de robustete la stanga

q_min^- inf

In continuare, vom numi Q_max q_min^-,q_max⁺) intervalul maxim de stabilitate robusta.

Matricea Hurwitz asociata unui polinom fixat, p s a_nsⁿ a_n-1s^n-1 a₁s a₀ , a_n>0 este:

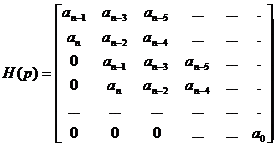
Definitie Fiind data o matrice n n, M, se defineste λ_max⁺(M) ca fiind valoarea proprie reala pozitiva maxima a lui M. Cand M nu are nici o valoare proprie reala pozitiva, se ia λ_max⁺(M)=0⁺ . Similar, se defineste λ_min^-(M) ca fiind valoarea proprie reala negativa minima a lui M. Cand M nu are valori proprii reale negative, se ia λ_min^-(M)=0^- .

Criteriul valorii proprii: Se considera polinomul incert p s, q p₀ s qp₁ s cu p s p₀ s stabil si avand coeficienti pozitivi si grad p₀ s)>grad p₁ s . Atunci, intervalul maxim pentru stabilitate robusta este descris prin: si

unde, pentru compatibilitatea inmultirii matricelor, H p₁ este o n n-matrice obtinuta prin tratarea lui p₁(s) ca un polinom de ordin n.

Demonstratia acestei teoreme se bazeaza pe urmatoarele doua leme:

Lema 1 Se considera familia de polinoame P descrisa prin si .Se presupune ca P are grad invariant si functiile coeficientilor a₀ q ,a₁ q ,a₂ q , ,a_n q depind continuu de q. Atunci radacinile lui p s, q variaza continuu in raport cu . Adica, exista transformarile continue s_i : Q C pentru i 1,2, ,n astfel incat s₁ q ,s₂ q , ,s_n q sunt radacinile lui p s, q .

Lema 2 Se considera familia de polinoame P descrisa prin p s, q p₀ s qp₁ s si domeniul incertitudinii Q q ,q . Se presupune ca p₀ s are coeficienti pozitivi, este stabil si grad p₀ s)>grad p₁ s). Atunci, subfamilia P q este stabila robust H p , q este nesingulara oricare ar fi . Similar, subfamilia P q este stabila robust H p , q este nesingulara oricare ar fi .

Demonstratia criteriului: Vom demonstra doar formula pentru q_max⁺ obtinerea lui q_min^- urmand o cale similara.

Pentru q 0 fixat, din Lema 2 rezulta ca P q⁺ este stabila robust H p , q este nesingulara oricare ar fi . Deoarece H p , q H p₀ qp₁ H p₀ qH p₁ rezulta ca q_max⁺ este cea mai mare valoare a lui q⁺ astfel incat det H p₀ qH p₁ 0, . Intrucat p₀ este stabil, H(p₀) este inversabila si multiplicand prin H^-1(p₀)/q se obtine caracterizarea lui q_max⁺ prin conditia .

Se considera urmatoarele doua cazuri:

a) Matricea H^-1 p₀ H p₁ nu are nici o valoare proprie reala pozitiva. In acest caz nu exista nici o valoare q > 0 conducand la anularea determinantului. Deci, se obtine q_max⁺

b) Matricea H^-1 p₀ H p₁ are valorile proprii reale pozitive 0 < λ₁⁺ ₂⁺ _k . Deci, cea mai mare valoare a lui q>0 conducand la o neanulare a determinantului este q_max⁺=1/λ_k⁺.

Combinand aceste doua cazuri se obtine .

Observatie: Se considera p s,q p₀ s qp₁ s cu Q q , q ]. Familia de polinoame asociata are punctele extreme p s, q si p s, q . Se exprima p s, q ca o combinatie convexa de punctele extreme, considerand: si scriind .

Invers, pentru orice exista un astfel incat . Fiind dat acest izomorfism intre si , este indiferent daca se lucreaza cu familia initiala de polinoame sau cu o familie echivalenta definita prin: , unde si sunt polinoame fixate. Adica .

Daca notam f s p₀ s q^-p₁ s si g s q q^- p₁ s si definim p s, f s g s familia de polinoame coincide cu familia initiala. Pentru a demonstra acest lucru se alege .

Notiunea de stabilitate robusta poate fi extinsa la un domeniu D mai general pentru plasarea polilor. In acest fel se poate obtine o teorie unificata care se aplica atat sistemelor continue cat si celor discrete in timp. In cazul continuu, este convenabil sa se aleaga D ca o submultime a semiplanului stang, iar in cazul discret D este aleasa ca o submultime a discului unitate.

Definitie: Fie si p s un polinom fixat. Atunci, se spune ca p s este D-stabil daca toate radacinile acestuia se afla in domeniul D.

Definitie: O familie de polinoame se spune ca este D-stabila robust daca, pentru orice , p s, q este D-stabil; adica toate radacinile lui p s, q se afla in D.

Observatie: Metoda locului radacinilor poate fi utilizata pentru testarea proprietatii de stabilitate D-robusta.

12)Criteriul Routh-Kurwitz

Se considera polinomul: p s a₀sⁿ a₁s^n-1 a_n-1s a_n cu coeficienti reali a₀,a₁, ,a_n. Cu ajutorul acestor coeficienti se formeaza tabloul Routh (acesta contine n+1 linii si n /2 coloane, unde 1 daca n este impar si 2 daca n este par).

Primele doua linii se formeaza direct cu coeficientii de ordin par si, respectiv, impar ai polinomului p s . In continuare, elementele din tablou se calculeaza ca un raport intre un determinant de ordinul 2 (format din elementele de pe cele doua linii precedente liniei curente, coloana 1 si, respectiv, coloana urmatoare coloanei curente) si elementul de pe coloana 1, linia precedenta. Astfel, elementele r_ij se calculeaza succesiv cu relatiile:

,

,

.

,

.

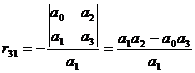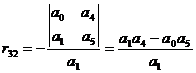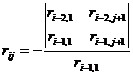Tabloul lui Routh (pag.64)

Conditia necesara si suficienta pentru ca polinomul p s sa fie strict Hurwitz (sa aiba toate radacinile in semiplanul stang deschis) este ca toate elementele de pe prima coloana a tabloului sa fie nenule si sa aiba acelasi semn.

Observatie: O conditie necesara de stabilitate este ca toti coeficientii polinomului p s , a₀, a₁ a_n sa fie nenuli si sa aiba acelasi semn.

In principiu, criteriul Routh-Hurwitz permite stabilirea domeniului de stabilitate al polinomului p s dependent de vectorul parametru q, adica multimea tuturor valorilor parametrilor pentru care radacinile lui p s au partea reala strict negativa.

13)Stabilitatea in planul parametrilor

Studiul stabilitatii in planul parametrilor se poate realiza pornind fie de la polinomul caracteristic al sistemului in circuit inchis, fie de la functia de transfer a sistemului in circuit deschis. Aceasta metoda permite determinarea pe cale grafica a domeniilor de forma D(n-r, r) din planul parametrilor, unde n reprezinta ordinul sistemului, iar r numarul de radacini din semiplanul drept al planului complex. Evident, ne intereseaza domeniile de stabilitate, D(n, 0). Trecerea peste frontiera domeniilor corespunde trecerii radacinilor polinomului caracteristic peste axa imaginara. Deci, frontierele domeniilor corespund imaginii axei imaginare prin polinomul caracteristic.

Problema unidimensionala liniara

Se considera ca vectorul parametru q contine un singur parametru, , si acesta intervine liniar in polinomul caracteristic al sistemului in circuit inchis p s . Atunci, din:

p , j U j V j 0 →

Se reprezinta in planul P_λ ,Q_λ , parametrizat dupa . Se hasureaza graficele pe partea stanga in sensul cresterii lui de la la .

Observatie: Portiunea cu hasura corespunde unui numar mai mic de radacini in semiplanul drept (r mai mic).

Printr-un criteriu cunoscut (de exemplu, Routh-Hurwitz) se stabileste valoarea lui r intr-un anumit domeniu. Din domeniul D(n, 0) se retin doar valorile reale ale parametrului .

Problema bidimensionala liniara

Se considera polinomul caracteristic de forma p , , s U s V s W s .

Din p , , j 0, rezulta sistemul: 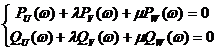cu solutiile si . Se traseaza aceste curbe in planul , si se completeaza cu o serie de drepte singulare:

a) corespunzatoare anularii coeficientului puterii maxime a lui s (α_n(λ, 0 ; aceasta corespunde trecerii unei radacini simple pe la infinit dintr-un semiplan in celalalt.

b) corespunzatoare anularii termenului liber , 0 ; aceasta corespunde trecerii prin origine a unei radacini simple dintr-un semiplan in celalalt.

Utilizand un criteriu cunoscut (Routh-Hurwitz) se determina domeniul de stabilitate D(n, 0).

Metoda 'grilei'

Aceasta metoda consta in acoperirea partii relevante din spatiul parametrilor cu o retea (grila), si testarea stabilitatii in fiecare nod al retelei. Nu este obligatoriu ca reteaua sa fie rectangulara. Evident, acest lucru se poate realiza usor cu ajutorul calculatorului. Totusi, numarul nodurilor retelei creste exponential cu dimensiunea spatiului parametrilor si sarcina de calcul pentru o retea suficient de fina poate deveni enorma.

Exemplu: Pentru polinomul se considera domeniul din planul parametrilor (T, g) definit prin 0, 05 T 1, 4 si 0, 5 g 7, 5. Se alege o retea rectangulara cu pasul 0,15 pe axa T si 1 pe axa g. Reteaua va contine 10 8 80 puncte in care trebuie testata stabilitatea (utilizand, spre exemplu, criteriul Routh-Hurwitz). Domeniul de stabilitate care se obtine este reprezentat in figura, unde semnul minus corespunde punctelor de stabilitate iar semnul plus punctelor de instabilitate.

Fig. 4.4.1. Domeniul de stabilitate (metoda grilei - pag.68)

14)Incertitudini cu structuri independente. Familii de polinoame pe interval

Incertitudini cu structuri independente

Incertitudinile cu structuri independente, pot fi tratate cu o teorie relativ simpla care permite apoi trecerea la incertitudini cu structuri mai complexe.

Studiul incertitudinilor cu structuri independente este motivat si de urmatoarele doua argumente:

a) Se presupune ca pentru un sistem de reglare se determina polinomul caracteristic asociat p s . Desi se cunoaste existenta incertitudinii parametrice, dependenta coeficientilor de q este complicata si puternic neliniara ceea ce nu permite o analiza matematica. Totusi, sunt necesare anumite informatii despre gradul de robustete. Presupunand o incertitudine cu structura independenta, se

poate determina variatia procentuala a coeficientilor polinomului p s care poate fi tolerata.

b) In anumite situatii, o structura mai complicata a incertitudinii poate fi acoperita printr-o structura independenta a incertitudinii. Astfel, din rezultatele obtinute pentru cazul independent se deduc, adesea, conditii suficiente pentru cazul mai complicat considerat.

Definitie: Un polinom incert se spune ca are o structura independena a incertitudinii daca fiecare componenta q_i a lui q intervine numai intr-un singur coeficient.

Familii de polinoame pe interval

Definitie: O familie de polinoame se spune ca este o familie de polinoame pe interval daca p s, q are o structura independenta a incertitudinii, fiecare coeficient depinde continuu de q si Q este o 'cutie'.

Observatie: Ne vom referi la P ca la un polinom pe interval.

Teorema: Se considera o familie de polinoame pe interval avand coeficientii depinzand continuu de q. Atunci, exista o a doua familie de polinoame pe interval cu de forma si, in plus .

Tinand cont de aceasta teorema, in continuare se va utiliza un polinom de forma cand se lucreaza cu o familie de polinoame pe interval. O descriere completa a

familiei, intr-o forma prescurtata, este , unde [q_i^-,q_i⁺] defineste intervalul de marginire pentru componenta q_i a incertitudinii.

15)Polinoame Haritonov. Teorema lui Haritonov (aplicatie)

Definitie: Pentru un polinom pe interval se asociaza urmatoarele patru polinoame Haritonov fixate:

K₁(s q₀^-+q₁^-s+q₂⁺s²+q₃⁺s³+q₄^-s⁴+q₅^-s⁵+q₆⁺s⁶+.

K₂(s q₀⁺+q₁⁺s+q₂^-s²+q₃^-s³+q₄⁺s⁴+q₅⁺s⁵+q₆^-s⁶+.

K₃(s q₀⁺+q₁^-s+q₂^-s²+q₃⁺s³+q₄⁺s⁴+q₅^-s⁵+q₆^-s⁶+.

K₄(s q₀^-+q₁⁺s+q₂⁺s²+q₃^-s³+q₄^-s⁴+q₅⁺s⁵+q₆⁺s⁶+.

Teorema Haritonov: O familie de polinoame pe interval P cu grad invariant este robust stabila ↔ cele patru polinoame Haritonov ale sale sunt stabile.

Observatie: Polinoamele Haritonov sunt fixate in sensul ca in acestea intervin doar limitele q_i^- si q_i De asemenea, numarul de polinoame este patru indiferent de gradul lui p s, q .

Dreptunghiul Haritonov

Se considera un polinom pe interval si se urmareste descrierea multimii tuturor valorilor posibile ale lui p j , q cand (Q - o 'cutie'), iar frecventa ₀ este fixata, adica . p j ,Q se numeste dreptunghiul lui Haritonov la frecventa . In continuare, se va demonstra ca p j ,Q este un dreptunghi cu varfurile K_i j , unde K_i, i 1, 4 reprezinta polinoamele Haritonov.

Se observa ca

adica Rep j , q si Imp j , q sunt decuplate din punct de vedere al incertitudinilor care intervin in acestea.

Intrucat fiecare componenta q_i intervine doar intr-un singur coeficient al lui p s, q , determinarea valorilor minime si maxime ale lui Rep j , q , se poate realiza prin minimizarea sau maximizarea fiecarui termen, obtinand:

Pentru minimizarea si maximizarea lui Imp j , q trebuie sa se tina cont de semnul lui ₀ . Astfel, pentru ₀ 0 obinem

iar pentru ₀ < 0 :

Combinand aceste doua cazuri se obtine:

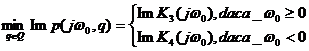
Similar, se obtine:

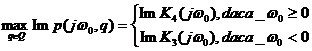
Astfel, p j ,Q este marginit de dreptunghiul din figura, pentru ₀ 0.

Fig. 5.1.1. Dreptunghiul Haritonov pentru 0 0 (pag.73)

Fiecare varf al dreptunghiului Haritonov poate fi asociat unui singur polinom Haritonov, astfel:

A ReK₁ j jImK₃ j ReK₁ j jImK₁ j K₁ j

B ReK₂ j jIm K₃ j Re K₃ j jIm K₃ j K₃ j

C Re K₂ j jImK₄ j Re K₂ j jIm K₂ j K₂ j

D Re K₁ j jIm K₄ j Re K₄ j jIm K₄ j K₄ j

Descrierea finala a dreptunghiului Haritonov este reprezentata in figura 5.1.2.

Observatie: In mod asemanator se trateaza cazul ₀ < 0. Pentru ₀ 0 se obtine p j ,Q q₀^-,q₀⁺

Daca pulsatia se creste incepand de la valoarea 0 se obtine o miscare a dreptunghiului in planul complex, varfurile acestuia fiind K_i j , i 1, 4. In general, dimensiunile acestui dreptunghi variaza cu frecventa (el incepe la 0 ca un interval pe axa reala).

Fig. 5.1.2. Dreptunghiul Haritonov simplificat, pentru 0 0 (pag.74)

Proprietatea de monotonie a unghiului: Se presupune ca p s este un polinom stabil. Atunci, unghiul (argumentul) lui p j este o functie strict crescatoare de . In plus, cand variaza de la 0 la , argumentul lui p j sufera o crestere de n /2 radiani.

Observatie: Daca p s este un polinom de gradul n cu n1 radacini in semiplanul stang deschis si n2 radacini in semiplanul drept deschis si n1 n2 n, atunci cand variaza de la 0 la argumentul lui p j sufera o schimbare totala de n1 n2 /2 radiani.

Conditia de excludere a originii: Presupunem ca o familie de polinoame pe interval are grad invariant si cel putin un element stabil p s, q⁰ Atunci, P este stabila robust ↔ z = 0 este exclus din dreptunghiul Haritonov la toate frecventele nenegative, adica,

Restrictia la frecvente 0 provine din observatia ca .

Exemplu: Reluam analiza sistemului cu polinomul caracteristic (1). Presupunem ca variatiile parametrilor instalatiei sunt cunoscute intre limitele , 0 T ≤ (2). Atunci, coeficientii polinomului se aflá íntre limitele , , , , (3).

Presupunem 0, 2, iar pentru g consideram doua cazuri:

1. 0 si 5. In acest caz cele patru polinoame Haritonov sunt:

K₁ s 0, 5 0, 5s s² 0, 3 s³

K₂ s 5 5s s² 0, 1 s³ 0, 02 s⁴

K₃ s 5 0, 5s s² 0 s³ 0, 02 s⁴

K₄ s 0, 5 5s s² 0, 1 s³

Utilizand criteriul Routh-Hurwitz sau calculand numeric radacinile rezulta ca polinoamele K₁ si K₄ sunt strict Hurwitz, pe cand K₂ si K₃ nu sunt polinoame Hurwitz. Aceasta arata ca polinomul

p s _{0 1} s ₂ s² ₃ s³ ₄ s⁴ nu este strict Hurwitz pentru toate variatiile coeficientilor intre limitele (3). Aceasta nu demonstreaza, totusi, ca sistemul in circuit inchis cu polinomul

caracteristic (1) nu este stabil pentru toate variatiile lui g si T intre limitele (3), intrucat coeficientii _i ai polinomului nu variaza independent in cadrul limitelor (2). De altfel, din figura 4.3.1 se observa ca domeniul de variatie considerat in acest exemplu pentru g si T se afla in domeniul de stabilitate.

2. 0 si 2 . Repetand calculele se gaseste ca, in acest caz, fiecare din cele patru polinoame Haritonov este strict Hurwitz astfel incat sistemul in circuit inchis este stabil pentru toate valorile parametrilor din domeniul considerat.

16)Margini de robustete. Testarea grafica a stabilitatii robuste

Se considera o familie de polinoame pe interval de ordinul n cu polinomul nominal p₀(s) stabil si limita incertitudinii variabila , r 0 descrisa prin . Aici, _i 0 reprezinta un factor de scalare care determina aspectul multimii de variatie a incertitudinii Q. Notand cu P_r familia de polinoame rezultata se pune problema determinarii unei formule pentru marginea de robustete r_max sup .

Problema marginii de robustete se poate reduce (pe baza Teoremei Haritonov) la patru probleme separate pentru polinoamele incerte _i=1⁴ , unde

P₁ s ₀ s s² s³ s⁴ s⁵ s⁶

P₁ s ₀ s s² s³ s⁴ s⁵ s⁶

P₁ (s) ₀ s s² s³ s⁴ s⁵ s⁶

P₁ s ₀ s s² s³ s⁴ s⁵ s⁶

Apoi, aplicand criteriul valorii proprii si considerand cazul cel mai defavorabil in raport cu i 1, 4, se obtine formula .

Testarea grafica a stabilitatii robuste

Conditia de excludere a originii sugereaza o procedura grafica simpla pentru verificarea stabilitatii robuste si anume urmarirea miscarii dreptunghiului Haritonov p j ,Q cand variaza de la 0 la (se urmareste satisfacerea conditiei 0 p j ,Q ).

In realitate conditia nu se testeaza decat pe un interval finit de frecvente ω [0, ω_c]. Existenta lui _c astfel incat 0 p j ,Q , _c este asigurata de conditia de rang invariant. Intr-adevar, presupunand (fara pierderea generalitatii) q_i^-> i 0, n , se poate arata ca: . Intrucat membrul drept tinde la cand rezulta ca oricare ar fi β > 0 exista un _c > 0 astfel incat |p j , q oricare ar fi ω > ω_c. Deci,

0 p j ,Q , ω > ω_c . Se poate alege _c , spre exemplu, ca fiind cea mai mare radacina reala a polinomului .

17)Instalatii pe interval cu reactie unitara

Definitie: O familie de instalatii pe interval P este descrisa prin cu un polinom numarator incert , polinom numitor incert si cutiile Q si R ca multimi limita ale incertitudinii pentru q si, respectiv, r; adica, P este un raport de familii de polinoame pe interval. Pentru simplitate se scrie .

Se utilizeaza notatia P si, adesea, este denumita instalatie pe interval.

Pentru o instalatie pe interval proprie definita prin conditia n m, daca se utilizeaza reactia unitara, incertitudinile din polinomul in circuit inchis pot fi comprimate; adica . Deci, reactia unitara conserva structura polinomului pe interval.

Teorema Barmish Fie P o familie de polinoame pe interval cu grad invariant, cel putin un element stabil si polinoamele Haritonov asociate K₁ s , K₂ s , K₃ s si K₄(s Atunci, P este stabila robust ↔ H ω) > 0, 0 , unde H max .

Demonstratia acestei teoreme se bazeaza pe dreptunghiul Haritonov si conditia de excludere a originii.

Observatie: Pentru o familie de polinoame pe interval cu grad invariant, are loc relatia . Aceasta permite limitarea domeniului de frecventa la un interval 0, _c .

Considerand norma max clasica definita pentru numere complexe z C prin

||z|| max se poate demonstra, in ipotezele teoremei, ca daca 0 p j ,Q pentru

anumite frecvente 0, atunci . Deci, la o frecventa data 0, H reprezinta distanta in norma max de la origine la cel mai apropiat punct (in norma max) al dreptunghiului Haritonov p j ,Q .

Observatie: Pastrarea unei distante mari intre dreptunghiurile Haritonov p j ,Q , 0 , si origine (z = 0) nu semnifica existenta unei margini de robustete bune.

18)Incertitudini cu structuri liniar-afine

Definitie: Un polinom incert se spune ca are o structura a incertitudinii liniar afina daca fiecare coeficient a_i q este o functie liniar afina de q; adica, pentru fiecare i , exista un vector coloana _i si un scalar _i astfel incat a_i q) = α_i^Tq _i, unde α_i^T este transpusul lui _i. In general, o functie rationala incerta, care se scrie sub forma P s,q M s,q /N s,q , se spune ca are o structura a incertitudinii liniar afina daca ambele polinoame M s,q si N s, q au structuri ale incertitudinii liniar afine.

Se considera o instalatie incerta P s, q M s, q /N s, q conectata intr-o structura cu reactie ca in fig. 5.4.1 cu un compensator .

Functia de transfer in circuit inchis este

Fig. 5.4.1. Conexiunea cu reactie conservá structura incertitudinii (pag.86)

Lema: Se considera o instalatie incerta conectata intr-o configuratie cu reactie ca in fig. 5.4.1 si se presupune ca P s, q are o structura a incertitudinii liniar afina. Atunci, functia de transfer in circuit inchis incerta H_v s, q are, de asemenea, o structura a incertitudinii liniar afina.

Demonstratie. Considerand q R^l , structura liniar afina a incertitudinii permite exprimarea numaratorului si numitorului lui P s, q sub forma: si , unde M_i(s) si N_i(s) sunt polinoame fixate, i .

Numaratorul si numitorul functiei de transfer in circuit inchis sunt

Se observa ca M_v s, q si N_v s, q au, de asemenea, structuri liniar afine ale incertitudinii.

Observatie: Daca P s, q are o structura liniar afina a incertitudinii, atunci functia de sensibilitate si functia de sensibilitate complementara au, de asemenea, structuri liniar afine ale incertitudinii.

19)Teorema muchiei

Teorema muchiei stabileste ca pentru a verifica daca fiecare polinom din politop este Hurwitz, este suficient sa se verifice daca polinoamele de pe fiecare din muchiile expuse ale politopului sunt Hurwitz. Muchiile expuse se obtin fixand N-1 din parametrii q_i la valorile lor minime sau maxime si modificand parametrul ramas pe intervalul sau.

Teorema muchiei: Se presupune ca D este un subspatiu deschis simplu conex al planului complex si P este un politop de polinoame cu grad invariant. Atunci, P este D-stabil robust ↔ pentru fiecare pereche de puncte extreme qⁱ¹ si qⁱ² corespunzatoare unei muchii a

lui Q, polinomul p_i1,i2 s, p s, qⁱ¹ 1 p s, qⁱ² este D-stabil, [0, 1 .

Deci, toate radacinile fiecarui polinom din politop sunt continute in D ↔ radacinile fiecarui polinom de pe muchiile expuse ale politopului sunt continute in D.

Observatie: Un domeniu simplu conex este un domeniu pentru care fiecare contur inchis simplu (adica, un contur care nu se autointersecteaza) in interiorul domeniului inconjoara doar puncte din domeniu.

O alta posibilitate pentru testarea unei muchii implica generarea setului de valori.

Cu p_i1,i2 s, p s, qⁱ¹ 1 p s, qⁱ² si =[0, 1 , reamintim ca setul de valori p z, este un segment de dreapta cu capetele p z, 0 si p z, 1 . Deci, pentru fiecare muchie de acest tip, se verifica D-stabilitatea intr-unul din capete si apoi se verifica satisfacerea conditiei de excludere a originii 0 p z, pentru orice z ∂D ( D - reprezinta frontiera lui D).

Exemplu pag.91-92

20)Parametrizarea regulatorului (cazul instabil)

Se presupune functia de transfer a instalatiei, G, stabila. In cazul monovariabil, RH reprezinta multimea functiilor de transfer rationale, proprii si stabile.

Fig.6.1.1. Sistem cu reactie unitara (pag.102)

Se scriu relatiile intre marimile de intrare (r si d) si iesirile din sumatoare (e si v) pentru fig. . In forma matriceala acestea sunt: (1).

Sistemul este bine-definit ↔ matricea 2 2 din relatia (1) este nesingulara, adica determinantul 1 + GC nu este identic nul. Atunci, cele patru functii de transfer se obtin din ecuatia: adica (2)

Observatie: O conditie necesara si suficienta este ca 1 + GC sa nu fie strict proprie (adica,

GC 1).

Daca cele 4 functii de transfer din (2) sunt stabile, atunci sistemul cu reactie se numeste intern stabil.

Observatie: Stabilitatea interna garanteaza semnale interne marginite pentru orice semnale externe marginite.

Teorema 1: Presupunem ca G RH Multimea tuturor regulatoarelor C pentru care sistemul cu reactie din fig. 6.1.1 este intern stabil, este egala cu .

Demonstratie: (). Presupunem ca C asigura stabilitatea interna. Fie Q functia de transfer de la r la u, adica . Atunci, Q RH si .

(). Presupunem ca Q RH si definim (3).

Sistemul este intern stabil daca cele patru functii de transfer din (2), adica sunt stabile si proprii. Inlocuind pe C din (3) obtinem .

Se observa ca cele patru functii de transfer sunt functii afine de parametrul Q; adica, fiecare este de forma T₁ T₂Q pentru anumite functii T₁ si T₂ din RH . In particular, functiile de sensibilitate si sensibilitate complementara sunt: S=1-GQ si T=GQ.

Teorema 2: Presupunem ca sistemul cu reactie este intern stabil si d = 0.

a) Daca r este un semnal treapta, atunci e t 0 cand t S are cel putin un zerou in origine.

b) Daca r este un semnal rampa, atunci e t 0 cand t S are cel putin doua zerouri in origine.

Demonstratie: a) Pentru o intrare treapta, tinand cont ca functia de transfer de la r la e este S, obtinem . Intrucat S este o functie de transfer stabila, se aplica teorema valorii finale obtinand e S 0 k . Deci, e 0 S 0 0.

b) Se demonstreaza similar, considerand o intrare rampa k/s² .

Observatie: Se observa ca S are un zerou in s = 0 functia de transfer a buclei in circuit deschis L (L = GC) are un pol in origine, adica G sau C are un pol in origine (caracter integrator).

Conform Teoremei 2 iesirea y urmareste asimptotic o treapta aplicata la intrarea r S 0 0, adica G 0 Q 0 1 . Aceasta ecuatie are o solutie Q RH G 0 0, deci multimea tuturor regulatoarelor stabilizatoare care asigura urmarirea asimptotica a unui semnal treapta este: .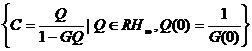

Exemplu pag.104-105

21)Parametrizarea regulatorului (cazul general)

Functia de transfer G nu mai este presupusa stabila. Fie G N/M o factorizare coprima peste RH , iar X si Y doua functii din RH care satisfac ecuatia NX MY 1 (*) .

Teorema: Multimea tuturor regulatoarelor C pentru care sistemul cu reactie este intern stabil este egala cu .

Observatie: Teorema se reduce la Teorema 1 atunci cand G RH In acest caz putem alege: N = G, M = 1, X = 0, Y = 1 si rezulta .

Demonstratia Teoremei se bazeaza pe urmatoarea lema:

Lema: Fie C N_C/M_C o factorizare coprima peste RH . Atunci, sistemul cu reactie este intern stabil ↔ NN_C MM_C RH

Demonstratia Teoremei: (). Se presupune ca Q RH si . Pentru a arata ca sistemul este intern stabil, se definesc si . Atunci, din ecuatia NX MY 1 rezulta ca NN_C MM_C 1.

Deci, C N_C/M_C este o factorizare coprima, iar Lema asigura stabilitatea interna a sistemului cu reactie.

(). Invers, fie C un regulator oarecare asigurand stabilitatea interna. Trebuie sa determinam un Q in RH astfel incat .

Fie C N_C/M_C o factorizare coprima peste RH si definim astfel incat

NN_CV MM_CV 1 (1). Din Lema rezulta ca V RH Fie Q solutia ecuatiei M_CV Y NQ (2

Inlocuind (2) in (1) se obtine NN_CV M Y NQ 1. (3) De asemenea, adunand si scazand termenul NMQ in (*) se obtine N X MQ M Y NQ (4)

Comparand (3) si (4) rezulta N_CV X MQ (5) si tinand cont de (2) se obtine .

Pentru a arata ca parametrul Q RH se multiplica (2) cu X si (5) cu Y, apoi se scad relatiile obtinute. Rezulta NX MY Q YN_CV XM_CV sau, tinand cont de (1) Q YN_CV XM_CV deci, Q RH .

Exemplu pag.107-109

22)Stabilizare tare. Stabilizare simultana

Se spune ca o instalatie este tare stabilizabila daca stabilizarea interna poate fi obtinuta cu un regulator stabil.

Exemplu pag.109-110

Teorema: G este tare stabilizabila ↔ aceasta are un numar par de poli reali intre fiecare pereche de zerouri reale din Re s 0.

Observatie: Punctul s este inclus printre zerourile reale ale lui G.

Exemple pag.110-111

Doua instalatii G₁ si G₂ sunt stabilizabile simultan daca stabilitatea interna este obtenabila pentru ambele printr-un regulator comun.

Se considera factorizarile coprime: Gi Ni/Mi , NiXi MiYi 1, i 1, 2 si se definesc

N N₂M₁ N₁M₂ , M N₂X₁ M₂Y₁ , G N/M .

De exemplu, daca G₁ este deja stabila, se poate lua N₁ G₁ , M₁ 1, X₁ 0, Y₁ 1 si se obtine

N N₂ G₁M₂ , M M₂ astfel incat G G₂ G₁ .

Teorema: G₁ si G₂ sunt stabilizabile simultan ↔ G este tare stabilizabila.

Exemplu pag.111