Masini cu Stari Finite Nedeterministe

Masini cu Stari Finite Nedeterministe

Fie L un limbaj. Exista o masina cu stari finite M astfel incat L = L(M) daca si numai daca exista o gramatica regulara G astfel ca L=L(G).

Demonstratia necesitatii teoremei de mai sus este imediata. Data fiind o gramatica G, construim o masina cu stari finite M care accepta L(G), punand neterminalele sa joace rolul starilor si incluzand tranzitia A→B (δ(A,a)=B) pentru fiecare productie de forma A→ aB. Cu toate acestea, dupa cum arata exemplul urmator, idea nu aduce rezultatul dorit.

Fie G gramatica

S → aA A → aB B→b

S → bB A → aS.

Daca incercam sa construim masina potrivita schemei indicate, apar doua dificultati. Mai intai, ce ar trebui sa fie δ(B,a)? Nu exista o productie de forma B → aX pentru niciun neterminal X. Mai tarziu vom vedea ca acesta este doar un inconvenient ce poate fi eliminat. Mult mai serioasa este problema ce apare la productiile A → aB sau A → aS. In incercarea construirii masinii M apare dilema definirii lui δ(A,a), de pilda, ce e de facut cand M se afla in starea A si citeste simbolul a? Productia A→ aB implica, ca urmatoarea stare δ(A,a) sa fie B, in timp ce A → aS sugereaza sa fie S. Prin urmare, fragmentul diagramei de descriere a M va arata ca in figura de mai jos:

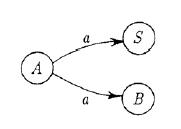Diagrama de tranzitie la ambiguitate

La definirea masinii cu stari finite (in prima definitie), s-a precizat ca δ(Q,x) a fost definita pentru fiecare stare Q in parte si orice simbol de intrare x, iar cunoscand Q si x stim starea urmatoare, de exemplu, valoarea functie de tranzitie δ(Q,x) a fost unic definita. Masina nu a fost lasata sa faca nicio alta alegere. O modalitate de iesire din acest impas este de a extinde definitia unei masini cu stari finite, permitand includerea particularitatilor descrise mai sus. Astfel de dispozitive vor fi numite automate finite nedeterministe (AFN) sau masini cu stari finite nedeterministe (MSFN). Observam ca fiind data o masina de acest gen, M, exista un automat finit determinist obisnuit care accepta acelasi limbaj ca M.

O masina cu stari finite nederminista (MSFN) se compune din urmatoarele cinci obiecte:

1. O multime finita, nevida Q= stari.

2. O multime finita, nevida Σ= simboluri de intrare admise (alfabetul).

3. O stare desemnata Q Q, numit stare initiala.

4. O functie de tranzitie δ(Q,x), care nu trebuie definita pentru toti Q din Q si x din Σ. Pentru acei Q si x pentru care ste definita, δ(Q,x) desemneaza o multime de una sau mai multe stari din Q. Concret, daca β(Q) este multimea tuturor submultimilor din Q, atunci functia de tranzitie este δ : Q x Σ → β(Q). Cu aceasta notatie, (Q,x) "nu e definita" inseamna (Q,x) = Ø (multimea vida). Functia δ se interpreteaza la fel ca in cazul determinist: starea urmatoare. Diferenta este doar ca admite mai multe posibilitati (sau nici una).

5. O multime nevida F de stari. Elementele din F se numesc stari acceptate sau finale.

Aceste masini M vor fi notate (ca masinile deterministe) si se mai numesc automate finite nedeterministe (AFN). Asadar, totul e la fel ca in cazul determinist, cu exceptia definirii functiei de tranzitie δ. Miscarile unui MSFN sunt date de felul urmator.

1. Fiind dat un sir σ = x x xp de simboluri de intrare din Σ, configuratia initiala va fi Q , x x xp, unde M este in starea initiala Q , cu simbolul de intrare x

2. Presupunem ca la un moment dat, configuratia M este Q, xixi+1xp. Daca Q' este una din valorile posibile ale lui δ(Q,x) (mai exact, Q' δ(Q,xi)) atunci M poate trece in configuratia Q', xi+1xp. Deci, daca M se afla in starea Q si simbolul de intrare este x, M poate trece in orice stare din δ(Q,x), dar nu in alta. Cand δ(Q,xi) = Ø nu se va face nicio miscare. Daca e posibila, trecerea de la o configuratie la alta, se numeste miscare legala si este notata prin

Q, xixi+1xp → Q', xi+1xp

3. Masina se opreste daca a citit intregul input (in configuratia Q,λ) sau cand δ(Q,xi) = Ø (δ(Q,xi) nu contine posibilitati pentru urmatoarea stare).

Exemplu. Fie M o MSFN dupa cum urmeaza. Multimea starilor Q are patru elemente: Q = , alfabetul Σ = , starea initiala este Q si multimea starilor finale F = .

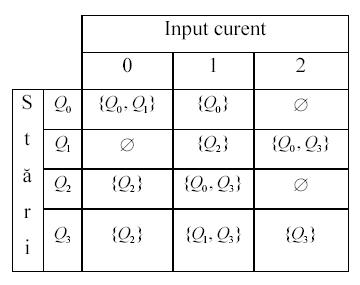
O functie de tranzitie nedeteminista δ.

O MSFN.

Functia de tranzitie este data de tabelul sau de diagrama de mai sus. Astfel, daca masina se afla in starea Q si simbolul de intrare este 2, M poate trece in starile Q sau Q . Ca urmare, dat fiind un input σ, masina M poate trece prin diferite secvente de miscari. De exemplu, pentru o = 01021 unele dintre miscarile posibile sunt urmatoarele:

Q , 01021 → Q , 1021 → Q , 021 → Q , 21 → Q , 1 → Q , λ - stop

Q , 01021 → Q , 1021 → Q , 021 → Q , 21 - stop

Q , 01021 → Q , 1021 → Q , 021 → Q , 21 - stop

Q , 01021 → Q , 1021 → Q , 021 → Q , 21 → Q , 1 → Q , λ - stop

In prima secventa, input-ul este citit in intregime dar masina se opreste intr-o stare neacceptata; in a doua si a treia secventa, M se opreste inainte ca sirul sa fie citit in intregime; si in a patra secventa, intregul sir este citit iar ultima stare este o stare acceptata.

Daca Q, σ si Q', σ' sunt doua configuratii, astfel incat M poate trece din Q, σ in Q', σ' printr-o secventa de miscari admise, spunem ca Q', σ' este derivabil din Q, σ si notam aceasta

Q, → Q',

In exemplul anterior avem Q , 01021 →* Q , 21 si Q →* Q , λ. Putem defini acum un limbaj generat (acceptat, recunoscut) de o masina cu stari finite nedeterminista.

Fie M = o MSFN. Spunem ca un sir σ = x x xp de elemente din Σ este acceptat de M daca

Q , x x xp →* Q, λ

si Q Є F. Multimea sirurilor acceptate de M se noteaza L(M) si se numeste limbaj generat de M.

Observam ca, pentru ca un sir σ o sa fie acceptat de M, avem nevoie doar de o secventa legala de miscari din Q , σ in Q, λ, unde Q este o stare acceptata; nu toate secventele legale vor fi folosite aici. In primul exemplu Q Q , λ, deci σ = 01021 este in L(M) deoarece Q este o stare acceptata. Chiar daca masina porneste in configuratia Q , 01021, ea poate ajunge in mai multe impasuri:

Q , 01021 →* Q , 21, Q , 01021 → Q , 21, etc.

Evident ca masinile cu stari finite din prima definitie sunt cazuri particulare ale masinilor nedeterministe. Ele se caracterizeaza prin faptul ca pentru fiecare stare Q si pentru fiecare input x multimea δ(Q,x) este formata dintr-o singura stare. Din acest motiv e de asteptat ca clasa acceptata de masinile deterministe, de exemplu, sa existe o MSFN M, astfel incat pentru nicio masina determinista K sa avem L(M) = L(K). Totusi, acesta nu va fi cazul.

Fie M o masina cu stari finite nedeterminista. Atunci exista o masina determinista K astfel incat L(M) = L(K); masinile M si K accepta acelasi sir.

Demonstratie. Fie o masina cu stari finite nedeterminista M. Fie Q = o multime de stari din M, cu Q starea initiala, Σ = alfabetul, δ functia de tranzitie si F multimea starilor acceptate. Masina K specifica:

1. Alfabetul de intrare pentru K este - acelasi ca la M.

2. Starile din K vor fi toate submultimile posibile din Q. Spre exemplu, daca M are trei stari - Q , Q si Q - starile din K vor fi S = , S = , S = , S = , S = , S = , S = si S = Ø - multimea vida. (Multimea vida se include ca submultime a fiecarei multimi.) Asadar, daca M are n stari masina K va avea 2 la puterea n stari. Multimea strailor din K se noteaza cu S.

3. K are starea initiala S = , unde Q este starea initiala din M.

4. O stare S S va fi stare finala in K daca si numai daca contine o stare finala Q F din M. Spre exemplu, considerand masina M din exemplul anterior, starile finale pentru K vor fi multimile care contin Q sau Q (respectiv ambele). Acestea sunt , , , , , , , , , , , .

5. Functia de tranzitie Δ pentru K este definita in felul urmator. Fie S = o stare din K si x Σ. Valoarea Δ(S, x) corespunde altei stari K, de exemplu, o multime de Q-uri definite dupa regula:

Daca Q δ(Qj, x) pentru unii Qj din S atunci Q Δ(S, x)

Formal avem

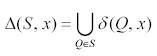
Altfel spus, daca pentru unii Qj din S masina M poate trece la input-ul x din starea Qj in Q, atunci Q Δ(S, x). O nedeterminare apare cand S = Ø (care este o stare din K). Formal, aceasta nu reprezinta o problema, deoarece ne va rezulta in acest caz Δ(Ø, x) = Ø oricare ar fi x (o reuniune de multimi vide este vida)..

Asadar, masina K este complet definita si evident determinista: Pentru fiecare stare S din K si fiecare simbol de intrare x, functia Δ(S, x) defineste in mod unic alta stare K.

Pentru a demonstra ca L(K) = L(M), presupunem ca un sir = x ,x ,xp este acceptat de M. Aceasta inseamna ca pentru o secventa de stari Q , Q' , Q' , , Q'p secventa de miscari

x x xi+1    xp

Q = Q' → Q' → Q' → → Q'i → Q'i+1 → → Q'p-1    → Q'p

este legala, iar Q'p este o stare acceptata din M. Rezulta ca pentru fiecare i = 0, 1, 2, , p-1, functia de tranzitie δ satisface

Q'i+1 Є δ(Q'i, xi+1), i = 0, 1, , p-1

Cand sirul este introdus in masina K, masina executa urmatoarea secventa de miscari:

x x xi+1 xp

S = S' → S' → S' → → S'i → S'i+1 → → S'p-1 → S'p

x

Pentru i = 0, Q' este in δ (Q' , x ), deoarece Q' → Q' este o tranzitie legala in M, astfel Q' este in S' (S' , x ). Analog, cu i = 1, Q' este in δ (Q' , x ), deci Q' S' (S' , x ). Continuand astfel, observam ca Q'j este in S'j oricare ar fi j, in particular Q'p S'p. Q'p fiind o stare finala in M (σ a fost acceptat de M), constatam ca S'p este o stare finala in K, σ este acceptat de K.

Reciproc, presupunem ca un sir σ = x , x , , xp este acceptat de K, si fie secventa de miscari expusa precedent, secventa de miscari facuta de L la input-ul σ. Pentru fiecare Q' S' miscarea Q' → Q' este legala pentru masina M. Analog, pentru fiecare Q' S' exista un Q' in S' astfel incat secventa de miscari

x x

Q' → Q' → Q'

Este legala in M. Alegem Q' ca fiind starea pentru care tranzitia Q' → Q' este legala. In acelasi mod aratam ca daca Q' S' , atunci putem gasi Q' S' si Q' S' astfel inca Q' → Q' → Q' → Q' este o secventa legala de miscari.Continuand astfel, observam ca pentru fiecare Q'p si S'p putem gasi Q' S' , Q' S' , , Q'p-1 Є S'p-1 astfel incat sa rezulte o secventa legala de miscari din M. Daca acum alegem Q'p din S'p, care este o stare acceptata din M, constatam ca σ este acceptat de M, adica face parte din limbajul L(M).

Fie M si M doua MSF. Masinile M si M se numesc echivalente daca genereaza (accepta) acelasi limbaj, L(M ) = L(M

Fie M = o MSFN (masina cu stari finite nedeterministe) astfel incat pentru fiecare Q Q si x Σ multimea δ(Q,x) este vida sau contine un singur element. Fie K o masina obtinuta din M prin adaugarea unei stari noi D, si a carei functie de tranzitie Δ este definita dupa cum urmeaza:

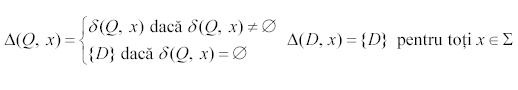
Starile finale si initiale din K sunt aceleasi ca si in M - in particular D nu este o stare acceptata. Atunci K este o masina determinista si echivalenta cu M.

Starea D introdusa mai sus are intelesul de "capcana" sau stare "moarta". Daca masina M se blocheaza intr-o stare oarecare, sirul σ citit nu poate fi acceptat. Totusi se trimite masina in acea stare "moarta".

Bibliografie:

An Introduction to Formal Languages and Automata

- Peter Linz

An Introduction to the Theory of Formal Languages and Automata

Willem J. M. Levet

regielive.ro