 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
Circuite de impulsuri
1. Generalitati
Impulsul este un semnal a carui forma de unda variaza prin salturi fata de un nivel stationar sau cvasistationar , durata salturilor fiind mult mai mica decat durata regimului tranzitoriu de raspuns al circuitului , la intrarea caruia se aplica impulsul .
In Fig. 1. sunt reprezentate o serie de impulsuri video periodice ideale si anume : tip meandre (a) , triunghiulare simetrice (b) , trapezoidale simetrice (c) , exponentiale (d) , dreptunghiulare (e) , precum si impulsuri radio dreptunghiulare periodice , ideale (f) .
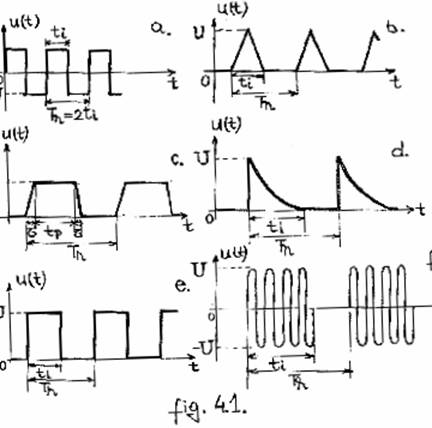
Impulsurile radio se obtine prin modularea unei oscilatii armonice cu ajutorul impulsurilor video . In Fig.1. cu ti s-a notat durata impulsurilor , cu Tr perioada de repetitie a acestora , cu tp timpul de palier , cu U amplitudinea impulsurilor iar cu τ timpii de crestere respectiv descrestere .
Cele mai folosite in practica sunt impulsurile video dreptunghiulare . Principalii parametri ai impulsului video dreptunghiular singular sunt ilustrati in Fig. 2.
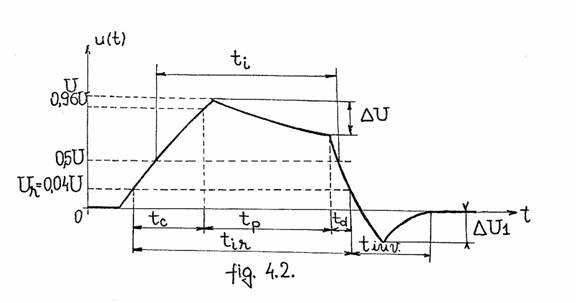
Amplitudinea se noteaza cu U si reprezinta valoarea maxima la care ajunge tensiunea in impuls .
Caderea
de amplitudine pe palier reprezinta variatia descrescatoare
maxima a tensiunii pe durata palierului impulsului . Se noteaza cu ![]()
![]() si se apreciaza
de obicei in procente fata de amplitudinea U a impulsului .
si se apreciaza
de obicei in procente fata de amplitudinea U a impulsului .
Caderea
de amplitudine postimpuls reprezinta variatia descrescatoare
maxima a tensiunii dupa terminarea impulsului propriuzis , fata de nivelul
stationar inferior . Se noteaza cu ![]() si de regula este
egala cu caderea de tensiune pe palier .
si de regula este
egala cu caderea de tensiune pe palier .
Durata impulsului reprezinta
intervalul de timp in care semnalul depaseste un nivel de
referinta ![]() dat de retea :
dat de retea :
![]() (1)
(1)
Durata impulsului astfel determinata se noteaza tir iar pentru
r =0,04 se asigura simplificarea unor relatii de calcul ulterioare .
Durata efectiva a impulsului se noteaza cu ti , corespunde valorii r = 0,5 si reprezinta durata unui impuls dreptunghiular ideal care are aceeasi energie cu impulsul dreptunghiular real din Fig. 2.
In continuare , prin durata impulsului se va intelege durata efectiva a acestuia .
Timpul
de crestere al impulsului tc reprezinta intervalul de timp in care
semnalul de la nivelul stationar minim la cel maxim , cu valorile aproximate
la ![]() respectiv (1-r)U .
respectiv (1-r)U .
In continuare , se va considera r = 0,04 caz in care timpul de crestere este dat de relatia :
![]() (2)
(2)
Timpul de palier tp al impulsului este
intervalul de timp in care semnalul in impuls nu scade sub valoarea ![]() .
.
Timpul de descrestere td al impulsului este intervalul in care semnalul variaza de la nivelul corespunzator sfarsitul palierului pana la nivelul stationar minim .
Puterea in impuls Pi este energia disipata pe durata acestuia :
![]()
si este data de produsul amplitudinilor tensiunii si curentului .
Ca elemente active , circuitele de impulsuri pot folosi tuburi electronice , tranzistoare bipolare sau unipolare , tiristoare , etc. In acest capitol se vor analiza exclusiv circuitele de impulsuri cu tranzistoare bipolare . Pe langa elementele de circuit active , circuitele de impulsuri contin si subcircuite pasive de ordinul I de tip RC sau RL .
In practica se intalnesc aproape exclusiv circuite de ordinul I de tip RC.
2. Circuitele RC de ordinul I in regim de impulsuri
Deoarece contin un singur element de circuit reactiv (bobina sau condensator) , circuitele de ordinul I sunt descrise printr-o ecuatie diferentiala de ordinul I cu coeficienti reali , astfel:
![]() (3)
(3)
unde x(t) este semnalul de intrare (excitatia)
, y(t) este semnalul de iesire (raspunsul ) iar ![]() este constanta de timp
a circuitului .
este constanta de timp
a circuitului .
Solutia de regim liber a ecuatiei (3) este de forma :
![]() (4)
(4)
unde A este o constanta de integrare iar ![]() este solutia ecuatiei
caracteristice .
este solutia ecuatiei
caracteristice .
In mod frecvent , excitatia este un semnal treapta :
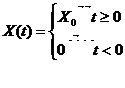
caz in care solutia de regim fortat este data de relatia :
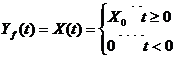
Solutia globala a ecuatiei diferentiale de ordinul I este :
![]() (5)
(5)
Din relatia de mai sus pentru ![]() se obtine
se obtine ![]() si (5) devine :
si (5) devine :
![]() (6)
(6)
Cunoscand valoarea initiala Y(0) , din (6) pentru t=0 se obtine valoarea constantei de integrare :
![]()
si in final solutia ecuatiei (3) devine :
![]() (7)
(7)
In
practica este necesar sa se determine intervalul de timp ![]() , in care raspunsul
circuitului evolueaza de la nivelul
, in care raspunsul
circuitului evolueaza de la nivelul ![]() la nivelul
la nivelul ![]() .
.
Din (7) rezulta :
![]()
![]()
![]()
si deci:
Daca se considera:
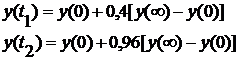
Folosind (8) se poate justifica
relatia (2), astfel:
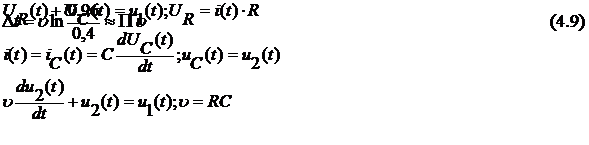
In Figura 3.a este reprezentat un circuit Rc de integrare pentru care
avem succesiv:
![]()
Daca circuitul de integrare este excitat cu un semnal treapta
(Fig.3.b). dat de:
raspunsul este dat de relatia (7):
![]()
Considerand ca la momentul t=0, condensatorul este complet
descarcat UC(0)=0, iar la momentul t=∞ el este complet
incarcat, UC(∞)=U, se obtine:
Raspunsul (10), al circuitului de integrare la un semnal treapta este redat in Fig. 3 c pentru doua valori υ si υ' ale constantei de timp.
Integrala unuisemnal treapta este un semnal rampa.
Circuitul din Fig. 3a se apropie de un integrator ideal atunci cand constanta de timp υ=RC are valori foarte mari , caz in care condensatorul C se incarca cvasiliniar.
![]()
Din (9) rezulta ca timpul de crestere al raspunsului
de la 0,4U la 0,96U este:
In domeniul frecventa, circuitul de integrare se conporta ca un FTJ. Intr-adevar, prin atenuarea frecventelor inalte din spectrul semnalului treapta, se elimina saltul instantaneu al acestuia de la 0 la U iar raspunsul u2(t) prezinta o crestere mult mai lenta intre cele doua nivele. Prin analogie cu Fig. 1.9.c, circuitul de integrare poate fi considerat ca o semicelula Rc de filtrare "trece jos".

![]()
![]()
![]()
![]()
![]()
![]()
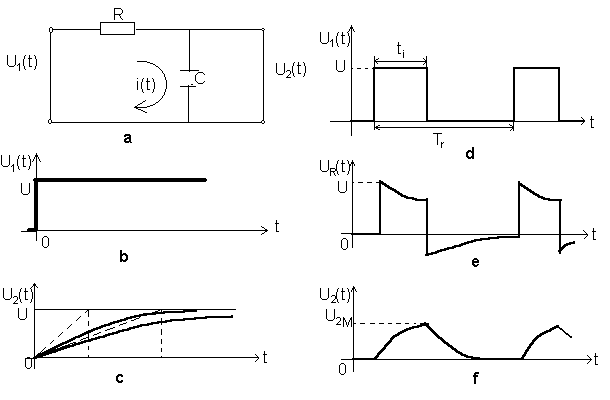
![]() Figura 3
Figura 3
Daca excitarea circuitului de integrare se face cu impulsuri dreptunghiulare (Fig. 3.d) raspunsul (Fig. 3.f) se obtine aplicand principiul superpozitiei (impulsul dreptunghiular de la intrare se descompune intr-o suma de semnale treapta decalate in timp cu ti si de polaritate diferita).
![]()
Pentru o durata tI data a impulsurilor, circuitul
are efect integrator daca:
![]()
In plus, pentru a nu se realiza deplasarea nivelului componentei continue la iesire, trebuie ca:
ceea ce permite descarcarea completa a condensatorului in pauza dintre impulsuri.
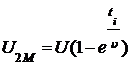
Amplitudinea maxima a semnalului de iesire rezulta din (10):
Circuitul de integrare realizeaza deci o largire a impulsurilor dreptunghiulare si o reducere a amplitudinii acestora.
In circuitele de impulsuri, timpii de crestere si de scadere ai semnalelor in impuls sunt determinati de efectul integrator al capacitatilor parazite dispuse in paralel pe calea de semnal.
![]()
![]()
In Fig. a este reprezentat un circuit RC de derivare (diferentiere) pentru care semnalul de iesire se culege de pe rezistenta R:
U2(t)=UR(t)=U1(t)-UC(t)
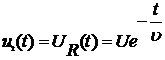
Tensiunea pe condensator este data de (10) iar excitatia este un semnal treapta si deci:
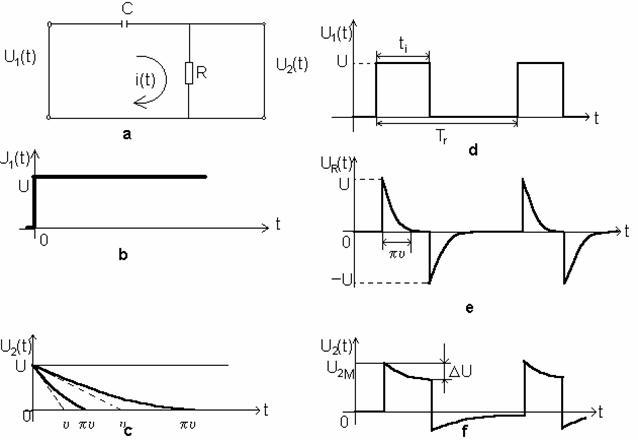
Raspunsul circuitului de derivare la
un semnal treapta este reprezentat in Fig. c pentru doua valori
υ si υ' ale constantei de timp.
Derivata unui semnal treapta este un impuls Dirac ponderat cu valoarea discontinuitatii din origine Uδ(t). Circuitul din Fig.a se apropie de un circuit de derivare ideal pentru valori foarte mici ale constantei de timp
υ =RC.
Timpul de descrestere al raspunsului U2(t) de la 0,96U la 0,4U este:
In domeniul frecventa circuitul de derivare se comporta ca un F.T.S. Daca excitarea circuitului se face cu impulsuri periodice dreptunghiulare (Fig. d) raspunsul se obtine tot prin aplicarea principiului superpozitiei. Pentru a ramane un circuit de derivare si in regim de impulsuri, trebuie indeplinita conditia:
![]()
Pentru a se evita deplasarea nivelului in curent continuu trebuie
indeplinita conditia (12).In final, constanta de timp a circuitului
de derivare este limitata de relatia:
Circuitul de derivare realizeaza o ingustare a impulsurilor dreptunghiulare pe care le transforma in impulsuri bipolare cu amplitudini si durate egale (fi. e).
![]()
Daca
circuitul din Fig.a devine un circuit de cuplaj de tip RC. Deoarece circuitul de cuplaj este destinat sa elimine componenta de curent continuu (Fig.f) trebuie ca Пυ>Tr- ti.
![]()
Constanta de timp a circuitului de cuplaj trebuie deci sa
indeplineasca conditia:
Пυ>max.
Caderea de amplitudine pe palier ΔU reprezinta nivelul de tensiune la care se incarca condensatorul C pe durata ti si conform (10) se obtine:
Marimea ΔU reprezinta distorsiunea introdusa de circuitul de cuplaj Rc si poate fi micsorata prin cresterea capacitatii condensatorului de cuplaj in conditiile in care rezistenta R este de obicei data.
In circuitele de impulsuri, efectul de derivare si distorsiunile datorate caderii de tensiune pe palier sunt produse de condensatoarele dispuse in serie pe calea de semnal (condensatoare de cuplaj).
3. Tranzistorul bipolar in regim de comutatie
La functionarea in regim de impulsuri tranzistorul bipolar se poate gasi intr-una din urmatoarele stari:
blocari, in care curentul de colector IC este foarte mic, practic egal cu zero, iar tensiunea UCE are valori apropiate de tensiunea de alimentare EC;
conductie, in care curentul de colector IC are valori mari iar tensiunea UCE este redusa (in cele mai multe cazuri tranzistorul este in saturatie);
comutare directa, in care curentul de colector IC creste rapid iar tranzistorul trece din stare de conductie in stare de blocare.
Cea mai simpla schema de circuit de comutatie cu tranzistor bipolar este reprezentata in Fig. 5a. iar in Fig.5b. sunt redate caracteristicile de iesire ale unui tranzistor bipolar in montaj EC si dreapta de sarcina.
Regiunea de blocare corespunde situatiei in care ambele jonctiuni ale tranzistorului sunt polarizate invers si este cuprinsa intre caracteristica corespunzatoare la IB=0 si abscisa.
Regiunea activa normala corespunde situatiei in care jonctiunea B-E este polarizata direct si jonctiunea B-C invers si este dispusa intre regiunile de blocare si respectiv de saturatie, hasurate in Fig.5b.

Regiunea de saturatie corespunde situatiei in care ambele
jonctiuni ale tranzistorului sunt polarizate direct si este
delimitata de o dreapta paralela cu ordonata corespunzatoare
tensiunii UCES, numita a si tensiunea de
saturatie incipienta.
In saturatie UCE<UBE, valorile tipice ale acestor tensiuni, la limita de saturatie pentru un tranzistor npn cu SI fiind UCES= 0,3V si UBES =0,7V.
Curentul de colector la limita de saturatie este dat de relatia:

In saturatie curentul de colector nu mai urmareste
cresterea curentului de comanda din baza tranzistorului deci:
de unde, tinand cont de (1), rezulta:
Ultima relatie reprezinta un criteriu de saturatie a tranzistorului bipolar. Punctul static de functionare M1 al tranzistorului se alege in regiunea de blocare, pentru consum minim de energie in stare neexcitata. In regim de comutare normala, amplitudinea impulsului pozitiv de intrare determina deplasarea punctului de functionare in M2, pe caracteristica IB<IBS, in regiunea activa normala.
In regim de comutatie fortata, tranzistorul comuta din blocare in saturatie, intre punctul M1 si punctul M4 dispus pe caracteristica IB>IBS. Pentru aceasta, amplitudinea Uin a semnalului in impuls de la intrare (Fig.5c.), trebuie sa fie suficient de mare ca sa determine un curent de baza IB<IBS ≈E/βRC.
Curentul de baza IB ia valoarea IB cu o intarziere tb fata de momentul aplicarii excitatiei, datorita descarcarii capacitatilor de bariera ale celor doua jonctiuni, polarizate invers in starea initiala de blocare a tranzistorului ( la polaritate inversa capacitatea unei jonctiuni este practic egala cu capacitatea de bariera).
La randul lui, curentul de colector Ic incepe sa creasca cu o intarziere tdf necesara pentru difuzia purtatorilor de sarcina injectati in baza. Aceasta intarziere poate fi interpretata ca fiind timpul necesar pentru incarcarea capacitatii de difuzie a jonctiunii B-E polarizata direct (la polarizare directa capacitatea de bariera devine neglijabila in raport cu cea de difuzie). Suportul fizic al cresterii curentului de colector la valoarea IC este dat de sarcina acumulata in baza, din care acesta se formeaza. Timpul de crestere tc al curentului de colector este necesar pentru acumularea sarcinii in baza si determina caracterul integrator al tranzistorului bipolar fata de excitatie.
![]()
Se numeste grad de saturatie
si se noteaza cu S, raportul dintre valoarea maxima a curentului
de baza si valoarea maxima a curentului de baza
corespunzatoare zonei de saturatie incipienta:
![]()
In [13] se arata ca timpul de crestere tc la
comutatia fortata este:
unde υe reprezinta constanta de timp echivalenta ce caracterizeaza efectul integrator al tranzistorului de combatere normala.
Din (16) rezulta scaderea timpului de crestere atunci cand se mareste gradul de saturatie al tranzistorului.
![]()
Timpul necesar comutarii directe a tranzistorului este:
deoarece tb si tdf au valori uzuale de ordinul nanosecundelor.
Fig.5.
In comutare directa fortata punctul dinamic de functionare parcurge segmentul M1M4 pe dreapta de sarcina in baza. Din aceasta cauza scaderea curentului de baza nu determina scaderea imediata a curentului de colector.
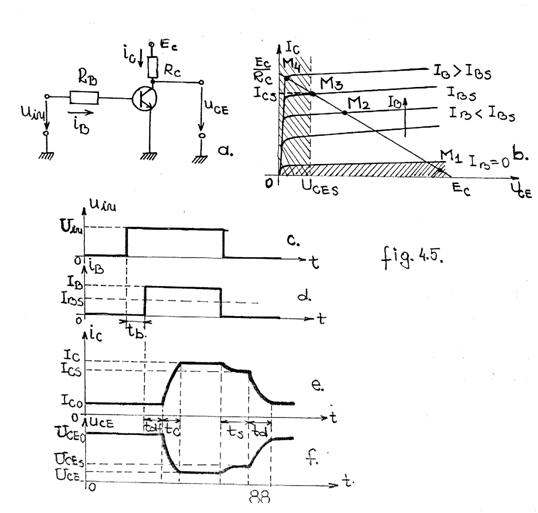
In acest interval de timp , punctul dinamic parcurge segmentul M4M3 pe dreapta de sarcina iar curentul de colector scade foarte putin. In [15] se arata ca timpul de stocare ts se reduce atunci cand curentul de comanda iB devine negativ, proportional cu marimea saltului negativ al acestuia. Timpul de descrestere td al curentului de colector este necesar evacuarii sarcinii stocate in baza si poate fi redus in acelasi fel ca ts.
Timpul de comutare inversa este deci:
![]()
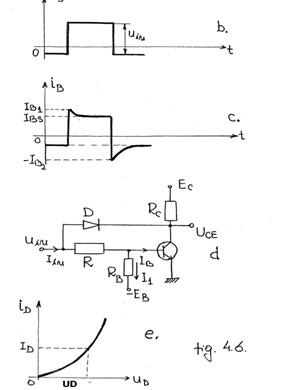
Diagramele de timp din Figura 5. indica faptul ca circuitul de comutatie din Fig. 5 poate fi considerat un amplificator de impulsuri care determina insa o largire a impulsului de iesire fata de cel de intrare datorita timpilor de comutare tcd si tci. OO cale de reducere a timpilor de comutare (Fig.6.a) consta in introducerea unei surse negative de polarizare care reduce tci si a unei surse negative de polarizare care reduce tci si a unui grup RC numit de accelerare care reduce tcd prin cresterea gradului de saturatie S.
La momentul aplicarii excitatiei, condensatorul C scurtcircuiteaza rezistenta R si curentul de comanda are valoarea IB1>IBS, ceea ce reduce timpul de crestere tc al curentului de baza ar creste timpul de stocare ts dar la incarcarea condensatorului curentul de baza se reduce si ajunge la valoarea IBS corespunzatoare zonei de saturatie incipienta atunci cand C este complet incarcat si nu mai scurtcircuiteaza rezistenta R. La comutarea inversa, a tranzistorului, prin descarcarea condensatorului se asigura un salt negativ - IB2 al curentului in baza care reduce atat timpul de stocare IBS cat si timpul de descrestere.
Reducerea in principal a timpului de comutatie inversa tci se poate obtine cu circuitul din Figura 6d care evita intrarea in saturatie a tranzistorului printr-o reactie negativa neliniara.
Rezistenta R se calculeaza astfel incat atunci cand iB atinge valoarea IBS corespunzatoare intrarii in saturatie dioda D sa se deschida si sa limiteze curentul de baza. Pentru acesta tensiunea pe rezistenta trebuie sa fie mai mare decat caderea de tensiune pe dioda:
![]()
unde UD se determina din caracteristica statica a diodei pentru ID=Iin- ( IBS + I1). In acest fel. La comutarea directa, tranzistorul se mentine la limita zonei de saturatie (punctul M3 de functionare din Figura 5b).
Circuitul basculant bistabil
In cadrul circuitelor de impulsuri, o pondere importanta o detin circuitele basculante. Acestea sunt circuite de comutatie caracterizate prin doua stari de echilibru, formate din doua etaje de amplificare in impuls conectate in cascada si prevazute cu o bucla de reactie.
Circuitele basculante pot fi realizate in tehnologie discreta (folosit in prezent pe scara redusa) sau in tehnologie integrata.
Circuitul basculant bistabil (CBB) este caracterizat prin aceea ca ambele stari de echilibru sunt stabile si in consecinta, comutarea intre cele doua stari stabile se face doar la o comanda externa. In Fig. 7a se prezinta cel mai simplu CBB obtinut prin conectarea in cascada a doua etaje de amplificare in impuls inversoare, de tipul celui din Fig. 5a. Cuplajul intre etaje este rezistiv iar bucla de reactie pozitiva se realizeaza prin conectarea iesiri celui de-al doilea etaj la intrarea primului. Caracteristica de transfer a amplificatorului in lipsa reactiei este reprezentata cu linie continua.
Pentru u1<u1' tensiunea in baza lui T1 este sub nivelul de deschidere, acesta este blocat si tensiunea sa mare din condensator il mentine pe T2 in saturatie iar u2 are o valoare redusa. Pentru u1'<u1<u1'', T1' comuta din blocare in conductie, tensiunea sa in colector scade si produce intrarea in blocare a lui T2 iar u2 va creste. Pentru u1>u1'', T1 este saturat, T2 este blocat si u2 are o valoare apropiata de EC. Inchiderea buclei de reactie implica u1=u2, locul geometric al punctelor care indeplinesc aceasta conditie fiind dreapta reprezentata punctat in Fig. 7.b. Din cele trei puncte de intersectie astfel obtinute, doar A corespunzator starii T1- blocat si T2 - saturatie si C (T1 - conductie si T2 - blocat) sunt stabile. In Fig.8.a. se prezinta schema modificata topologic a CBB simetric, prevazut cu intrarile de comanda in raza iar in Fig.8.b. digramele de functionare ale acestuia. S-a considerat starea initiala a CBB ca fiind T1 - blocat si T2 - saturat. La aplicarea unui impuls de comanda pozitiv in baza lui T1 cu amplitudinea suficienta cu tensiunea in baza sa depaseasca nivelul de prag de deblocare, T1 intra in conductie, tensiunea lui scade, scaderea tensiunii uc1 se transmit in baza lui T2 care iese din saturatie
Tensiunii uC2 se transmite in baza lui T1 si determina deschiderea si mai accentuata a acestuia astfel incat se formeaza un ciclu regenerativ care determina comutarea CBB in stare stabila: T1 - saturatie,T2 - blocare. In regim de blocare tensiunea din colectorul lui T2 este apropiata de EC si mentine pe T1 in conductie si dupa terminarea impulsului de comanda din baza lui T1.
Bascularea CBB impune ca durata impulsului de comanda sa acopere timpul necesar ca T1 sa comute direct ca T2 sa comute invers:
tic-da >tcd tci
Revenirea CBB la starea stabila initiala se realizeaza printr-un ciclu regenerativ asemanator la aplicarea unui impuls de comanda pozitiv in baza lui T2
Fiind data tensiunea de alimentare EC si alegand punctul
![]()
M3 (UCES,ICS)din
figura 5.bca externa superioara curbei dinamice , se poate determina rezistenta
de colector:
Unde s-a tinut seama ca UCES![]() 0,3V este neglijabila in raport cu tensiunea de alimentare.
0,3V este neglijabila in raport cu tensiunea de alimentare.
![]()
Curentul de baza al tranzistoarelor
este:
Deoarece valoarea maxima de 0,7Vla saturatie , a tensiunii UBE este neglijabila in raport cu EC .
Inlocuind relatia de mai sus in (15) se obtine conditia de saturatie :
RB b-1)RC (21)
Rezistenta RB se determina din (21) considerata la limita, pentru a asigura functionarea in zona incipienta de saturatie.
Deoarece in saturatie tensiunea de colector este 0,3V, tensiunea aplicata prin RB in baza celuilalt tranzistor respecta conditia de blocare.
Amplitudinea impulsurilor culese de pe colectoare este
![]()
![]()
iar pentru schema din figura 8a
rezulta:
In figura 8c se prezinta cu titlu informativ
o schema de CBB cu timpi de comutatie redusi obtinute prin
conectarea la cascada, cu bucla de reactie polara, a doua etaje de
amplificare de tipul celui din 6a. In principal CBB se foloseste ca
element de memorie in sistemele binare in care numerele 0 si 1 sunt echivalente
cu starile de conductie sau blocare in care se poate afla un
tranzistor in regim de comutare. In logica pozitiva, palierul superior al unui
impuls se asociaza cifrei 1 (corespunde nivelului u![]() al tensiunii de colector pentru un tranzistor blocat) iar
palierul inferior al impulsului se asociaza cifrei 0(corespunde nivelului
uc pentru un tranzistor
aflat in conductie)Pentru a amplifica analiza diferitelor tipuri de CBB
s-a realizat o standardizare a acestora. Astfel CBB in figura 8 este un bistabil RS iar tabelul de functionare numit si tabelul de
adevar este redat in fig. 8 d. Cele doua intrari de comanda numite si
intrari de date notat cu R (initiala de la RESET - stergere) si
S (initiala de la SET initializare)iar cele doua iesiri in anti
faza s-au notat Q si (Q negat)
al tensiunii de colector pentru un tranzistor blocat) iar
palierul inferior al impulsului se asociaza cifrei 0(corespunde nivelului
uc pentru un tranzistor
aflat in conductie)Pentru a amplifica analiza diferitelor tipuri de CBB
s-a realizat o standardizare a acestora. Astfel CBB in figura 8 este un bistabil RS iar tabelul de functionare numit si tabelul de
adevar este redat in fig. 8 d. Cele doua intrari de comanda numite si
intrari de date notat cu R (initiala de la RESET - stergere) si
S (initiala de la SET initializare)iar cele doua iesiri in anti
faza s-au notat Q si (Q negat)
Tabelul de adevar ilustreaza in mod sintetic functionarea CBB caracterizata in detaliu de diagramele de impuls din figura 8b.
Intr-adevar, daca CBB se
gaseste la momentul n in starea ![]() (T1 - blocat, T2 - conductie)
si se aplica un impuls la intrarea R (R=1, S=0), acesta
basculeaza la momentul n+1 in starea
(T1 - blocat, T2 - conductie)
si se aplica un impuls la intrarea R (R=1, S=0), acesta
basculeaza la momentul n+1 in starea ![]() . Circuitul bistabil aflat la momentul n in starea Qn=0,
comuta in starea Qn+1=1 daca se aplica un impuls pe
intrarea S (R=0, S=1). In sfarsit, starea CBB ramane
nemodificata, Qn+1=Qn daca R=0 si S=0.
Comanda simultana pe ambele intrari, R=1, S=1 nu este permisa
deoarece s-ar forta intrarea in conductie a ambelor tranzistoare
. Circuitul bistabil aflat la momentul n in starea Qn=0,
comuta in starea Qn+1=1 daca se aplica un impuls pe
intrarea S (R=0, S=1). In sfarsit, starea CBB ramane
nemodificata, Qn+1=Qn daca R=0 si S=0.
Comanda simultana pe ambele intrari, R=1, S=1 nu este permisa
deoarece s-ar forta intrarea in conductie a ambelor tranzistoare ![]() , ceea ce nu este posibil datorita buclei de
reactie pozitive si starea CBB va fi nedeterminata (fie
, ceea ce nu este posibil datorita buclei de
reactie pozitive si starea CBB va fi nedeterminata (fie ![]() , fie
, fie ![]() ).
).
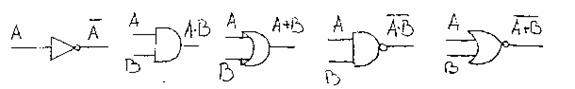
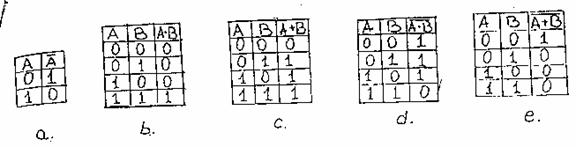
Fig. 9.
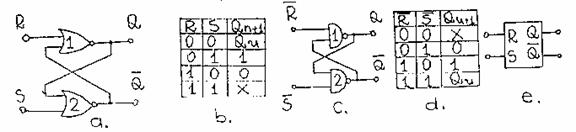
Intr-adevar, conform
tabelului de adevar al functiei ![]() din figura 9e rezulta:pentru R=1 poarta 1 este fortata
in Q=0 indiferent de starea celeilalte intrari iar pentru S=0 poarta 2 are
ambele intrari in 0 si deci.
din figura 9e rezulta:pentru R=1 poarta 1 este fortata
in Q=0 indiferent de starea celeilalte intrari iar pentru S=0 poarta 2 are
ambele intrari in 0 si deci.![]() =1; pentru S=1 poarta 2 este fortata in
=1; pentru S=1 poarta 2 este fortata in ![]() =0 indiferent de starea celeilalte intrari iar pentru
R=0 poarta 2 are ambele intrari in 0 si Q=1; pentru R=0 si Q
=0 indiferent de starea celeilalte intrari iar pentru
R=0 poarta 2 are ambele intrari in 0 si Q=1; pentru R=0 si Q![]() =0 poarta 2 are ambele intrari in 0 si deci
=0 poarta 2 are ambele intrari in 0 si deci ![]() =
=![]() =0 porta 1 cu intrarile 0 si 1, deci va avea
iesirea
=0 porta 1 cu intrarile 0 si 1, deci va avea
iesirea ![]() =
=![]() =0; pentru R=0 si S=0 si Q
=0; pentru R=0 si S=0 si Q![]() =1 poarta 2 are intrarile in 1 si 0, deci
=1 poarta 2 are intrarile in 1 si 0, deci![]() =0 iar poarta 1 cu ambele intrari in 0 isi
mentine iesirea in
=0 iar poarta 1 cu ambele intrari in 0 isi
mentine iesirea in ![]() =
=![]() =1; pentru R=1 si S=1 iesirile ambelor porti sunt
fortate in 0 de aceea aceasta combinatie la intrare nu este admisa .
=1; pentru R=1 si S=1 iesirile ambelor porti sunt
fortate in 0 de aceea aceasta combinatie la intrare nu este admisa .
Prin folosirea portilor ![]() se obtine un bistabil de tip
se obtine un bistabil de tip ![]() (figura 10c). Tabelul
de adevar din figura 10b a acestui
bistabil si notarea intrarilor cu
(figura 10c). Tabelul
de adevar din figura 10b a acestui
bistabil si notarea intrarilor cu ![]() si
si ![]() , indica faptul ca modificarea iesirilor se produce atunci cand una dintre ele este 0
si nu 1 ca in cazul schemei anterioare iar combinatia interzisa la intrare
este acum
, indica faptul ca modificarea iesirilor se produce atunci cand una dintre ele este 0
si nu 1 ca in cazul schemei anterioare iar combinatia interzisa la intrare
este acum ![]() =
=![]() =0.Pentru simplificare, bistabilele de tip RS se
reprezinta simbolic ca in figura 10e. Circuitele basculante ca in figura 10
se numesc asincrone si se caracterizeaza prin aceea ca modificarea intrarilor determina in mod
neconditionat modificarea iesirilor.
=0.Pentru simplificare, bistabilele de tip RS se
reprezinta simbolic ca in figura 10e. Circuitele basculante ca in figura 10
se numesc asincrone si se caracterizeaza prin aceea ca modificarea intrarilor determina in mod
neconditionat modificarea iesirilor.
In figura 11a se prezinta un bistabil RS sincron. Pe langa intrarile date de R si S, acesta este prevazut cu o intrare de tact T care controleaza momentul in care datele aplicate la intrare sunt transferate la iesire . La intrarea de tact se aplica impulsuri dreptunghiulare periodice care asigura functionarea bistabilului in mod sincron cu alte circuite logice in cadrul unui sistem.
Bistabilul RS sincron se
obtine prin completarea schemei![]() asincrone cu doua porti
asincrone cu doua porti ![]() ale caror
intrari R si S sunt validate de semnalul de tact atunci cand T=1, caz in
care la iesirea portilor 1 si 2 se obtin comenzile
ale caror
intrari R si S sunt validate de semnalul de tact atunci cand T=1, caz in
care la iesirea portilor 1 si 2 se obtin comenzile![]() si
si![]() . In plus prin folosirea portilor 3 si 4 de tip
. In plus prin folosirea portilor 3 si 4 de tip ![]() cu trei intrari
se realizeaza doua intrari de comanda asincrone
cu trei intrari
se realizeaza doua intrari de comanda asincrone ![]() si
si ![]() , active cand sunt in
0 si care comanda iesirile indiferent de prezenta sau nu a impulsurilor de
tact. Tabelul de adevar al bistabilului RS sincron este cel din figura 10b
iar simbolul corespunzator este reprezentat in figura 11b.
, active cand sunt in
0 si care comanda iesirile indiferent de prezenta sau nu a impulsurilor de
tact. Tabelul de adevar al bistabilului RS sincron este cel din figura 10b
iar simbolul corespunzator este reprezentat in figura 11b.
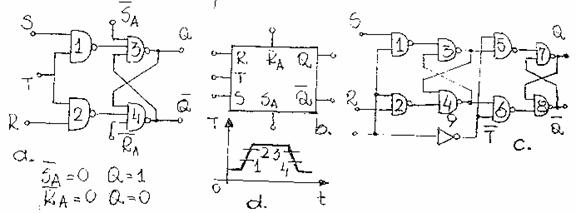
Fig. 11.
O categorie importanta de
bistabile o formeaza cele cu structura stapan-sclav (master-slave).
Ele sunt formate din doua circuite basculante sincrone, conectate in cascada si
comandate in antifaza. In continuare, pentru acest tip de CBB se va utiliza
terminologia "bistabil MS".In figura 11c este reprezentata schema unui bistabil
MS de tip RS (portile 1,2,3 si 4 formeaza bistabilul RS sincron de
comanda sau stapan, portile 5,6,7 si 8 formeaza bistabilul RS
sincron comandat sau sclav, iar inversorul 9 asigura comanda in antifaza a
celor doua bistabile. Impulsul de tact (figura 11d) actioneaza asupra
bistabilului in patru timpi: la momentul unu portile 5 si 6 se
blocheaza (![]() =0)si iesirile bistabilului stapan sunt izolate de
intrarile bistabilului sclav; la momentul 2 portile 1 si 2 se deschid
(T=1)si informatia de la intrarile R si S se transfera la
iesirea bistabilului stapan; la momentul 3 portile 1 si 2 se
blocheaza si bistabilul stapan se izoleaza de intrarile
sale date iar la momentul 4 portile
5 si 6 se deschid si informatia de la iesirile bistabilului
stapan se transfera la bistabilul sclav. Fata de bistabilul RS asincron
simplu, bistabilul de tip MS asigura o mai buna protectie impotriva
comutarilor parazite datorate prezentei perturbatiilor.
=0)si iesirile bistabilului stapan sunt izolate de
intrarile bistabilului sclav; la momentul 2 portile 1 si 2 se deschid
(T=1)si informatia de la intrarile R si S se transfera la
iesirea bistabilului stapan; la momentul 3 portile 1 si 2 se
blocheaza si bistabilul stapan se izoleaza de intrarile
sale date iar la momentul 4 portile
5 si 6 se deschid si informatia de la iesirile bistabilului
stapan se transfera la bistabilul sclav. Fata de bistabilul RS asincron
simplu, bistabilul de tip MS asigura o mai buna protectie impotriva
comutarilor parazite datorate prezentei perturbatiilor.
Asa cum rezulta din
tabelul de adevar din figura 10b, principalul dezavantaj al bistabilului
RS este necesitatea evitarii combinatiei R=S=1l a intrare. Acest
dezavantaj este eliminat de bistabilul JK(J-corespunde intrarii S si
provine de la JAM - forteaza iar K-corespunde lui R si provine de la
KEEP - retine).In figura 12a este reprezentata schema unui bistabil JK asincron
realizat cu porti ![]() Tabelul de adevar
al bistabilului JK este reprezentat in figura 12b si arata ca atunci cand la
intrare apare combinatia J=K =1, interzisa anterior, starea bistabilului
se schimba in Q
Tabelul de adevar
al bistabilului JK este reprezentat in figura 12b si arata ca atunci cand la
intrare apare combinatia J=K =1, interzisa anterior, starea bistabilului
se schimba in Q![]() =
=![]() . Aceasta se poate verifica usor folosind schema
bistabilului JK si tabelul de adevar al functiei logice
. Aceasta se poate verifica usor folosind schema
bistabilului JK si tabelul de adevar al functiei logice ![]() din figura 9d.
Simbolul bistabilului asincron este cel din figura 12c.
din figura 9d.
Simbolul bistabilului asincron este cel din figura 12c.
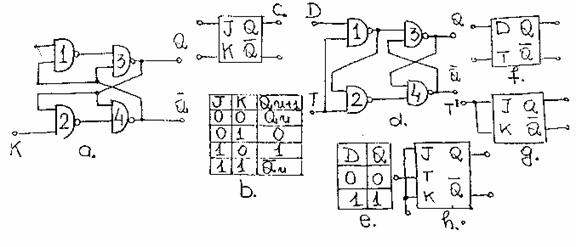
Fig. 12.
La fel ca bistabilul RS si
bistabilul JK poate fi realizat in structura sincrona sau de tip MS avand
eventual si intrari de comanda asincrone. Un tip de bistabil sincron
folosit in practica ca element de memorie tampon in sistemele de afisaj,
este bistabilul D (provine de la DELAY - intarziere). Acest tip de bistabil are
o intrare de tact T si o singura intrare de date, notata cu D si care este reprodusa la iesire pe durata
impulsului de tact T=1, conform tabelului de adevar din figura 12e .
Bistabilul D (figura 12d) poate fi obtinut dintr-un bistabil RS
sincron(figura 11a) fara intrari de comanda asincrone, comandat
in antifaza pe intrarile de date S=d si ![]() ,
,
deoarece cand T=1 iesirea portii 1 este D. Simbolul bistabilului D este cel din figura 12f . In literatura tipul de bistabil D din figura 12d se mai numeste si bistabil lateh (zavor).
Bistabilul de tip T(provine de
la TOOGLE - comutator) nu este disponibil ca atare dar poate fi realizat prin
intermediul altor tipuri de bistabili. Bistabilul T asincron (figura 12g) se obtine comutand
impreuna intrarile de date J si K si obtinand astfel intrarea de
date T'. Conform tablei de adevar din figura 12b pentru T'=0, bistabilul
isi mentine starea Qn+1=Qn, iar pentru T'=1,
bistabilul comuta ![]() . Varianta sincrona a bistabilului T obtinut din
bistabilul JK sincron este reprezentata in figura 12h.
. Varianta sincrona a bistabilului T obtinut din
bistabilul JK sincron este reprezentata in figura 12h.
Bistabilul T sincron comuta la aplicarea fiecarui impuls de tact aplicat la intrare. Bistabilul T este folosit in principal la realizarea numaratoarelor binare.
5. CIRCUITUL BASCULANT MONOSTABIL
Circuitul basculant monostabil (CBM) este caracterizat prin aceea ca una dintre starile de echilibru este stabila iar cealalta este cvasistabila .
Comutarea din starea stabila in cea cvasistabila se realizeaza doar la o comanda externa iar revenirea in starea stabila se face dupa o durata de timp determinata exclusiv de parametrii interni ai CBM.
O schema simpla de CBM (figura 13a) poate fi obtinuta din schema CBB reprezentata in figura 7a prin realizarea unui cuplaj capacitiv intre T1 si T2 si conectarea rezistentei RB2 intre baza lui T2 si sursa de alimentare cu rol de rezistenta de temporizare.
In figura 13b este prezentata schema, modificata topologic, a monostabilului prevazut cu intrare de comanda in baza lui T1. Starea stabila a schemei corespunde saturarii lui T2. Valoarea scazuta a tensiunii din colectorul lui T2 in saturatie asigura transmiterea prin RB1 in baza lui T1 a unei tensiuni suficient de mici ca acesta sa fie blocat.
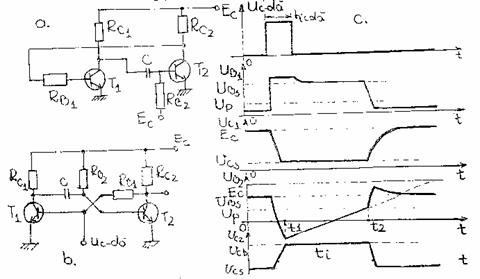
Fig. 13.
La aplicarea pe baza lui T1 a unui impuls pozitiv de comanda a carui durata sa indeplineasca conditia (19) acesta se deschide si declanseaza un proces tranzitoriu in avalansa care provoaca bascularea monostabilului in starea cvasistabila ( T1 in conductie, T2 blocat). Saltul negativ de tensiune din colectorul lui T1 aflat in conductie se transmite prin condensatorul C (acesta elimina componenta continua a tensiunii UC1) in baza lui T2 pe care il blocheaza. Starea cvasistabila dureaza atat timp cat tensiunea in baza lui T2 (care creste datorita incarcarii condensatorului C de la EC prin RB2 si prin tranzistorul T1 aflat in conductie la masa ) nu depaseste pragul UP de conductie. La atingerea acestui prag T2 se deschide si monostabilul revine un starea de avalansa in starea stabila initiala.( T1 blocat, T2.conductie). Saltul pozitiv de tensiune din colectorul lui T1 aflat in blocare se transmite prin C in baza lui T1 si determina o supra crestere a tensiunii UB2 la momentul t2 .Prin incarcarea condensatorului C de la EC prin RC1 si jonctiunea B-E a lui T1 aflat in conductie, tensiunea UB2 revine la valoarea de saturatie incipienta. Rezistenta de colector a tranzistorului T2 se determina din relatia 20:
![]()
Pentru ca, in starea stabila, T2
sa fie in saturatie, trebuie indeplinita conditia (15):
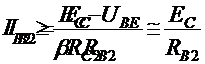
in care:
In final, conditia de saturatie
a lui T2 devine: ![]()

Rezistenta RB2 se
determina din (23) considerata la limita pentru a se asigura
functionarea in zona incipienta de saturatie.
Pentru ca in starea cvasistabila tranzistorul T1 sa fie in saturatie trebuie indeplinita conditia(15):
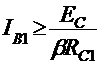
in care:
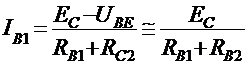
In final conditia de
saturatie a lui T2 devine:
![]()
Rezistenta RC1 din
colectorul lui T1 se determina tot din relatia (20). Diagramele
din figura (13c) arata ca CBM furnizeaza impulsuri cu durata data la
aplicarea unui impuls de comanda. Durata ti a impulsului de
iesire este proximatic egala cu intervalul de timp t2-t1.
De incarcare a condensatorului C cu constanta de timp
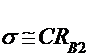
(incarcarea lui C este intrerupta de
deschiderea lui T2)
Folosind relatia (8) rezulta:
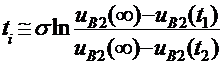
unde:
![]()
Durata aproximativa a impulsului
format de monostabil:
![]()
Depinde
deci exclusiv de circuitul temporizare format din C si RB2.
Amplitudinea impulsului din colectorul tranzistorului T1 este
![]()
deoarece curentul de colector ICb
al lui T1 aflat in blocare si tensiunea in colector la
saturatie UCS sunt
neglijabile.
Amplitudinea impulsului din colectorul T2 este:
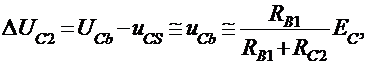
unde s-au neglijat pe rand tensiunea
din colectorul lui T2 la saturatie si tensiunea din baza lui T1
la blocare, desi amplitudinea este putin mai mica decat in colectorul
lui T1 cu semnal de iesire al CBM se prefera impulsul din
colectorul lui T2 deoarece are timpi de comutatie mai
redusi. Aceasta se datoreaza formei tensiunii din baza uB2
si prezinta un salt negativ puternic care reduce tCi si o
crestere pozitiva ce depaseste uBS care reduce tcd
.
Circuitul monostabil este utilizat ca formator de impulsuri cu durata data, ca circuit de intarziere al impulsurilor pe un interval de timp dat sau realizarea modulatiei in durata a impulsurilor.
Functionarea normala a CBM din figura 13b impulsul ca durata impusului de comanda sa fie mai mica decat durata impulsului format de monostabil (tcda<ti) in caz contrar impulsul de comanda se aplica in baza lui prin intermediul unui circuit de diferentiere RC (figura 4)
Circuitele basculante monostabile pot fi obtinute si prin folosirea portilor logice realizate in tehnologie integrata. In figura 14b sunt redate diagramele de timp corespunzatoare unui CBM realizat cu doua porti SI (figura 14a)
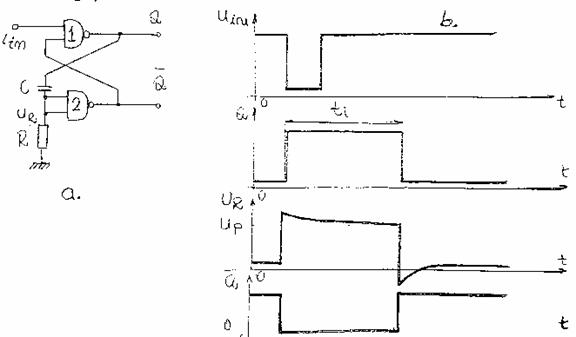
Fig. 1
Starea stabila a CBM este caracterizata prin uin=1,Q=0, Q=1,uR=0 iar condensatorul C este descarcat. La trecerea tensiunii de intrare in O conform tabelului de adevar din figura 9d, iesirea portii 1 este fortata in 1, saltul pozitiv de tensiune se aplica prin C la intrarile aflate in scurtcircuit ale portii 2 a carei iesire devine 0.Se produce astfel trecerea in avalansa a CBM in stare cvasistabila ( Q=1, Q=0). Pe masura ce condensatorul C se incarca prin rezistenta R la masa, tensiune uR scade si in momentul in care aceasta scade sub nivelul de prag up. Schema basculeaza in starea stabila (poarta 2 este fortata in 1 iar porta 1 cu ambele intrari in 1 revine in 0). Starea stabila initiala a CBM (Q=0)este asigurata daca tensiunea uR de pe rezistenta de temporizare, datorata curentului de la cele 2 intrari ale portii 2, este mai mica decat tensiunea de prag up .Daca portile SI-NU sunt realizate in tehnologie TTL (figura 6.17) tensiunea de prag este up=1,4V si rezulta:
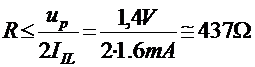
unde IIL este curentul
debitat de intrare a portii la care tensiunea este 0.
Durata ti a impulsului format de monostabil este proportionala cu constanta de timp de incarcare a condensatorului si asa cum se arata in lucrarea 9 este data de relatia:
![]()
Cele 2 relatii de mai sus
permit dimensionarea rezistentei si capacitatii de temporizare pentru
monostabilul cu porti TTL.
6. CIRCUITL BASCULANT ASTABIL
Circuitul basculant astabil (CBA) sau pe scurt astabilul este caracterizat prin faptul ca ambele stari de echilibru sunt cvasistabile. Duratele celor 2 stari cvasistabile sunt determinate exclusiv de parametrii circuitelor de temporizare RC din structura CBA. O schema cvasistabila larg folosita in practica este cea din fig. 15. a, care se obtine din schema CBM (fig. 13.) prin inlocuirea cuplajului rezistiv dintre colectorul lui T2 si baza lui T1 cu un cuplaj capacitiv. Diagramele de timp corespunzatoare sunt cele din figura 15,b.
S-a considerat ca astabilul se gaseste in starea (T1-blocat si T2-conductie), caz in care C1 se incarca prin RB1 si T2 pana cand tensiunea in baza lui T1 depaseste tensiunea de prag. In acest moment T1 intra in conductie, saltul negativ de tensiune din colectorul sau se transmite prin RC2 in baza lui T2 pe care il blocheaza si schema comuta in regim de avalansa in starea cvasistabila (T1-conductie, T2-blocat). Durata acestei stari este proportionala cu constanta de timp de incarcare a lui C2 prin RB2 si T1 si conform (25) rezulta:
ti1 ≈ 0,7 C2 RB2
Cand tensiunea pe baza lui T2 depaseste UP aceasta intra in conductie si provoaca blocarea lui T1. Astfel CBA revine in starea cvasistabila anterioara a carei durata este:
ti2 ≈ 0,7 C1 RB1
si procesul se repeta.
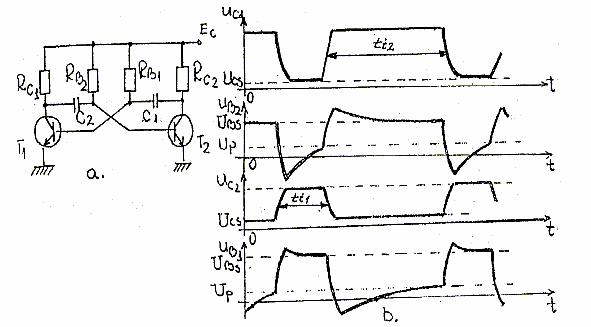
Fig.15
Rezistentele de colector RC1 si RC2 se determina folosind relatia (20).Intrarea in saturatie tranzistoarelor T1 si T2 necesita respectarea unor conditii similare cu (23) si anume:
RB1 ≤ ΒrC1 ; RB2 ≤ ΒrC2
Circuitele basculante astabile se folosesc ca generatoare de impulsuri dreptunghiulare cu durata data (ti1 sau ti2) si perioada de repetitie de asemenea data Tגּ ≈ 0,7 (C1 RB1 + C2RB2) .
O schema logica utilizata de astabil cu porti logice NU, realizate in tehnologie integrata, este cea din fig. 16 b.
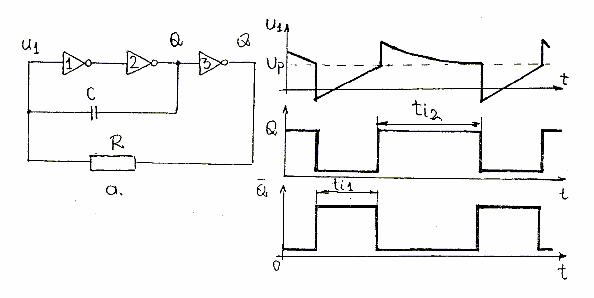
Fig.16
Portile logice NU sant in esenta amplificatoare de impulsuri inversoare.
Initial, starea CBA este: Q=1 , Q=1 si condensatorul C in curs de descarcare. In momentul in care u1 scade sub valoarea de prag poarta 1 este fortata in 1 conform tabelului de adevar din fig. 9. a. iar poarta 2 comuta in Q=0 fortand poarta 3 in Q=1. CBA a trecut deci in starea cvasistabila( Q=0 , Q=1) iar condensatorul C se incarca pe urmatorul traseu:iesirea portii3,condensatorul R,intrarea portii 2 (poarta aflata in 0 debiteaza curent iar poarta aflata in 1 absoarbe curent).
Durata starii cvasistabile est proportionala cu constanta de timp T=RC si asa cum se arata in lucrarea bibliografica [12], in cazul in care portile NU sunt de tip TTL este adevarata relatia: Ti1 ≈ 0,93RC
La atingerea pragului UP = 1,4 V ,astabilul comuta in . . (Q=1 , Q=0) iar condensatorul C se descarca pe acelasi traseu dar pe sens contrar.
Se demonstreaza ca durata acestei stari este:
Ti2 ≈ 3,2 RC
Pentru a se asigura un curent de comanda suficient de mare pentru poarta1 se impune ca:
R ≤ 1,8 KΩ
Astabilul din fig. 16. contine un singur circuit RC de polarizare. Din aceasta cauza rapoartele dintre duratele impulsurilor generate (ti1 sau ti2) si perioada de repetitie Tגּ = . + ti2 = 2,73 RC sunt constante.
Singura data de proiectare pentru CBA cu porti SI - NU e deci perioada de repetitie a impulsurilor generate
Astabilul din fig. 16.
contine un singur circuit RC de vaporizare. Din aceasta cauza
rapoartele dintre duratele impulsurilor generate (ti1 sau ti2)
si perioada de repetitie ![]() sunt constante.
sunt constante.
Singura data de proiectare pentru CBA cu porti SI - NU e deci perioada de repetitie a impulsurilor generate.
Un circuit basculant care poate functiona atat in regim astabil cat si in regim de monostabil este generatorul (GA) numit si uneori blocking. Se caracterizeaza prin aceea ca are in compunere un singur etaj de amplificare inversor cu transistor, prevazut cu o bucla de reactie pozitiva utilizata cu ajutorul unui transformator de impulsuri cu miez nesaturat. Generatorul autoblocat se utilizeaza in special pentru generarea (in regim de astabil) sau formarea (in regim de monostabil) a unor impulsuri de putere, cu durata foarte scurta si avand timpii de crestere si respectiv descrestere mici.
Cu titlul informative in fig. 71 a,b se prezinta schema, respective diagramele de timp ale GA in regim monostabil.
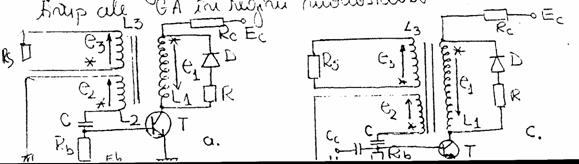
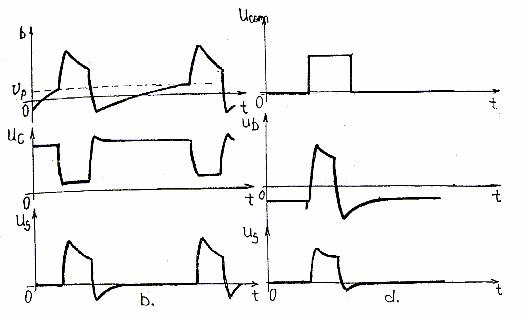
Fig.71
In fig. 17. a,c s-au notat cu asterix bornele bobinelor ale caror potentiale sunt in faza.
Se considera ca starea
initiala a GA in regim de astabil este cea in care T este blocat, iar
C se descarca. In momentul in care tensiunea in baza lui T
depaseste valoarea de prag, T intra in conductie
si schema comuta in regim de avalansa in noua stare
cvasistabila in care T este saturat (deschiderea lui T determina
scaderea tensiunii sale in colector care se transmite in
infasurarea L2 ca o crestere de tensiune, ceea ce il
deschide si mai mult pe T, etc.). Dupa comutare, in
infasurarea L2 se induce o tensiune electromotoare ![]() , datorita curentului crescator de magnetizare din
infasurarea L1. Condensatorul C se incarca de la e2
in principal prin rezistenta jonctiunii B-E a lui T la masa
si tensiunea in baza, UB=e2-UC scade
lent. In momentul in care T iese din saturatie, se stabileste bucla
de reactie pozitiva si GA comuta in avalansa in
starea cvasistabila initiala si T se blocheaza
(scaderea tensiunii in baza determina un salt pozitiv al
tensiunii in colector, care prin L2 se transmite ca salt negativ in
baza, tensiunea in colector creste si mai mult, etc.). Dioda D
si rezistenta R sunt destinate sa elimine oscilatiile
postimpuls care apar datorita excitarii circuitului format din L1
si capacitatea parazita Cp, de curentul de demagnetizare
Pe cat T este blocat,
, datorita curentului crescator de magnetizare din
infasurarea L1. Condensatorul C se incarca de la e2
in principal prin rezistenta jonctiunii B-E a lui T la masa
si tensiunea in baza, UB=e2-UC scade
lent. In momentul in care T iese din saturatie, se stabileste bucla
de reactie pozitiva si GA comuta in avalansa in
starea cvasistabila initiala si T se blocheaza
(scaderea tensiunii in baza determina un salt pozitiv al
tensiunii in colector, care prin L2 se transmite ca salt negativ in
baza, tensiunea in colector creste si mai mult, etc.). Dioda D
si rezistenta R sunt destinate sa elimine oscilatiile
postimpuls care apar datorita excitarii circuitului format din L1
si capacitatea parazita Cp, de curentul de demagnetizare
Pe cat T este blocat, ![]() si C se
descarca de pe armatura pozitiva prin L2, masa,
Eb, Rb la armatura incarcata negativ
astfel ca in baza lui T se aplica o tensiune negativa tot mai
mica pe masura ce condensatorul C se descarca. In momentul
in care tensiunea pozitiva Eb si tensiunea negativa
descrescatoare determina in baza o tensiune pozitiva mai
mare ca Up, GA comuta si incepe alt ciclu de
functionare. Generatorul autoblocat in regim de astabil genereaza
impulsuri dreptunghiulare cu durata foarte mica (zeci de ms pana la
μs) si perioada de repetitie cu cel putin doua ordine
de marime mai mare. Acestea sunt culese de infasurarea L3 de
cuplaj cu sarcina transformatorului de impulsuri.
si C se
descarca de pe armatura pozitiva prin L2, masa,
Eb, Rb la armatura incarcata negativ
astfel ca in baza lui T se aplica o tensiune negativa tot mai
mica pe masura ce condensatorul C se descarca. In momentul
in care tensiunea pozitiva Eb si tensiunea negativa
descrescatoare determina in baza o tensiune pozitiva mai
mare ca Up, GA comuta si incepe alt ciclu de
functionare. Generatorul autoblocat in regim de astabil genereaza
impulsuri dreptunghiulare cu durata foarte mica (zeci de ms pana la
μs) si perioada de repetitie cu cel putin doua ordine
de marime mai mare. Acestea sunt culese de infasurarea L3 de
cuplaj cu sarcina transformatorului de impulsuri.
In regim de monostabil, starea stabila a GA e asigurata de sursa Eb care polarizeaza negativ baza lui T, pe care il mentine blocat.
Pentru declansare, prin condensatorul de cuplaj CC se aplica un impuls pozitiv in baza lui T care se deschide si GA comuta in regim de avalansa in starea cvasistabila. Aceasta dureaza pana cand tensiunea in baza scade sub UP si GA revine in starea stabila. Generatorul autoblocat ca CBM formeaza impulsuri de scurta durata, mult mai mica decat durata impulsurilor de comanda.
7. Circuite de tensiune liniar variabila
Circuitele de tensiune liniar variabila (CTLV) reprezinta o categorie de circuite comutatie care genereaza sau formeaza impulsuri triunghiulare sau trapezoidale.
Generatoarele de tensiune liniar variabila (GTLV)realizeaza aceasta fara nici un semnal de comanda exterior iar formatoarele de tensiune liniar variabila (FTLV) folosesc in general impulsuri dreptunghiulare ca semnale de comanda.
Circuitele de tensiune liniar variabila se folosesc in sisteme de afisare cu tub catodic, in sistemele de masura numerice la conversia analog-numerica, in tesle-comanda, etc.
Ele mai sunt denumite si circuite de impulsuri in dinte de fierastrau sau circuite baza de timp.
Principalii parametrii ai tensiunii liniar variabile (TLV) sunt ilustrati in fig. 81.
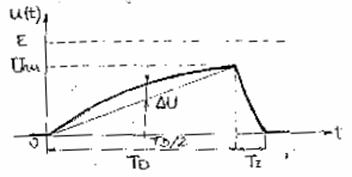
Fig.18
Amplitudinea Unu reprezinta valoarea maxima a tensiunii liniar variabile iar E este tensiunea de alimentare a CTLV.
Durata cursei directe TD reprezinta intervalul de timp in care TLV creste de la valoarea minima (de obicei nula), la Um, iar durata cursei inverse TI este intervalul in care aceasta revine la valoarea minima.
Marimea ΔU, numita abatere de neliniaritate reprezinta diferenta maxima dintre tensiunea liniar variabila ideala si cea reala.
Coeficientul de neliniaritate se noteaza si reprezinta abaterea relativa de neliniaritate:
![]()
Mai este definit si un coeficient de utilizare al tensiunii de alimentare prin relatia:
![]()
In cele mai multe cazuri, tensiunea liniar variabila se obtine prin incarcarea si respectiv descarcarea a unui condensator.
Conform (10.), pe durata cursei directe tensiunea pe condensator este:
![]()
unde ![]() este constanta de timp
de incarcare iar E tensiunea de alimentare. In lucrarea [9] se arata
ca in acest caz abaterea maxima
este constanta de timp
de incarcare iar E tensiunea de alimentare. In lucrarea [9] se arata
ca in acest caz abaterea maxima ![]() U fata de TLV ideala se obtine la
jumatatea duratei cursei directe iar coeficientul de neliniaritate si
coeficientul de utilizare a tensiunii de alimentare sunt legate prin
relatia:
U fata de TLV ideala se obtine la
jumatatea duratei cursei directe iar coeficientul de neliniaritate si
coeficientul de utilizare a tensiunii de alimentare sunt legate prin
relatia:
![]()
Cel mai simplu circuit de formare a tensiunii liniar variabile (FTLV) este format dintr-un circuit de comutatie cu tranzistor si comutator electric conectat in paralel cu un condensator (fig. 19. a).
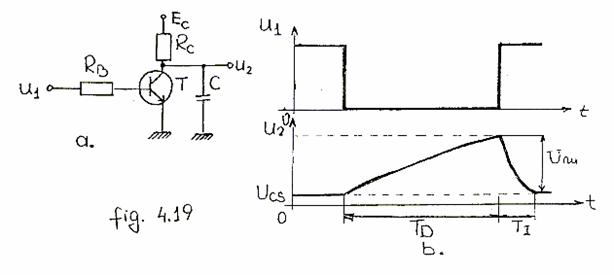
In starea initiala tensiunea u1 in baza este suficient de mare ca T sa fie saturat caz in care condensatorul C este descarcat. La aplicarea saltului negativ din baza, tranzistorul T se blocheaza si C se incarca de la EC prin RC la masa. Constanta de timp de incarcare este:
![]() » TD
» TD
La terminarea impulsului negativ din baza, tranzistorul T intra din nou in saturatie si C se descarca prin rezistenta C - E a lui T la masa cu constanta de timp:
![]() = rCES
= rCES ![]() « TD
« TD
Atunci cand T este blocat si C se incarca, tensiunea din colector este:
![]()
deoarece rezistenta C - E a lui T aflat in blocare este mult mai mare decat RC.
Deoarece in comparatie cu EC, tensiunea de colector la saturatie UCS este neglijabila conform (26) se poate considera ca amplitudinea tensiunii liniar variabile este:
![]()
Performantele FTLV din fig. 19
a sunt modeste. Pentru a imbunatatii liniaritatea tensiunii de
iesire este necesara cresterea constantei de timp de
incarcare ![]() (cresterea lui C
caci RC se determina insa scaderea amplitudinii
Unu a tensiunii de iesire
(cresterea lui C
caci RC se determina insa scaderea amplitudinii
Unu a tensiunii de iesire
Cresterea calitatii TLV se poate obtine daca se pastreaza un curent constant de incarcare pe toata durata TD a cursei directe, caz in care:
![]() ; i(t) = I
; i(t) = I
In cazul FTLV din fig. 20 a. s-a introdus un generator de curent constant realizat cu tranzistorul T2 de tip pnp cu baza la masa si emitatorul conectat la EC prin RE.
Daca Ec stabilizata atunci tensiunea B - E a lui T2 este constanta iar curentul sau de colector este de asemenea constant.
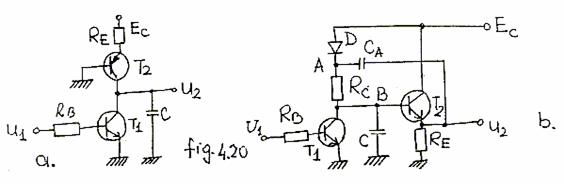
O alta modalitate de crestere a tensiunii TLV este aratata de schema din fig. 20 b. care foloseste in plus un repetor pe emitator realizat cu T2 si care prezinta o bucla de reactie pozitiva prin CA
La momentul initial tensiunea de comanda u1 (fig. 19 b.) asigura functionarea in saturatie a lui T1, C este descarcat, T2 este blocat, iar condensatorul de acumulare CA este incarcat aproape de EC. Impulsul negativ din baza il blocheaza pe T1 si condensatorul C se incarca de la EC prin dioda D aflata in conductie si prin RC la masa,tensiunea la intrarea lui T2 creste si acesta se deschide.
Potentialul punctului A este dat de relatia:
UA = UCA + U2
unde UCA este apropiat de EC. De aceea la deschiderea lui T2 tensiunea U2, aproximativ egala cu potentialul punctului B, creste si dioda D se blocheaza. Condensatorul C continua incarcarea pe seama sarcinii acumulate de condensatorul CA (deoarece CA » C sarcina acumulata este suficient de mare ca pe durata incarcarii lui C, tensiunea UCA sa fie practic constanta). Rezulta ca potentialul punctului A va urmari cresterea potentialului punctului B pe durata incarcarii condensatorului C.
UA=UCA + U2 ≈ UCA + UB; UCA ≈ ct.
Diferenta de potential la bornele rezistentei RC este UA - UB = UCA ≈ct. si curentul ce strabate rezistenta, egal practic cu curentul de incarcare a lui C, se va mentine constant.
La terminarea impulsului negativ de comanda, T1 se deschide si C se descarca, tensiunea UB scade pana cand T2 se inchide, dioda d se deschide si condensatorul CA care s-a descarcat intr-o mica masura pe durata cursei directe se incarca la nivelul initial de la EC prin D si prin RE la masa.
Repertoriul de tensiune realizat cu T2 asigura practic incarcarea cu un curent constant a lui C datorita amplificarii unitare in tensiune din care cauza U2 ≈ UB. In plus acesta prezinta avantajul unei rezistente de intrare mare prin care se evita scurtcircuitarea condensatorului C pe durata incarcarii.
Copyright © 2024 - Toate drepturile rezervate