Istoric despre aparitia si evolutia chitarei in timp

MOTTO :

Muzica ne da ceea ce cerul si pamantul ne refuza « 

Introducere

Lucrarea de fata contine un scurt istoric despre aparitia si evolutia chitarei in timp, un material informativ despre cum putem realiza singuri acordarea propriei chitare si un material stiintific despre cum se calculeaza si se plaseaza barele pe tastiera unei chitare.

Acest referat este special conceput pentru elevii care isi indreapta atentia spre scoli si licee de arta, nu pentru ca ar avea vreun talent artistic sau pentru ca le-ar placea pictura, sculptura sau muzica, ci pentru ca in acest scop ar putea scapa de matematica.

Le recomandam acestora si tuturor celor care cred ca matematica nu are nimic in comun cu muzica sa citeasca cu atentie acest proiect. Vor fi surprinsi sa afle ca matematica sta la baza asezarii barelor pe tastiera unei chitare, obtinerea unor note pe anumite coarde facandu-se printr-un calcul matematic.

Speram ca proiectul nostru sa capteze atentia si interesul cat mai multor persoane!

1. Scurt istoric

Muzica se naste prin intermediul a trei elemente: repertoriu, instrument si interpret; pentru ca o lucrare muzicala nu prinde viata decat atunci cand notele care mai inainte erau asezate pe partitura, se aud dintr-un instrument care vibreaza alaturi de cel care il manuie.

In spiritul acestei idei, cand vorbim despre evolutia istorica a unui instrument, vorbim despre evolutia acestor trei elemente mentionate mai sus. De cele mai multe ori repertoriul declanseaza procesul de transformare a instrumentelor; de exemplu piesele muzicale cu o polifonie complexa cer instrumente capabile sa ofere claritate, volum mare care sa faciliteze evidentierea vocilor la nivele diferite de intensitate, cat si o tehnica de interpretare din ce in ce mai buna. Nu putine sunt situatiile in care anumite lucrari muzicale nu puteau fi abordate de interpretii din perioada in care au fost scrise.

Chitara s-a dezvoltat si ea sub aceste trei aspecte, ajungand in zilele noastre sa aiba un potential expresiv deosebit. Popularitatea acestui instrument, poate in mod paradoxal, il face sa fie subapreciat; numarul mare de chitaristi amatori creand senzatia de instrument usor de abordat, lipsit de complexitate.

Acordata standard, chitara se poate folosi ca instrument principal in toate stilurile muzicale, iar tehnica de chitara clasica o pune cel mai bine in valoare. Alte tipuri importante de tehnica aplicata la chitara sunt cele specifice stilului gypsy jazz, sau swing, stil ce il are ca reprezentant pe chitaristul Django Reindhardt, aici sunt puse in valoare functiile percusive ale chitarei printr-o serie de tehnici specifice, si cea folosita la chitara electrica.

Instrumente care se aseamana cu chitara apar cu foarte mult timp in urma, cu cca.5000 ani. Prima chitara cu sase corzi a aparut in Spania ca rezultat al unui proces indelungat de evolutie. O reprezentare in piatra, veche de 3.300 de ani infatiseaza un bard cantand la un instrument ce intalneste caracteristicile cele mai importante ale chitarei. Primele instrumente cu coarde, ce aveau o asa-zisa tastiera, apar inca din epoca antica. Foloseau corzi confectionate din intestine de animale.

Ca precursori ai chitarei amintim: chitara renascentista, lauta, mandora. Chitara moderna are ca stramos indepartat chitara romana. In secolele XV-XVI apare un instrument: "viola da mano", considerat stramosul imediat al chitarei moderne, asemanandu-se ca mod de acordare cu lauta si avand structura cutiei de rezonanta asemanatoare cu cea a chitarei moderne.

Din repertoriul acestui instrument fac parte lucrari ale compozitorilor: Luis de Milán (1536), Luis de Narváez (1538), Enríquez de Valderrábano. Se considera ca prima chitara moderna a fost facuta de lutierul italian Gaetano Vinaccia in anul 1779. Dimensiunile chitarei clasice, sau spaniole cum mai este numita, au fost stabilite de Antonio Torrez Jurado in jurul anului 1850 in Sevilia.

De atunci chitara a avut parte de numeroase imbunatatiri, iar procesul de evolutie e departe de a se fi terminat; lutierii contemporani continuand sa modifice structura instrumentului (apar instrumente cu mai multe orificii, cum sunt chitarele "La Mancha"). Repertoriul actual al chitarei clasice este unul deosebit de bogat, intins pe toate genurile muzicii culte, au fost facute transcriptii ale lucrarilor celor mai importanti compozitori si pe langa acestea exista desigur un numar mare de piese scrise pentru chitara.

Printre cei mai importanti compozitori ii amintim pe Augustin Barrios Mangore, Fracisco Tarrega, Jaquin Rodrigo, Rolan Dyens, Leo Brouwer, Heitor Villa Lobos, Mauro Giuliani, samd.

In clipa in care un artist interpreteaza o piesa la chitara, trebuie sa mareasca valoarea de existenta a lumii descrise de piesa, pentru ca in felul acesta sa-i faca pe oameni sa "fie acolo".

Iar dupa cum spunea Beetoven, daca vrei sa-i emotionezi pe ceilalti trebuie ca tu insuti sa fi emotionat. Chitara este pentru interpreti, calea catre lumea de dincolo de noi, lume care ne face cu adevarat oameni.

2. Acordarea unei chitare

Cea mai simpla metoda de acordare a unei chitare este folosirea unui acordor electronic sau a unui program de acordare.

Acum o sa prezentam metoda clasica de acordare a unei chitare.

Acordajul standard pentru o chitara cu 6 corzi este urmatorul:

Pentru a acorda chitara aveti nevoie de un camerton sau de un diapazon sau in caz ca nu aveti nici unul dintre acestea doua, este bun chiar si 'tonul de telefon'.

Camertonul - este un instrument folosit pentru acordat, construit din tuburi cu gauri (se gaseste la majoritatea magazinelor de muzica la fel ca si diapazonul). Exista camerton cu 4 tuburi si cu 6 tuburi. Pentru acordajul chitarei se foloseste cel cu 6 tuburi. Fiecare tub prin care se sufla da o frecventa specifica unei note.

Diapazonul - este un alt instrument pentru acordat. El vibreaza la frecventa care da nota folosita in limbajul muzical international , LA.

Daca avem camerton , se sufla in primul tub care da nota MI . Se intinde prima coarda MI (1) pana suna la unison cu camertonul. Se sufla in al doilea tub care da nota SI . Se intinde a doua coarda SI pana suna la unison cu camertonul. In acest fel se sufla pe rand in fiecare tub corespunzator coardei cu care trebuie sa sune la unison. Reglajul se face din chei.

Daca avem diapazon acordajul se face astfel:

Coarda MI (1) - Diapazonul se loveste de un obiect si se pune bratul mai lung pe cutia de rezonanta a chitarei. Datorita rezonantei se aude sunetul LA. Pastram sunetul in memorie. Imediat punem degetul aratator de la mana stanga pe prima coarda MI (cea subtire), in pozitia 5 (tastiera 5) si apasam. Cu degetul mare de la mana dreapta ciupim coarda.

Cu ajutorul cheilor reglam coarda pana suna la unison cu diapazonul. Efectuam aceasta operatiune (lovirea diapazonului - ciupirea coardei - reglajul cu cheia) de cate ori este nevoie. Astfel se acordeaza coarda MI. Dupa ce am terminat de acordat prima coarda nu mai avem nevoie de diapazon.

Coarda SI (2) - Apasam in pozitia 5 (tastiera 5) cu ajutorul degetului mijlociu 2 de la mana stanga pe coarda SI . Cu degetul mare de la mana dreapta ciupim coarda MI (1) (libera, fara sa apasam in vreo pozitie). Memoram sunetul. Apoi imediat ciupim coarda SI (care este dinainte apasata cum am spus) tot cu degetul mare de la mana dreapta. Reglam cu ajutorul cheii coarda SI pana cand suna la unison cu prima, obtinand sunetul MI. Efectuam aceasta operatiune de cate ori este nevoie.

Coarda Sol (3) - Apasam cu indexul pe coarda 3 in pozitia 4. Cu degetul mare de la mana dreapta lovim coarda SI (2) (libera). Memoram sunetul. Apoi imediat lovim coarda 3 care deja este apasata. Reglam cu ajutorul cheii coarda Sol pana cand suna la unison cu coarda SI (2).

Coarda RE (4) - Apasam cu indexul coarda 4 in pozitia 5. Lovim coarda Sol (3) (libera). Memoram sunetul. Apoi imediat lovim coarda 4. Reglam cu ajutorul cheii coarda Re (4) pana cand suna la unison cu coarda Sol (3).

Coarda LA (5) - Apasam cu indexul coarda 5 in pozitia 5. Lovim coarda RE (4) (libera). Memoram sunetul. Apoi imediat lovim coarda 5. Reglam cu ajutorul cheii coarda LA (5) pana cand suna la unison cu coarda RE (4).

Coarda MI (6) - Apasam cu indexul coarda 6 in pozitia 5. Lovim coarda LA (5) (libera). Memoram sunetul. Apoi imediat lovim coarda 6. Reglam cu ajutorul cheii coarda MI (6) pana cand suna la unison cu coarda LA (5).

Daca avem doar un telefon cu ton.

Tonul telefonului reprezinta de fapt nota LA. Tot ce avem de facut este sa acordam coarda MI (1) a chitarei noastre. Acest lucru se face ca si cu diapazonul, singura diferenta fiind ca nota LA ne este data acum de tonul telefonului. Urmam astfel toate instructiunile de la acordajul cu diapazonul.

3. Tratarea stiintifica a temei

"Plasarea barelor pe tastiera unei chitare "

Muzicologul J. M. Barbour a prezentat o discutie remarcabila privitoare la plasarea barelor unei chitare, dupa sistemul cu temperaj egal, printr-o constructie geometrica aproximativa datorata muzicologului suedez D. P. Strähle (1743).

Autorul a fost referent pentru articolul lui Barbour contribuind la acesta cu doua scurte note infra, care aveau scopul sa simplifice analiza lui Barbour. Ele stau la baza prezentei teme.

Pentru a putea introduce subiectul nostru, vom trata mai intai metoda de acordare a instrumentelor cu claviatura, cunoscuta ca temperaj egal (T.E).

3.1. Scara muzicala cu temperaj egal

O nota muzicala are o frecventa , care este numarul oscilatiilor complete pe secunda ale unei coarde care o produce. Daca doua note si de frecventa si sunt auzite simultan, efectul dublei note asupra urechii depinde, in principal, de raportul . Vorbim de un interval consonant sau de o consonanta, daca raportul acesta, scris cu termenii cei mai simpli, este

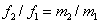, (3.1.1)

unde si sunt intregi mici; acest fapt a fost cunoscut inca vechilor greci. Cu exceptia unisonului, cand , avem cel mai important caz, cand , , producand octava.

Pentru a descrie celelalte consonante, ne trebuie notele scarii cromatice, ale octavei de la la , notate ca de obicei prin

. (3.1.2)

In notatia literala, notelecorespund notelor Do, Re, Mi, Fa, Sol, La, Si, Do.

In tabelul 1 se dau intervalele consonante cu numele lor si raportul frecventelor, determinate prin experiente cu monocorzi.

Aceste experiente au fost posibile, datorita operei lui Marin Mersenne (1588 - 1648), un coleg si prieten al lui Descartes. El a descoperit ca o coarda uniforma, intinsa, de lungime are o frecventa data de

, (3.1.3)

unde este o constanta care depinde numai de densitatea liniara si de tensiunea coardei.

Tabelul 1

Intervale consonante

Ne referim la tratatul lui Rayleigh [6, p. 8 - 9] , unde el deduce din tabelul 1, frecventele notelor din gama major. Luand frecventa lui drept unitate, aceste frecvente, scrise sub notele corespunzatoare sunt: (3.1.4)

Aceasta este asa-zisa scara diatonica major. Aceasta acordare poate fi continuata de-a lungul intregii claviaturi prin octave succesive. Acordarea astfel obtinuta pare satisfacatoare atata timp cat se face muzica numai in major, dar apar dificultati de indata ce executantul incearca sa moduleze. Ca un exemplu, cvinta cu baza in este intervalul . Din (3.1.4) se gaseste ca raportul frecventelor ei este:

(5/3) / (9/8) = 40/27 = 1,48148.

Aceasta difera de raportul teoretic cu 0,01852, fiind o eroare relativa de , care este inacceptabila.

Solutia acestor dificultati a condus, incepand din secolul al XV-lea, la acordarea instrumentelor cu claviatura, dupa asa-zisul sistem cu temperaj egal (T.E.). Scara cromatica a T.E. este bazata pe conditia: raportul frecventelor intre doua note consecutive din (3.1.2) sa fie constant.

Cum in (3.1.2) avem douasprezece astfel de intervale, numite semitonuri, si cum dorim ca , urmeaza ca pentru fiecare semiton sa avem raportul:

. (3.1.5)

Aceasta conditie, de importanta capitala, atribuie notelor din (3.1.2) frecvente date in tabelul 2, unde . Tabelul 2 arata frecventele T.E.

A treia coloana repeta frecventele diatonice din (3.1.4) si le compara cu cele din T.E. Ultima coloana prezinta erorile relative. De notat valorile mici ale acestora, valori pe care semenii nostri nu le-ar percepe; Mozart ar fi putut fi tulburat de erorile din si .

Acordarea cu progresia geometrica de ratie este continuata pe toata claviatura. Este un fapt fizic de mare importanta ca scara naturala, sau diatonica, este atat de bine aproximata de progresia geometrica din tabelul 2.

Tabelul 2

Frecvente T.E.

Ce face ca T.E. sa fie atat de important ?

Raspunsul este ca scara cromatica , este echivalenta din punct de vedere muzical cu scara in orice alta octava. Se poate canta la instrument in orice cheie dorita si modulatia este nelimitata.

J. S. Bach a fost un mare campion al T.E. Pentru a raspandi avantajele sale, el a publicat in 1722 " Clavecinul bine temperat ", continand 24 Preludii si Fugi in toate cheile majore si minore. Acestea pot fi executate cu un instrument cu claviatura acordat in T.E.

3.2. Plasarea aproximativa a barelor pe tastiera unei chitare dupa Strähle.

Reamintim rezultatul lui Mersenne din (3.1). O coarda uniform intinsa, de lungime are o frecventa de vibratie data de

, (3.2.1)

unde este o constanta care depinde de densitatea liniara si de tensiunea coardei. Fie OB coarda deschisa a chitarei care produce nota . Sa alegem OB, drept axa Oy, cu originea in O, astfel incat in punctul B. Fie A, mijlocul lui, unde .

Din (3.2.1) avem ca barele care produc scara cromatica de la la , trebuie plasate in 12 puncte cu abscisele:

, unde , (3.2.2)

cum sunt reprezentate in figura 1.

Aceasta este o progresie geometrica cu ratia In mod echivalent trebuie sa inseram, intre punctele si , unsprezece medii proportionale. Daca coarda deschisa OB da nota , notele obtinute fixand coarda la bare vor fi cele ale scarii cromatice din tabelul 2 din (3.1).

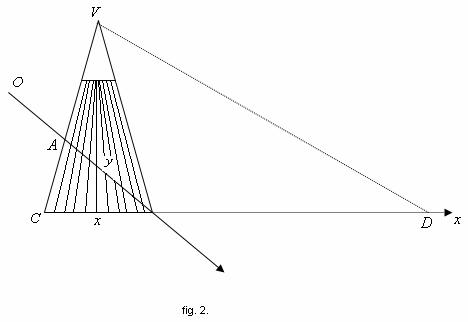
Constructia aproximativa a lui D. P. Strähle, reprezentata in figura 2, este urmatoarea:

Fie un triunghi isoscel cu laturile 24, 24 si 12 unitati. Sa marcam pe punctul , astfel incat unitati si apoi sa construim inaintea lui , astfel incat . Sa divizam baza in 12 parti egale si sa unim cele 12 puncte de diviziune, inclusiv , cu varful . Intersectiile dreptelor astfel obtinute cu sunt cele 12 puncte:

. (3.2.3)

Acestea sunt punctele de pe , unde trebuie plasate barele. Operatia prin care se uneste un punct, de pe , cu si se ia intersectia , a lui cu , se numeste o perspectivitate, fiind centrul perspectivitatii. Alegem ca axa , asa ca si sa corespunda punctelor si, respectiv. Analog, fie axa , asa ca , si sa corespunda punctelor , si .

Presupunem ca stim ca dependenta dintre si este de forma:

. (3.2.4)

Pentru motive evidente, aceasta este numita o functie liniara fractionara, careia urmeaza sa-i determinam coeficientii. Ducem paralel la (figura 2.) si fie intersectia cu . Prin triunghiuri asemenea gasim ca . Dar perspectivitatea arata ca valoarea corespunzatoare lui este si asta ne arata ca (3.2.4) trebuie sa fie de forma:

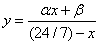. (3.2.5)

Mai mult, figura 2. arata ca pentru si , valorile corespunzatoare ale luisunt si . Aceasta ne da doua ecuatii liniare pentru si cu solutiile si . De aceea, forma finala a dependentei dintre si este:

, de unde . (3.2.6)

 

 

Coordonatele ale punctelor (3.2.3), unde trebuie plasate barele dupa Strähle, sunt:

(3.2.7)

in timp ce dupa E.T., (cum sunt date in figura 2.), ele sunt:

(3.2.8)

Aceasta conduce la intrebarea: Cat de bine aproximeaza pe

Un raspuns evident ar fi sa calculam valorile (3.2.7) si sa le comparam cu valorile (2.2.8) din tabelul 2. Este insa mai instructiv sa discutam o problema de interpolare preliminara.

3.3. Aproximarea unei functii exponentiale printr-una liniara fractionara.

Fie si date, ; sa consideram functia exponentiala crescatoare:

(3.3.1)

De notat ca , , . Sa aproximam pe in , printr-o functie liniara fractionara:

. (3.3.2)

Pentru a o obtine, folosim interpolarea; cum depinde de trei parametrii arbitrari, ii alegem asa ca sa interpoleze in cele trei puncte , si . E usor de verificat ca: 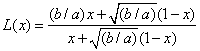. (3.3.3)

este functia interpolatoare cautata, pentru ca satisface ecuatiile:

, , . (3.3.4)

Daca raportul nu este prea mare, pare rezonabil sa ne asteptam ca definit de (3.3.3) sa fie destul de aproape de , in intervalul . Sa consideram cazul special care ne intereseaza. Daca si , deci , (3.3.5) atunci functia interpolatoare (3.3.3) devine:

(3.3.6)

unde utilizam litera B, de la Barbour, care a folosit aceasta functie interpolatoare. Pentru , unde ne asteptam la cea mai mare diferenta, gasim:

. (3.3.7)

Se vede ca ; aceasta este o eroare relativa de 0,13%, care din punct de vedere muzical este nesemnificativa. Deci functia lui Barbour (3.3.6) este o aproximatie acceptabila pentru .

Dar cat de buna este aproximatia lui Strähle (3.2.6) ?

Stim ca amandoua, si interpoleaza in si si ca ele trebuie sa difere in . Aceste valori sunt:

(3.3.8) si

(3.3.9)

Se vede o diferenta de 0,00043, care este cu totul insignifianta. De pe vremea lui Christian Huygens (1629 - 1695) se stie ca in aproximarea numerelor irationale prin rationale, putem utiliza redusele dezvoltarilor in fractii continue. Fractia continua a lui este:

,

redusele ei succesive fiind: (3.3.10)

Comparand numitorii in ultimele fractii din (3.3.8) si (3.3.9), vedem ca se poate obtine aproximatia lui Strähle din aproximatia lui Barbour prin inlocuirea in (3.3.8) a numitorului cu fractia , care e ultima redusa din (3.3.10).

Dupa o teorema fundamentala a lui Lagrange (1736 - 1813) se stie ca este cea mai buna aproximatie a lui printre toate fractiile rationale cu sau .

Cum a descoperit Strähle constructia sa, ramane un mister, pentru ca el nu avea cultura matematica. Trebuie sa fi fost intuitie, sprijinita pe mestesug. Contributia lui nu a fost apreciata la vremea ei, datorita unei erori numerice facute de un matematician contemporan, caruia i s-a cerut sa-i controleze lucrarea si care astfel a conchis ca nu este suficient de corecta. Barbour a descoperit greseala si a aratat valoarea ei.

Bibliografie

Grigore Constantinescu, Irina Boga, « O calatorie prin istoria muzicii « , Ed. Didacticǎ si Pedagogicǎ, Bucuresti

Isaac J. Schoenberg, « Privelisti matematice , Ed. Tehnica, Bucuresti 1989;

www.google.com