PROGRAMAREA IN MATHCAD - laborator

PROGRAMAREA IN MATHCAD

1. Calculul suprafetei unui poligon pe cale analitica (Math - Options - Array Origin=1):

Relatia de calcul utilizata pentru determinarea suprafetei unui poligon pe cale analitica, pornind de la coordonatele varfurilor sale este:

S2 = (1)

unde:

S2 reprezinta suprafata dubla a poligonului,

NV este numarul varfurilor sale,

X_i si Y_i sunt coordonatele fiecarui varf I.

Deoarece relatia de calcul este circulara, se impun urmatoarele precizari:

pentru I = 1, I 1 este NV (nu 0),

iar pentru I = NV, I 1 este 1 (nu NV

Algoritmul care trebuie parcurs pentru rezolvarea problemei contine urmatorii pasi:

Initializarea valorii S;

Calculul valorii S2 cu relatia (1), punand conditiile logice mentionate pentru I = 1 si I = NV;

Obtinerea suprafetei poligonului, S, cu semnul plus (poate iesi negativa din cauza jocului de coordonate si al sensului de parcurgere a poligonului);

Afisarea rezultatului obtinut.

Programul "suprafata_poligon" este limitat la poligoane cu 1 la 255 de varfuri (cei doi vectori X si Y au cate 256 pozitii, de la 0 la 255). Valorile I 1 si I 1 au fost inlocuite cu variabilele K si J.

2. Calculul distantei cumulate si a cotei cumulate prin nivelment trigonomtric:

Sa presupunem ca pe profilul longitudinal al unui tronson de drum sunt amplasati n picheti. Pentru fiecare dintre picheti ne propunem sa determinam distanta orizontala cumulata pana la acesta precum si cota fiecarui pichet pornind de la cota cunoscuta a primului pichet.

Datele de teren necesare rezolvarii problemei sunt:

distantele inclinate (di_i)  dintre doi picheti;

unghiurile verticale (uv_i), reprezentand inclinarea terenului intre doi picheti.

Pe teren s-au masurat unghiuri zenitale in gradatie centesimala. De aceea, unghiul vertical citit se corecteaza cu formula (2), dupa care se transforma in radiani cu relatia (3). 

uv_i = | uv_i - 200 | - 100  (2)

uv_i = (3)

Distanta cumulata (dc) se obtine prin insumarea distantelor dintre doi picheti (distante reduse la orizont - o_i), care, la randul sau, se calculeaza in functie de distanta inclinata (di_i) - relatiile (4) si (5):

o_i = di_i · cos² · uv_i  (4)

dc = (5)

Asemanator, cota cumulata (cc) se obtine prin insumarea diferentelor de cota (difc_i), care se calculeaza tot in functie de distanta inclinata - relatiile (6) si (7).

difc_i = o · (6)

cc = (7)

Programul "nivelment_trigonometric" debuteaza cu citirea numarului de picheti (n) si a cotei initiale (ci), apoi, intr-un ciclu realizat cu instructiunea for, realizeaza corectiile de rigoare, dupa care calculeaza distanta redusa la orizont si diferenta de nivel.

3. Sa se realizeze un program pentru determinarea orientarilor din coordonate:

Sa admitem ca, pornind de la coordonatele cunoscute ale unui numar de NP puncte, ne propunem sa determinam orientarea q_P-I dintre oricare doua puncte din cele date, P (X_P ,Y_P) si I (X_I ,Y_I).

Dupa cum se cunoaste, relatiile de calcul sunt diferentiate pe cadrane conform precizarilor din tabelul 1.

Pentru a utiliza intotdeauna relatia de calcul corespunzatoare cadranului in care se gaseste orientarea, trebuie precizat cadranul  prin compararea coordonatelor punctului I cu cele ale punctului P conform tabelului 1.

Relatiile pentru stabilirea formulei de calcul al orientarilor pe cadrane

Tabelul 1

Conditii de stabilire a cadranului

Tabelul 2

Algoritmul pe care trebuie sa-l parcurgem pentru rezolvarea problemei contine urmatorii pasi:

Citirea numarului de  puncte NP;

Introducerea numerelor  de identificare a doua puncte I si P intre care se dorestre a fi calculata orientarea (in program j si k);

Intr-un ciclu for se exprima relatiile de calcul a orientarii pentru fiecare cadran in parte;

Afisarea orientarii calculate;

Eventuala reluare a executiei pentru alte doua puncte (prin schimbarea valorilor pentru j si k).

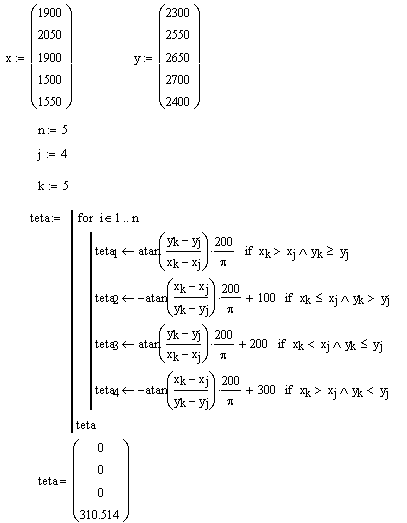
Programul "orientari" foloseste variabila "n" pentru numarul de puncte NP, iar pentru notatiile I si P foloseste variabilele "k" si "j".