TRIUNGHIUL LUI PASCAL

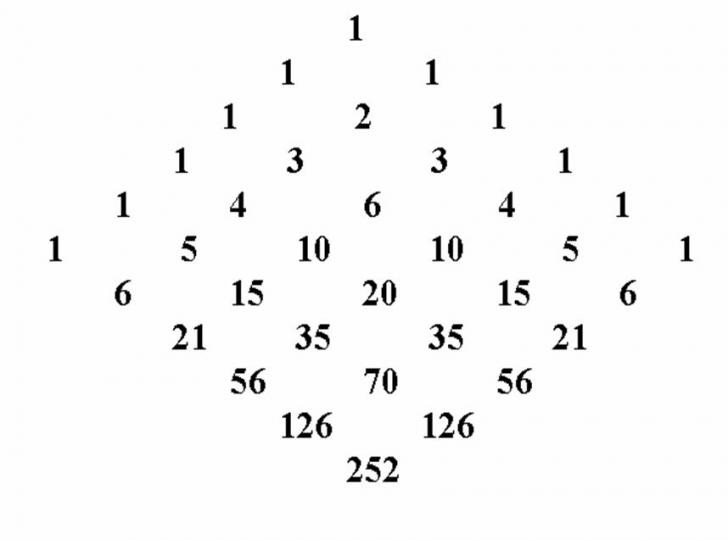
Numerele din figura (1) sunt coeficientii binomiali, iar dispunerea lor sub forma de tabel triunghiular se numeste triunghiul lui Pascal. Insusi Pascal numea acest triunghi     aritmetic.

Fig. (1)

La triunghiul din figura (1) pot fi adaugate noi linii, el poate fi extins oricat de mult.

Reteaua din figura (2) este de fapt, o portiune patrata "taiata" dintr-un triunghi mai mare.

Figura (2)

Unii dintre coeficientii binomiali si descompunerea lor intr-un tabel triunghiular apar si in scrierile altor autori, anterioare lucrarii lui Pascal. Meritele lui Pascal in aceasta descoperire sunt suficiente pentru a justifica utilizarea numelui lui.

In primul rand trebuie sa introducem o notatie pentru numerele continute in triunghiul lui Pascal. Pentru noi fiecare numar asociat unui punct din acest triunghi are o semnificatie geometrica: el indica numarul de trasee distincte, in zigzag, de lungime minima, de la varful triunghiului pana la punctul respectiv. Fiecare din aceste trasee trece de-a lungul unui aceluiasi numar de cvartale - sa spunem de-a lungul a n cvartale. Mai mult, toate aceste trasee concorda intre ele si in ceea ce priveste numarul de cvartale strabatute mergand spre sud-vest si numarul de cvartale strabatute mergand spre sud-est.

Fie l si respectiv r aceste numere (l -inseamna deplasari spre stanga, r - inseamna deplasari spre dreapta, bineinteles in fiecare caz directia generala este de sus in jos).

Evident: n=l+r.

Daca notam doua din cele trei numere n, l si r, al treilea este complet determinat, si tot asa este si punctul la care ele se refera.

Vom nota cu C^r_n (combinari de n luate cate r) numarul de trasee minime de la varful triunghiului lui Pascal pana la punctul specificat de numarul n (numarul total de cvartete) si numarul r (cvartetele strabatute mergand spre dreapta).

De exemplu in figura (3): C³₈=56; C⁵₁₀=252. Simbolurile pentru numerele din figura (1), au fost grupate in mod corespunzator in figura (3).

Simbolurile cu acelasi numar "inferior n" se aliniaza pe orizontala in lungul "bazei" de ordinul n, este vorba de baza unui triunghi dreptunghic.

Simbolurile cu acelasi numar "superior r" se aliniaza oblic in lungul "bulevardului" cu numarul r.

Figura (3)

In al doilea rand pe langa aspectul geometric, triunghiul lui Pascal prezinta si un aspect legat de proprietati numerice si de calcul. Toate numerele de-a lungul frontierelor (strada zero, bulevardul zero si punctul lor comun de plecare) sunt egale cu 1.

Prin urmare: C⁰_n=Cⁿ_n=1

Aceasta relatie se numeste conditia la limita a triunghiului lui Pascal.

Orice numar din interiorul triunghiului lui Pascal este situat pe un anumit rand orizontal, sau pe o anumita "baza". Un numar oarecare de pe baza (n+1) se calculeaza "mergand inapoi" sau "recurgand" la cele doua numere vecine de pe baza n:

C^r_n+1=C^r_n+C^r-1_n.

Aceasta formula se numeste formula de recurenta a triunghiului lui Pascal.

Din punctul de vedere al proprietatilor de calcul, numerele C^r_n sunt determinate de formula de recurenta si de conditia la limita a triunghiului lui Pascal.

Cand calculam un numar din triunghiul lui Pascal folosind formula de recurenta, trebuie sa ne bazam pe cunoasterea prealabila a doua numere de pe baza "precedenta". Exista insa o schema de calcul care este independenta de cunostintele prealabile si o vom numi formula explicita a coeficientilor binomiali:

Tratatul lui Pascal contine formula explicita, Pascal nu spune insa cum a descoperit-o dar in schimb da o demonstratie cu totul remarcabila a formulei explicite. In demonstratie Pascal utilizeaza doua leme, in prima lema arata ca formula explicita este valabila si pentru prima linie iar in cea de-a doua lema arata ca daca formula este valabila pentru o baza oarecare n, atunci ea este valabila si pentru baza imediat urmatoare (n+1).

Pascal spunea: "Vedem deci ca propozitia este, in mod necesar, valabila pentru toate valorile lui n. Caci ea este valabila pentru n=1, in virtutea primei leme, prin urmare ea este valabila si pentru n=2, in virtutea lemei a doua; prin urmare ea este valabila si pentru n=3, in virtutea aceleiasi leme si asa mai departe, ad infinitum."

Cuvintele lui Pascal citate aici au o importanta istorica, fiindca demonstratia data de el constituie primul exemplu de aplicare a unei scheme fundamentale de rationament, care se numeste in mod obisnuit: inductie matematica.

Pana acum am dat trei moduri distincte de abordare a numerelor din triunghiul lui Pascal:

interpretarea geometrica (un coeficient binomial este numarul de drumuri distincte minime, intre doua noduri ale unei retele de strazi);

abordarea formala (adica exclusiv prin calcul, coeficientii binomiali pot fi definiti prin formula lor de recurenta si prin conditia la limita);

formula explicita;

Denumirea numerelor ne mai aminteste o cale:

teorema binomului:

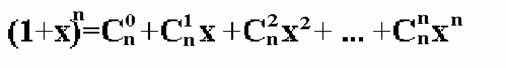Pentru orice x (fix sau variabil) si pentru orice intreg nenegativ n, are loc egalitatea:

Exista si alte moduri de a aborda numerele din triunghiul lui Pascal, numere ce joaca un rol important in foarte multe probleme interesante si se bucura de foarte multe proprietati interesante.

"Acest tabel de numere are proprietati eminente si admirabile" spunea Jaques Bernoulli, "in el sta esenta combinatoricii, iar cei familiarizati cu geometria stiu ca in el sunt ascunse secrete capitale din toata matematica".

Bibliografie:

"Descoperirea in matematica" Gheorghe Polya, Editura Stiintifica Bucuresti 1971

Anexa 1

Anexa 2

Anexa 3