STRUCTURI DE DATE DINAMICE IN ALOCARE STATICA

STRUCTURI DE DATE DINAMICE

IN ALOCARE STATICA

In practica programarii exista multe probleme care presupun structuri ale informatiei mult mai complicate, a caror caracteristica principala este aceea ca se modifica structural in timpul executiei programului. Rezultand o modificare dinamica atat a formei, cat si a dimensiunii lor, aceste structuri de date se numesc dinamice.

In continuare vor fi prezentate doua tipuri de structuri dinamice:

Structura de tip coada, respectiv structura de tip stiva.

COADA (FIRUL DE ASTEPTARE)

Un principiu de gestionare a listelor simplu inlantuite este principiul FIFO (First In First Out). Conform acestui principiu, primul element introdus in lista este si primul care este scos din lista.

Despre o lista gestionata in acest fel se spune ca formeaza o coada. Cele doua capete ale listei simplu inlantuite care implementeaza o coada sunt capetele cozii.

Asupra cozilor se definesc trei operatii:

a.       Adaugarea unui element in coada;

b.      Scoaterea unui element din coada;

c.       Stergerea (vidarea) unei cozi.

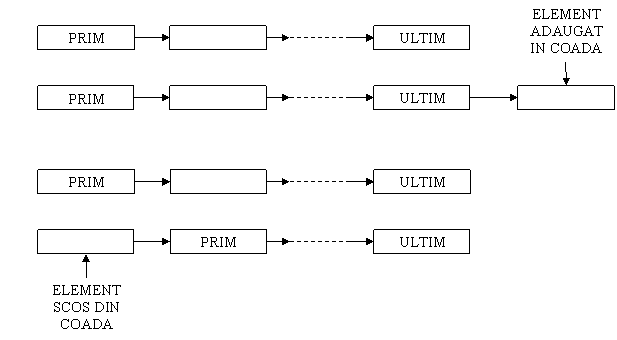
Cozile definite ca mai sus corespund celor din viata de toate zilele si din aceasta cauza ele se folosesc frecvent in probleme de simulare a fenomenelor reale.

STIVA

O stiva este o lista simplu inlantuita gestionata conform principiului LIFO (Last In First Out).

Conform acestui principiu, ultimul nod pus in stiva este primul nod care este scos din stiva.

Stiva, ca si lista, are doua capete: baza stivei si varful stivei.

Asupra unei stive se definesc cateva operatii, dintre care cele mai importante sunt:

1. Adaugarea unui element pe stiva;

2. Scoaterea unui element din stiva;

3. Stergerea (vidarea) stivei.

Primele doua operatii se realizeaza in varful stivei. Astfel, daca se scoate un element, atunci acesta este cel din varful stivei si in continuare, cel pus anterior lui ajunge in varful stivei, iar daca un element este adaugat pe stiva, atunci acesta se pune in varful stivei.

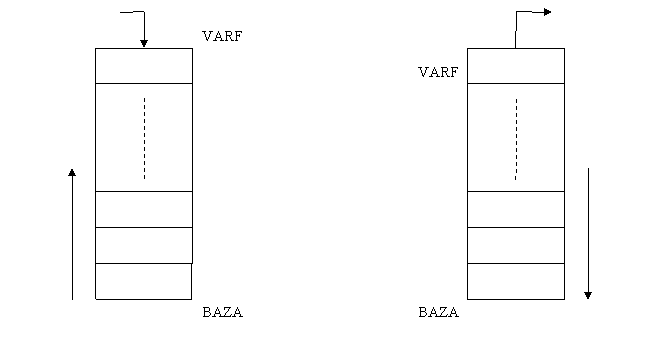
Intrarea unui element (stiva creste) Iesirea unui element (stiva scade)