Multimi poliedrale

Multimi poliedrale

Multimile poliedrale constituie in spatiu analogul suprafetelor poligonale din plan, cu deosebirea ca in acest caz suprafetele poligonale convexe sunt inlocuite cu prisme , piramide si trunchiuri de piramida.

Definitie : Se numeste multime poliedrala , o multime de puncte din spatiu care este reuniunea unui numar finit de prisme, piramide si trunchiuri de piramida, acestea avand doua cate doua interioarele disjuncte.

In acest caz, daca P este o multime poliedrala , iar P_1, P_{2, . ,} P_n sunt prisme, piramide si trunchiurile de piramida respective, adica P = P₁ P₂ P_n, si Int P_i Int P_j= , i≠j, atunci se va spune ca multimea P se descompune in multimile P_1, P_{2, . ,} P_n.

Un punct O al multimii poliedrale P se numeste punct interior al lui P daca exista un corp sferic cu centrul in O inclus in P. Punctele multimii P ce nu sunt puncte interioare acesteia se numesc puncte de frontiera. Aceasta definitie a punctului interior unei multimi poliedrale reprezinta analogul punctului de acumulare al unei multimi de numere , din analiza matematica, cu deosebirea ca in acest caz a fost inlocuit intervalul centrat in O , cu sfera avand centrul in O.

Exemple

Punctele din interiorul unei prisme , piramide sau trunchi de piramida sunt puncte interioare acestei multimi . Intr-adevar , pentru un punct O din interiorul acestei multimi se noteaza cu r numarul strict pozitiv mai mic decat toate distantele de la O la fetele prismei, piramidei sau trunchiului de piramida din care face parte . Atunci corpul sferic de centru O si raza r este evident inclus in multimea respectiva.

Se considera cubul [ABCDA'B'C'D'] si piramida [VBCC'] unde BI(AV). ( vezi fig. 9). Pe multimea poliedrala formata din reuniunea cubului cu piramida , punctele interioare multimii poliedrale sunt punctele interioare ale cubului si piramidei, pus punctele din Int BCC'.

In baza exemplului 1. Putem defini interiorul acestei multimi poliedrale oarecare P ca fiind multimea punctelor interioare ale lui P. multimea punctelor de frontiera ale lui P se numeste frontiera lui P

In continuare vom stabili o descompunere a multimilor poliedrale in analoga descompunerii suprafetelor poligonale in plan. Asadar daca in plan orice suprafata poligonala se descompune in suprafete triunghiulare in spatiu este adevarata urmatoarea

Teorema : Orice multime poliedrala se poate descompune in tetraedre.

Demonstratia rezulta din urmatoarele proprietati de descompunere a prismelor , piramidelor si trunchiurilor de piramida.

Proprietatea 1. Orice prisma se descompune in prisme triunghiulare.

Demonstratie

Se considera prisma P de baze S si S'. Stim ca suprafata poligonala S se descompune in suprafetele triunghiulare T₁, T₂, T₃, . , T_m. Prismele determinate de bazele T₁, T₂, T₃, . , T_m , planul bazei S' si avand muchiile paralele cu muchiile laterale ale prismei P, au interioarele disjuncte si reuniunea lor coincide cu P. (vezi fig.10).

Proprietatea 2 Orice prisma triunghiulara se descompune in trei tetraedre.

Demonstratie

Se considera prisma P=[ABCA'B'C'] si piramidele P₁=[A'ABC'], P₂=[BB'CA'] si P₃=[B'C'A'C]. Cele trei piramide au interioarele disjuncte deoarece oricare doua au ca intersectie o fata sau o muchie, iar reuniunea lor este P.( vezi fig 11), deci P se descompune in P₁, P₂, P₃.

Proprietatea 3 Orice piramida se descompune in piramide triunghiulare.

Demonstratie

Proprietatea rezulta din faptul ca baza piramidei se descompune in suprafete triunghiulare cu interioarele disjuncte care impreuna cu varful piramidei determina piramidele ce realizeaza descompunerea ( vezi fig. 12).

Proprietatea 4 Orice trunchi de piramida se descompune in trunchiuri de piramida triunghiulara.

Demonstratie

Proprietatea este o consecinta imediata a proprietatii 3.( a se vedea fig 13).

Proprietatea 5 Orice trunchi de piramida triunghiulara se descompune in trei tetraedre.

Demonstratie

Descompunerea este analoga celei din proprietatea 2( fig 14).

Vom admite urmatoarea proprietate:

Daca doua multimi poliedrale sunt congruente si una din ele este descompusa in tetraedrele T₁, T₂, T₃, . , T_n, atunci si cealalta poate fi descompusa in tetraedrele T'₁, T'₂, T'₃, . , T'_n, astfel ca T_i= T'_i,i= , nIN.

Un corespondent in spatiu al suprafetelor poligonale cu frontiera poligon il constituie poliedrele.

Definitie : O multime poliedrala P se numeste poliedru daca are urmatoarele proprietati:

Pentru oricare doua puncte interioare ale lui P exista o linie poligonala cu extremitatile in cele doua puncte , formata numai din puncte interioare;

Pentru oricare doua puncte care nu apartin lui P exista o linie poligonala cu extremitatile in cele doua puncte , formata numai din puncte care nu apartin lui P

Exemple si contraexemple:

Reuniunea dintre o prisma si o piramida care au ca intersectie o suprafata poligonala este un poliedru.

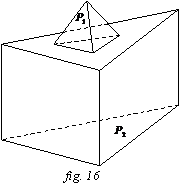Reuniunea a doua prisme care au ca intersectie o muchie nu este poliedru.

Se considera cubul [ABCDA'B'C'D'] de latura a si O centrul sau ( intersectia diagonalelor). Piramidele cu varful in O si avand ca baze fetele cubului se sectioneaza cu plane paralele cu bazele situate la distanta de baze. Reuniunea trunchiurilor de piramida astfel formate nu este poliedru.

Definitii : Se numeste varf al unui poliedru , un punct ce apartine frontierei poliedrului si nu apartine niciunui segment inclus in frontiera.

Se numeste muchie a unui poliedru un segment determinat de doua varfuri ale poliedrului, inclus in frontiera si ale carui puncte nu apartin interiorului niciunei suprafete poligonale inclusa in frontiera.

Un poliedru se numeste convex daca este o multime convexa. Acceptam in mod intuitiv , ca in cazul unui poliedru convex, frontiera este o reuniune de suprafete poligonale convexe ale caror laturi sunt muchiile ale poliedrului. O astfel de suprafata poligonala convexa se numeste fata a poliedrului.