 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Matematici financiare si actuariale - test grila
Evenimentul sigur:
|
a. |
apare sau se realiza obligatoriu sau in mod necesar odata cu oricare dintre rezultatele experimentului considerat; |
|
b. |
nu poate sa apara in nici un rezultat al experimentului considerat; |
|
c. |
poate sa apara sau sa nu apara odata cu un rezultat al experimentului considerat; |
|
d. |
nu exista |
R: A
2. Dintr-un lot de produse se extrag simultan patru produse. Notam cu A evenimentul ca toate cele patru produse extrase sa fie bune si cu B evenimentul ca cel putin unul sa fie necorespunzator. Atunci:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
3. Probabilitatea evenimentului A conditionata de evenimentul B este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
4. Dintr-un lot de 100 de piese din care 6 piese au defecte remediabile, 4 piese sunt rebuturi, iar restul sunt bune se iau 10 piese la intamplare. Probabilitatea evenimentultu ca din acestea 7 sa fie bune, 2 cu defecte remediabile si 1 sa fie rebut este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
5. Variabila
aleatoare ![]() este continua
daca
este continua
daca
|
a. |
multimea valorilor pe care le ia este o multime finita sau cel mult numarabila; |
|
b. |
multimea valorilor pe care le ia este multimea vida; |
|
c. |
multimea valorilor pe
care le ia este multimea |
|
d. |
multimea valorilor pe care le ia este un interval sau o reuniune de intervale. |
R: D
6. Fie X o variabila aleatoare. Dispersia variabilei X este:
|
a. |
momentul initial de ordinul doi; |
|
b. |
momentul centrat de ordinul doi; |
|
c. |
media variabilei aleatoare |
|
d. |
|
R: C
7. Pentru a cerceta prezenta studentilor la un anumit curs s-a ales un esantion de n studenti si s-a inregistrat numarul absentelor acestora la patru cursuri consecutive:
|
Nr. Studenti | |||||
|
Nr. Absenti |
Media si dispersia de selectie sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
8. Forma matriceala a grafului ![]()
![]() si
si ![]() este:
este:
|
a. |
|
c. |
|
|
b. |
|
d. |
|
R: A
9. Drumul
de valoare maxima intre varfurile ![]() si
si ![]() ,
ale unui graf, cunoscand distantele,
,
ale unui graf, cunoscand distantele, ![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
10. Care este dobanda simpla aferenta plasarii sumei
de ![]() u.m.
pe o durata de 72 de zile cu un procent anual de 8%?
u.m.
pe o durata de 72 de zile cu un procent anual de 8%?
|
a. |
80 u.m.; |
|
b. |
160 u.m.; |
|
c. |
200 u.m.; |
|
d. |
800 u.m. |
R: B
Diferenta a doua
capitaluri ![]() si
si ![]() este 12000 u.m. Cel mai mare
capital este plasat 8 luni cu 5%, iar celalalt 5 luni cu 4%. Dobanda
simpla obtinuta este de 1300 u.m. Cele doua capitaluri
sunt:
este 12000 u.m. Cel mai mare
capital este plasat 8 luni cu 5%, iar celalalt 5 luni cu 4%. Dobanda
simpla obtinuta este de 1300 u.m. Cele doua capitaluri
sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
12. O firma planifica sa investeasca o
suma de bani la inceputul fiecarui an, pentru a acumula o suma
de ![]() u.m. la sfarsitul
perioadei de 5 ani. Care este
valoarea acestei sume, daca rata investitiei este 14%?
u.m. la sfarsitul
perioadei de 5 ani. Care este
valoarea acestei sume, daca rata investitiei este 14%?
|
a. |
13608,22 u.m.; |
|
b. |
13850,78 u.m.; |
|
c. |
14000 u.m.; |
|
d. |
13270,52 u.m |
R: D
13. Suma de 8000 u.m. plasata timp de 3 ani in regim de dobanda compusa cu procentele anuale consecutive de 3%, 4% si 5% devine:
|
a. |
8468,17 u.m.; |
|
b. |
8500 u.m.; |
|
c. |
8867,05 u.m.; |
|
d. |
8998,08 u.m. |
R: D
14. Patru sume in progresie aritmetica sunt plasate 10 luni cu dobanda simpla, cu un procent anual de 9%. Dobanda totala este de 1200 u.m. iar diferenta dintre a 4-a suma si prima suma este de 6000 u.m. Cele patru sume sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
15. Daca
![]() este variabila
aleatoare ce reprezinta plata despagubirii si
este variabila
aleatoare ce reprezinta plata despagubirii si ![]() variabila
aleatoare ce reprezinta achitarea primei, se spune ca
operatiunea financiara de asigurare este echitabila daca:
variabila
aleatoare ce reprezinta achitarea primei, se spune ca
operatiunea financiara de asigurare este echitabila daca:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
16. Evenimentul imposibil:
|
a. |
apare sau se realiza obligatoriu sau in mod necesar odata cu oricare dintre rezultatele experimentului considerat; |
|
b. |
nu poate sa apara in nici un rezultat al experimentului considerat; |
|
c. |
poate sa apara sau sa nu apara odata cu un rezultat al experimentului considerat; |
|
d. |
nu exista. |
R: B
17. Un om de afaceri incheie intr-o zi trei afaceri care pot
fi rentabile (![]() ) sau nerentabile (
) sau nerentabile (![]() )i=1,2,3, in final.
Evenimentul corespunzator situatiei in care una din afacerile
incheiate este rentabila este:
)i=1,2,3, in final.
Evenimentul corespunzator situatiei in care una din afacerile
incheiate este rentabila este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
18. Un aparat se compune din 3 dispozitive care se pot defecta
independent unul de altul. Un singur defect este
suficient ca aparatul sa nu functioneze. Probabilitatea de
functionare fara defect a primului dispozitiv este 0 , a celui de-al doilea este 0,7 si a celui de-al
treilea 0,6. Notand
cu ![]() probabilitatea ca dispozitivul
i sa functioneze putem afirma ca aparatul functioneaza
cu probabilitatea:
probabilitatea ca dispozitivul
i sa functioneze putem afirma ca aparatul functioneaza
cu probabilitatea:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
19. Se arunca un zar de 10 ori. Probabilitatea de a obtine de 3 ori fata 6, de 2 ori fata 1 si de 4 ori fata 2 este:
|
a. |
|
c. |
|
|
b. |
|
d. |
|
R: C
20. Daca X este o variabila aleatoare cu
functia de repartitie F(x) atunci pentru orice numere reale ![]() date avem intotdeauna:
date avem intotdeauna:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
Daca densitatea de
repartitie a unei variabile aleatoare este 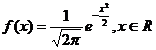 atunci:
atunci:
|
a. |
nu putem determina extremele
lui |
|
b. |
|
|
c. |
|
|
d. |
|
R: C
22. Forma matriceala a grafului ![]()
![]() si
si ![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
23. Drumul
de valoare maxima intre varfurile ![]() si
si ![]() ,
ale unui graf, cunoscand distantele
,
ale unui graf, cunoscand distantele ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
24. Incepand cu data de 1 ianuarie o persoana plaseaza la fiecare intai ale lunii cate 1500 u.m. cu un procent anual de 5% timp de un an de zile. Pe 31 decembrie isi retrage toti banii depusi. Dobanda simpla aferenta acestei operatiuni financiare este:
|
a. |
487,5 u.m.; |
|
b. |
503,7 u.m.; |
|
c. |
398,2 u.m.; |
|
d. |
490,5 u.m. |
R: A
25. Suma investita in regim de dobanda compusa cu 12%, acumulandu-se dupa 3 ani 4917,25 u.m. este:
|
a. |
4000 u.m.; |
|
b. |
3500 u.m.; |
|
c. |
4100 u.m.; |
|
d. |
3900 u.m. |
R: B
26. Depunand a suma de 500000 u.m. se achita doua datorii care erau una de 100000 u.m. acum 15 luni si cealalta de 200000 u.m. acum 4 luni. Capitalizarea facandu-se cu dobanda simpla, rata anuala de dobanda este:
|
a. |
p=22%.; |
|
b. |
p=30%.; |
|
c. |
p= 19%.; |
|
d. |
p= 48%. |
R: D
27. Se plaseaza suma de 15000 u.m. in regim de dobanda compusa timp de 5 ani. Dobanda aferenta acestei sume daca procentele anuale sunt respectiv egale cu 3%, 4%, 5%, 6% si 7% este:
|
a. |
4681,1475 u.m.; |
|
b. |
4135,5419 u.m.; |
|
c. |
4670,5023 u.m.; |
|
d. |
u.m. |
R: B
Daca cineva ne ofera 1000 u.m. peste 5 ani, cati bani ar trebui sa-i dam acum, corespunzator unei rate a dobanzii compuse de 6%?
|
a. |
747,38 u.m.; |
|
b. |
745 u.m.; |
|
c. |
698,45 u.m.; |
|
d. |
u.m. |
R: A
29. O banca emite certificate in valoare de 5000 u.m. cu termen la 5 ani si la o rata a dobanzii de 6,75% compusa semi-anual. O alta banca se poate face acelasi depozit la o rata anuala a dobanzii de 6,5% compusa lunar. Diferenta intre sumele de bani castigate este:
|
a. |
102,567 u.m.; |
|
b. |
98,0602 u.m.; |
|
c. |
91,3075 u.m.; |
|
d. |
99,89761 u.m |
R: C
30. Fie A o asigurare de persoane compusa din m
asigurari partiale ![]() carora le corespund primele
carora le corespund primele ![]() pentru acelasi asigurat.
Daca P este prima unica a asigurarii A atunci avem:
pentru acelasi asigurat.
Daca P este prima unica a asigurarii A atunci avem:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
31. Un eveniment este elementar daca:
|
a. |
apare ca un rezultat al experimentului considerat si numai cu unul; |
|
b. |
apare cu doua sau mai multe rezultate ale experimentului considerat; |
|
c. |
este notat cu o litera mare a alfabetului; |
|
d. |
are exact trei rezultate ale experimentului considerat. |
R: A
Un student solicita o
bursa de studii de la trei banci care obisnuiesc sa acorde
astfel de credite. Dupa studierea dosarului depus pentru creditare, acesta
poate primi raspunsul Da sau Nu. Se noteaza cu ![]() evenimentul corespunzator unui
raspuns favorabil de la banca i, i=1,2,3, respectiv
evenimentul corespunzator unui
raspuns favorabil de la banca i, i=1,2,3, respectiv ![]() evenimentul corespunzator unui
raspuns nefavorabil de la aceeasi banca. Atunci, faptul ca nu a primit nici un
raspuns favorabil poate fi exprimat astfel:
evenimentul corespunzator unui
raspuns nefavorabil de la aceeasi banca. Atunci, faptul ca nu a primit nici un
raspuns favorabil poate fi exprimat astfel:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
33. O grupa de studenti din anul I are de realizat
trei lucrari de cercetare. In ipoteza ca cele trei proiecte pot fi
integral realizate cu probabilitatile ![]()
![]() si
si ![]() probabilitatea ca cel
putin un proiect sa fie terminat la timp este:
probabilitatea ca cel
putin un proiect sa fie terminat la timp este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
34. Se urmareste importul a trei tipuri de produse
si se verifica, prin alegerea la intamplare a unui produs din fiecare
tip, o caracteristica specifica. Primul produs corespunde cu
probabilitatea ![]() , al doilea cu
, al doilea cu ![]() si al treilea cu
si al treilea cu ![]() Probabilitatea ca toate trei sa fie
corespunzatoare este:
Probabilitatea ca toate trei sa fie
corespunzatoare este:
|
a. |
P=0,73; |
|
b. |
P=1; |
|
c. |
P=0,564; |
|
d. |
P=0,684. |
R: D
35. Constantele reale a si b pentru care functia ![]() este functie densitate de
probabilitate sunt:
este functie densitate de
probabilitate sunt:
|
a. |
a=1, b=-1; |
|
b. |
a=-1, b=1; |
|
c. |
a=0, b=2; |
|
d. |
a=2, b=-1; |
R: A
36. Distributia variabilei aleatoare X este ![]() . Probabilitatea ca variabila
X sa ia o valoare mai mica sau egala cu 3 este:
. Probabilitatea ca variabila
X sa ia o valoare mai mica sau egala cu 3 este:
|
a. |
P=1/4; |
|
b. |
P=7/4; |
|
c. |
P=5/6; |
|
d. |
P=1. |
R: A
Forma analitica a grafului G, a carui matrice booleana este
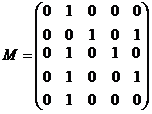 este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
38. Graful
atasat unui proiect, prezentand succesiunea operatiilor si
durata acestora in zile este dat de ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Timpul minim de finalizare a proiectului este:
.
Timpul minim de finalizare a proiectului este:
|
a. |
11 zile; |
|
b. |
19 zile; |
|
c. |
32 zile; |
|
d. |
35 zile. |
R: C
39. Suma
care a fost plasata cu dobanda simpla pe data de 15 ianuarie cu
procentul anual de 5% astfel incat pe 20 septembrie acelasi an suma
cumulata sa fie ![]() este:
este:
|
a. |
9500 u.m.; |
|
b. |
9625,20 u.m.; |
|
c. |
9671,17 u.m.; |
|
d. |
9302,5 u.m. |
R: C
40. Rata dobanzii care este necesara pentru ca 20000 u.m. sa devina 50000 u.m. in 12 ani este:
|
a. |
p=12%.; |
|
b. |
p=10%.; |
|
c. |
p= 9%.; |
|
d. |
p= 8%. |
R: D
41. Diferenta dintre doua capitaluri este de 35000 u.m.Cel mai mare a fost plasat 6 luni cu 5%, iar al doilea 4 luni cu 6% conducand la o dobanda simpla totala in valoare de 2000 u.m.Cele doua capitaluri sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
42. Suma care in 40 de zile produce o dobanda egala cu suma dobanzillor produse de: 600 u.m. pe timp de 90 de zile si 1000 u.m.pe timp de 60 de zile este:
|
a. |
2850 u.m.; |
|
b. |
3850 u.m.; |
|
c. |
4300 u.m.; |
|
d. |
2327 u.m. |
R: A
Sa presupunem ca primiti o carte de credit pentru care rata dobanzii lunare este de 3%. Care este de fapt rata dobanzii anuale care vi se aplica?
|
a. | |
|
b. | |
|
c. | |
|
d. |
%. |
R: B
44. Ce suma trebuie investita la 31 ianuarie pentru a avea 7700 u.m. la 18 august, acelasi an, daca investitia se face la o rata anuala a dobanzii de 10%?
|
a. |
7301,90 u.m.; |
|
b. |
7300 u.m.; |
|
c. |
6998,90 u.m.; |
|
d. |
7051,17u.m |
R: A
45. Fie A evenimentul ca o persoana aleasa la intamplare dintr-o populatie in varsta de x ani sa fie in viata la implinirea varstei de (x+1) ani. Probabilitatea de viata este data de:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
46. Evenimentele A si B sunt compatibile daca:
|
a. |
realizarea lor simultana este imposibila; |
|
b. |
realizarea lor simultana este posibila; |
|
c. |
realizarea unuia consta din nerealizarea celuilalt; |
|
d. |
evenimentul B se realizeaza ori de cate ori se realizeaza evenimentul A. |
R: B
47. Un lot de produse ambalate in cutii, oferite de o
firma este acceptat de beneficiar, daca in urma examinarii a 5
cutii extrase la intamplare, continutul lor se constata
corespunzator. Notand cu ![]() evenimentul corespunzator
situatiei ca la examinarea cutiei cu numarul i,
evenimentul corespunzator
situatiei ca la examinarea cutiei cu numarul i, ![]() continutul este
corespunzator, faptul ca dupa examinarea a trei cutii extrase la
intamplare, lotul a fost respins poate fi exprimat astfel:
continutul este
corespunzator, faptul ca dupa examinarea a trei cutii extrase la
intamplare, lotul a fost respins poate fi exprimat astfel:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
48. O societate comerciala apeleaza la 3
experti ![]()
![]() pentru a oferi solutii viabile de
rentabilizare. Din datele statistice se stie ca expertii
pentru a oferi solutii viabile de
rentabilizare. Din datele statistice se stie ca expertii ![]() ofera solutii
viabile cu probabilitatile 0,8; 0,7 si 0,6 respectiv.
Probabilitatea ca toti sa ofere solutii viabile este:
ofera solutii
viabile cu probabilitatile 0,8; 0,7 si 0,6 respectiv.
Probabilitatea ca toti sa ofere solutii viabile este:
|
a. |
p=0,336; |
|
b. |
p=0,976; |
|
c. |
p=0,452; |
|
d. |
p=0,73. |
R: A
49. Dintr-un lot de 100 de piesedin care 6 piese au defecte remediabile, 4 piese sunt rebuturi, iar restul sunt bune se iau 10 piese la intamplare. Probabilitatea evenimentultu ca din acestea 7 sa fie bune, 2 cu defecte remediabile si 1 sa fie rebut este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
50. Fie data variabila aleatoare discreta X. Valoarea medie a acesteia are axpresia:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
51. Distributia variabilei aleatoare X este ![]() . Atunci valoarea lui q este:
. Atunci valoarea lui q este:
|
a. |
q=1/3; |
|
b. |
q=2/5; |
|
c. |
q=-2; |
|
d. |
q=3/2. |
R: B
Drumul de valoare minima
intre varfurile ![]() si
si ![]() , ale unui graf, cunoscand
distantele,
, ale unui graf, cunoscand
distantele, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
53. Pentru
a organiza trRportul postei prin 5 localitati notate cu ![]() se
incearca folosirea posibilitatilor de trRport reprezentate prin
arce astfel:
se
incearca folosirea posibilitatilor de trRport reprezentate prin
arce astfel: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Este posibila trecerea prin toate cele 5
localitati cate o singura data? In caz afirmativ in ce ordine trebuie parcurse?
.
Este posibila trecerea prin toate cele 5
localitati cate o singura data? In caz afirmativ in ce ordine trebuie parcurse?
|
a. |
Nu. |
|
b. |
Da. |
|
c. |
Da. |
|
d. |
Da. |
R: B
54. Cu ce procent trebuie plasata suma de 1500 u.m. timp de 4 luni cu dobanda simpla, pentru ca suma finala sa fie 2000 u.m.?
|
a. |
p=8%.; |
|
b. |
p=80%.; |
|
c. |
p=50%.; |
|
d. |
p=100%. |
R: D
55. Care este suma acumulata dupa un an daca se investesc 100 u.m. cu o rata a dobanzii de 12% compusa trimestrial?
|
a. |
110 u.m.; |
|
b. |
115 u.m.; |
|
c. |
112,55 u.m.; |
|
d. |
112 u.m. |
R: C
56. Doua capitaluri a caror suma este de 40000 u.m. sunt plasate cu dobanda simpla astfel: primul 60 de zile cu 4%, iar al doilea 80 de zile cu 6%. Dobanda primului este dublul dobanzii celui de-al doilea. Cele doua capitaluri sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
57. Suma initiala care va trebui depusa pentru a acumula 1100 u.m. dupa 3 ani stiind ca s-a folosit o rata a dobanzii compuse de 6% este:
|
a. |
885,0231 u.m.; |
|
b. |
938,5045 u.m.; |
|
c. |
923,5936 u.m.; |
|
d. |
972,7886 u.m. |
R: C
58. Care este valoarea finala a unei investitii de 15000 u.m.peste 4 ani, la o rata a dobanzii compuse semi-anuale de 9,5%?
|
a. |
21321,6568u.m.; |
|
b. |
22761,8970 u.m.; |
|
c. |
21741,9153 u.m.; |
|
d. |
20998,8751 u.m. |
R: C
59. Diferenta dintre doua capitaluri ![]() si
si ![]() este de 12000 u.m.Cel mai mare
capital este plasat 8 luni cu 5%, iar celalalt 5 luni cu 4%. Dobanda
simpla totala obtinuta este de 1300 u.m. Cele doua
capitaluri sunt:
este de 12000 u.m.Cel mai mare
capital este plasat 8 luni cu 5%, iar celalalt 5 luni cu 4%. Dobanda
simpla totala obtinuta este de 1300 u.m. Cele doua
capitaluri sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
60. Fie A evenimentul ca o persoana aleasa la intamplare dintr-o populatie in varsta de x ani sa fie in viata la implinirea varstei de (x+1) ani. Probabilitatea de moarte este data de:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
61. O societate comerciala realizeaza in cursul unui an 4 tipuri de produse.In fiecare luna realizeaza, in functie de cererea de pe piata unul sau mai multe dintre aceste tipuri de produse. Campul de evenimente asociat productiei unei luni este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
62. Probabilitatea de realizare a evenimentului A este:
|
a. |
raportul dintre numarul
de cazuri posibilr si numarul de cazuri favorabile |
|
b. |
un eveniment favorabil realizarii evenimentului A; |
|
c. |
o functie |
|
d. |
masura sRei de realizare a evenimentului A. |
R: D
Intr-o cutie sunt 15 piese asemanatoare ca forma, dar 6 sunt cu defecte. Se scot trei piese fara a le returna an cutie. Probabilitatea ca cele trei piese sa fie fara defect este:
|
a. |
p=0,6; |
|
b. |
p=0,76; |
|
c. |
p=0,18; |
|
d. |
p=0,32. |
R: C
Fie X o variabila aleatoare. Se numeste mediana a acesteia un numar cu proprietatea:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
Fie variabila aleatoare ![]() . Media sa este:
. Media sa este:
|
a. |
M(X)=5,1; |
|
b. |
M(X)=0,1; |
|
c. |
M(X)=7,2; |
|
d. |
M(X)=4,6. |
R: D
66. Pentru variabila aleatoare X cu functia densitate de
probabilitate ![]() , media M(X) este:
, media M(X) este:
|
a. | |
|
b. | |
|
c. | |
|
d. |
R: B
67. Drumul de valoare minima intre varfurile ![]() si
si ![]() , ale unui graf, cunoscand
distantele
, ale unui graf, cunoscand
distantele ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: D
68. Drumul
hamiltonian in graful ![]()
![]() a
cu matricea booleana
a
cu matricea booleana 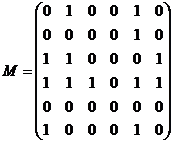 este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: A
Pe ce durata ar trebui plasata, in regim de dobanda simpla suma de 2000 u.m., cu procentul anual de 6%, pentru a obtine o dobanda de 360 u.m.?
|
a. |
2 ani; |
|
b. |
1 an si 6 luni; |
|
c. |
3 ani; |
|
d. |
4 ani. |
R: C
70. O intreprindere va trebui sa cheltuiasca 300000 u.m. pentru un nou utilaj peste doi ani. In perioada curenta, rata nomonala anuala a investitiilor de capital este de 10%. Ce suma unica ar trebui investita acum, daca compunerea se realizeaza semestrial?
|
a. |
246810,75 u.m.; |
|
b. |
250000 u.m.; |
|
c. |
246700,50 u.m.; |
|
d. |
238000 u.m. |
R: A
71. Ce suma va trebui sa achite astazi o persoana pentru a putea scapa de plata a 10 anuitati anticipate a 5000 u.m. fiecare cu 3%?
|
a. |
50023,12 u.m.; |
|
b. |
49850,45 u.m.; |
|
c. |
42359,36 u.m.; |
|
d. |
43929,53 u.m. |
R: D
72. Care este valoarea actuala a unei investitii care va ajunge la 8000 u.m. peste 4 ani, lo o rata a dobanzii de 8% compusa trimestrial?
|
a. |
5219,976 u.m.; |
|
b. |
6109,224 u.m.; |
|
c. |
5987,065 u.m.; |
|
d. |
5828,354 u.m. |
R: D
73. Fie un imprumut in valoare de 300000 u.m. compus din doua parti care urmeaza sa se achite in regim de dobanda compusa cu un procent anual de 4%, peste 7 si respectiv 10 ani. Daca raportul valorilor finale este 5/3, imprumuturile sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
74. Ce rata a dobanzii simple trebuie aplicata pentru ca o investitie de 740 u.m. sa aduca o dobanda de 42,49 u.m. intre 10 iunie si 29 noiembrie, acelasi an?
|
a. | |
|
b. | |
|
c. | |
|
d. |
%. |
R: A
75. Daca
![]() este variabila
aleatoare ce reprezinta plata despagubirii si
este variabila
aleatoare ce reprezinta plata despagubirii si ![]() variabila
aleatoare ce reprezinta achitarea primei, se spune ca
operatiunea financiara de asigurare este echitabila daca:
variabila
aleatoare ce reprezinta achitarea primei, se spune ca
operatiunea financiara de asigurare este echitabila daca:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
76. Daca o experienta oarecare genereaza n evenimente elementare (incompatibile), atunci campul de evenimente corespunzator, are:
|
a. |
2n-1 elemente; |
|
b. |
2n+1 elemente; |
|
c. |
2n-2 elemente; |
|
d. |
2n elemente. |
R: D
77. Un graf este simetric, daca:
|
a. |
orice pereche de varfuri adiacente se leaga intr-o singura directie; |
|
b. |
orice pereche de varfuri este legata cel putin intr-o directie; |
|
c. |
oricare doua varfuri adiacente sunt legate prin doua arce orientate opus unul celuilalt; |
|
d. |
este un subgraf partial al grafului dat. |
R: C
Un graf este antisimetric, daca:
|
a. |
oricare doua varfuri adiacente sunt legate prin doua arce opus unul celuilalt; |
|
b. |
nu contine bucle si orice pereche de varfuri adiacente se leaga intr-o singura directie; |
|
c. |
orice pereche de varfuri este legata cel putin intr-o directie; |
|
d. |
este un graf partial al grafului dat. |
R: B
79. Un graf este conex daca:
|
a. |
este simetric; |
|
b. |
este antisimetric; |
|
c. |
pentru orice pereche x si y de varfuri distincte, exista un lant ce pleaca de la varful x la varful y; |
|
d. |
pentru orice pereche x si y de varfuri distincte, exista un drum ce pleaca de varfulla x la varful y. |
R: C
80. Fie un graf de ordinul n. Un drum este hamiltonian, daca:
|
a. |
nu trece de doua ori prin acelasi varf; |
|
b. |
nu trece de doua ori prin acelasi arc; |
|
c. |
are lungimea (numar de arce) n; |
|
d. |
trece prin toate varfurile grafului. |
R: D
81. Operatia de dobanda compusa aplicata
asupra unei sume de valoarea initiala S dupa t=n+![]() unitati de timp cu
un procent p, da pentru suma la sfarsitul periodei de timp,
valoarea:
unitati de timp cu
un procent p, da pentru suma la sfarsitul periodei de timp,
valoarea:
|
a. |
S(1+p)n(1+ |
|
b. |
S(1+i)n(1+ |
|
c. |
S(1+i)n(1+ |
|
d. |
S(1+i)q(1+im). |
R: C
Operatia de dobanda compusa aplicata asupra unei sume de valoare intiala S, dupa t unitati de timp ( t natural) cu un procent p da pentru suma la sfarsitul perioadei de timp valoarea:
|
a. |
S(1+p)t; |
|
b. |
Sptt; |
|
c. |
S(1+ip)t ,cu i=p/100; |
|
d. |
S(1+i)t , cu i=p/100. |
R: D
Ce suma va exista la o banca peste 6 ani daca se depune azi suma de 3000 u.m. in regim de dobanda compusa cu un prcent de 5% ( 1,056= 1,27628):
|
a. |
3825,34 u.m.; |
|
b. |
3828,84 u.m.; |
|
c. |
3820,32 u.m.; |
|
d. |
3828 u.m. |
R: B
Procentul in care suma de 10000 u.m. imprumutata in regim de dobanda simpla devine 11000 u. m. pe o perioada de 4 ani, este:
|
a. | |
|
b. | |
|
c. | |
|
d. |
%. |
R: C
85. Timpul in care suma de 10000 u.m. imprumutata in regim de dobanda simpla cu p=10% devine 13000 u.m., este:
|
a. |
3 ani; |
|
b. |
3,5 ani; |
|
c. |
2,5 ani; |
|
d. |
4 ani. |
R: A
Suma de 10000 u.m. imprumutata in regim de dobanda simpla cu p=8% pe o perioada de 2,5 ani, devine:
|
a. |
11500 u.m.; |
|
b. |
12000 u.m.; |
|
c. |
12500 u.m.: |
|
d. |
12400 u.m. |
R: B
87. Suma de 9000 u.m. depusa cu un procent de 6% a adus un venit de 498 u.m. Cat timp a fost depusa?
|
a. |
10 luni; |
|
b. |
35 saptamani; |
|
c. |
340 zile; |
|
d. |
332 zile; |
R: D
88. Fie A si B doua evenimente oarecare.Atunci:
|
a. |
|
|
b. |
P(A |
|
c. |
P(A |
|
d. |
P(A |
R: B
89. Daca A este un eveniment aleator, atunci evenimentul contrar evenimentului A, este:
|
a. |
nu exista aceasta notiune; |
|
b. |
evenimentul care se produce ori de cate ori nu se produce evenimentul A; |
|
c. |
evenimentul care se produce odata cu producerea evenimentului sigur; |
|
d. |
evenimentul dat de
relatia: A |
R: B
90. Fie A si B doua evenimente oarecare. Reuniunea lor este:
|
a. |
evenimentul care se produce fie cand se produce evenimentul A, fie cand se produce evenimentul B, fie cand se produc ambele evenimente A si B; |
|
b. |
evenimentul care se produce numai atunci cand se produce evenimentul A; |
|
c. |
evenimentul care se produce numai cand se produce evenimentul B; |
|
d. |
evenimentul care se produce odata cu producerea simultana a evenimentelor A si B. |
R: A
91. Forma analitica a grafului G, a carui matrice
booleana M=  este:
este:
|
a. |
G=(X,A), X= si A=; |
|
b. |
G=(X,A), X= si A=; |
|
c. |
G= si A=; |
|
d. |
G= si A=. |
R: A
Fie X o variabila
aleatoare cu densitatea 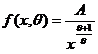
![]() . Atunci, valoarea lui A in
functie de
. Atunci, valoarea lui A in
functie de ![]() este:
este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: B
93. Dispersia
variabilei aleatoare ![]() este:
este:
|
a. | |
|
b. | |
|
c. | |
|
d. |
R: C
94. Incepand cu data de 1 ianuarie o persoana plaseaza la fiecare intai ale lunii cate 1500 u.m. cu un procent anual de 5% timp de un an de zile. Pe 31 decembrie isi retrage toti banii depusi. Dobanda simpla aferenta acestei operatiuni financiare este:
|
a. |
487,5 u.m.; |
|
b. |
503,7 u.m.; |
|
c. |
398,2 u.m.; |
|
d. |
490,5 u.m. |
R: A
95. Primiti 100 u.m. pe care ii puneti la banca. Banca va ofera dobanda compusa de 2% pe un an, timp de doi ani. Care este valoarea finala a acestei operatiuni?
|
a. |
121 u.m.; |
|
b. |
122 u.m.; |
|
c. |
125 u.m.; |
|
d. |
120 u.m. |
R: A
96. Care este valoarea finala a 34 u.m. dupa 5 ani, daca rata dobanzii compuse este de 5%?
|
a. |
45,67 u.m.; |
|
b. |
43,39 u.m.; |
|
c. |
42,31 u.m.; |
|
d. |
44,56 u.m. |
R: B
97. Fie un imprumut in valoare de 300000 u.m. compus din doua parti care urmeaza sa se achite in regim de dobanda compusa cu un procent anual de 4%, peste 7 si respectiv 10 ani. Daca raportul valorilor finale este 5/3, imprumuturile sunt:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
Fie o urna cu bile albe si negre cu p probabilitatea evenimentului de a extrage o bila neagra si q probabilitatea evenimentului contrar. Facandu-se n extractii succesive, introducandu-se de fiecare data bila extrasa in urna, atunci probabilitatea evenimentului ca din cele n bile extrase, k sa fie albe este (schema urnei cu bila revenita):
|
a. |
Cnkpn-kqk; |
|
b. |
Cknpkqn-k; |
|
c. |
pkqn-k; |
|
d. |
Cnkpkqn-k. |
R: D
Fie o urna cu a bile albe si b bile negre. Probabilitatea evenimentului ca luand deodata n bile, p bile sa fie albe si q bile sa fie negre- schema urnei cu bila nerevenita- este:
|
a. |
|
|
b. |
|
|
c. |
|
|
d. |
|
R: C
100. Care este dobanda adusa de suma de 4000 u.m. depusa la inceputul anului pe timp de un semestru cu rata dobanzii de 10% compusa trimestrial?
|
a. |
210 u.m.; |
|
b. |
202,75 u.m.; |
|
c. |
203,25 u.m.; |
|
d. |
202,50 u.m. |
R: D
101. Suma de 800 u.m. depusa pe timp de 300 dezilecu un procent de 6%, devine:
|
a. |
845 u.m.; |
|
b. |
840 u.m.; |
|
c. |
850 u.m.; |
|
d. |
839 u.m. |
R: B
102. Procentul platit pentru suma de 18000 u.m. pe timp de 5 luni daca dobanda a fost de 300 u.m., este:
|
a. | |
|
b. | |
|
c. | |
|
d. |
%. |
R: B
Copyright © 2024 - Toate drepturile rezervate