 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
METODA MULTIPLICATORILOR LUI LAGRANGE
Metoda multiplicatorilor lui Lagrange este o metoda, dezvoltata in analiza matematica, cu ajutorul careia se rezolva problemele de extrem cu legaturi. Prin urmare, aceasta metoda se poate folosi pentru determinarea valorilor unor necunoscute x1, x2, , xn care satisfac restrictiile de tip egalitate:
fi(x1, x2, , xn)=0, i=1, 2, , m
astfel incat o functie:
f=f(x1, x2, , xn )
sa capete valoarea minima sau valoarea maxima.
In metoda multiplicatorilor lui Lagrange se introduce functia:
L(x, )=f(x)-( 1f1(x)+ 2f2(x) + + mfm(x))
Aceasta functie este numita functia lui Lagrange iar 1, 2, , m sunt necunoscute numite multiplicatori ai lui Lagrange. Argumentul x care apare in definitia functiei lui Lagrange este vectorul care are drept componente necunoscutele x1, x2, , xn iar argumentul este vectorul care are drept componente multiplicatorii 1, 2, , m
Functiile f, fj j=1, 2, , m, care apar in problema, se presupun continue si cu derivatele partiale continue in raport cu fiecare din necunoscutele x1, x2, , xn. Se demonstreaza ca solutia optima a problemei trebuie sa satisfaca relatiile:
![]()
![]()
Aceste relatii formeaza un sistem de n+m ecuatii cu necunoscutele x1, x2, , xn, 1, 2, , m . Ele sunt coditii necesare pe care trebuie sa le satisfaca solutia optima. Daca functiile f, f1, f2, fm au o serie de proprietati suplimentate, atunci relatiile la care ne referim sunt si conditii suficiente.
Ca exemplu, consideram problEma in care se cere sa se determine valorile necunoscutelor x1 si x2 care satisfac restrictia:
(x1+3)2+(x2-3)2-1=0
astfel incat functia:
f(x1, x2)= (x1+2)2+(x2-2)2
sa capete valoarea maxima.
Pentru a rezolva aceasta problema, introducem functia lui Lagrange:
L(x1, x2, )= (x1+2)2+(x2-2)2- [(x1+3)2+(x2-3)2-1]
Prin urmare, solutia optima a problemei trebuie sa satisfaca sistemul de ecuatii:
x1- x1-3 +2=0
x2- x2+3 -2=0
(x1+3)2+(x2-3)2-1=0
Acest sistem de ecuatii are doua solutii. Ele sunt:
![]()
![]()
Cele doua solutii reprezinta punctele stationare ale functiei L.
Asa cum se stie din analiza matematica, un punct stationar este punct de maxim sau de minim daca diferentiala de ordin doi a functiei L este negativ definita sau, respectiv, pozitiv definita in punctul considerat. Mai reamintim, ca diferentiala de ordin doi a functiei L este:
![]()
unde Lij reprezinta derivatele partiale de ordin doi ale functiei L in raport cu xi si xj cu i=1, 2, j=1, 2.
In cazul nostru, diferentiala de ordin doi a functiei L este:
![]()
Este clar ca pentru:
![]()
diferentiala de ordin doi a lui L este negativ definita. Asadar, prima solutie a sistemului este solutia optima a problemei. Se constata usor ca valoarea optima a functiei obiectiv este:
![]()
Se mai observam ca pentru:
![]()
diferentiala de ordin doi a lui L este pozitiv definita. Prin urmare, a doua solutie a sistemului determina minimul functiei:
f(x1, x2)= (x1+2)2+(x2-2)2
cu restrictia:
(x1+3)2+(x2-3)2-1=0
In acest caz, valoarea optima a functiei este:
![]()
Rezultatele pe care le-am obtinut aici le putem gasi si pe cale grafica. In figura 6.2 apar doua curbe de nivel ale functiei obiectiv:
f(x1, x2)= (x1+2)2+(x2-2)2
Este vorba de cele doua cercuri care au centrul in punctul de coordonate (-2, 2). In aceeasi figura, apare si cercul corespunzator restrictiei:
(x1+3)2+(x2-3)2-1=0
Evident, este vorba de cercul cu centrul in punctul de coordonate (-3, 3) si raza egala cu 1.
Folosind figura 6.2, deducem ca solutia optima a problemei de maximizare pe care am formulat-o este data de coordonatele punctului situat la intersectia curbei de nivel f(x1, x2)=c1 cu cercul care are centrul in punctul de coordonate (-3, 3) si raza egala cu 1. Evident, pentru a determina solutia, trebuie sa calculam coordonatele punctului de tangenta dintre curba de nivel f(x1, x2)=c1 si cercul care reprezinta restrictia problemei. Sa observam ca punctul de tangenta dintre cele doua cercuri se afla pe dreapta care trece prin punctele de coordonate (-3, 2) si (-2, 2). Ecuatia acestei drepte este:
x1+x2=0
Desigur, coordonatele punctului de tangenta se obtin prin rezolvarea sistemului:
(x1+3)2+(x2-3)2-1=0
x1+x2=0
Acest sistem are solutiile:
![]()
si:
![]()
Este clar ca prima solutie reprezinta coordonatele punctului de tangenta dintre curba de nivel f(x1, x2)=c2 si cercul care reprezinta restrictia problemei. Daca introducem coordonatele solutiei optime in valoarea functiei obiectiv, deducem ca:
![]()
Figura 6.2 ne arata ca solutia pe care am calculat-o reprezinta un punct de maxim global.
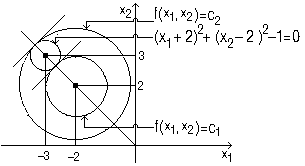
Fig. 6.2
Sa mai observam ca solutia a doua a sistemului de ecuatii reprezinta coordonatele punctului de tangenta dintre curba de nivel f(x1, x2)=c2 si cercul care reprezinta restrictia problemei. Prin urmare, coordonatele acestui punct ne dau solutia optima a problemei care cere sa se determine valorile necunoscutelor x1 si x2 care satisfac restrictia:
(x1+3)2+(x2-3)2-1=0
astfel incat functia:
f(x1,x2)= (x1+2)2+(x2-2)2
sa capete valoarea minima. Se constata usor ca:
![]()
Este clar ca punctul de minim pe care l-am determinat este un punct de minim global.
Copyright © 2024 - Toate drepturile rezervate